Giải sách bài tập Toán 12 nâng cao

Hãy chọn một phương án trong bốn phương án đã cho để được khẳng định đúng. Câu 4.38  Với mọi số ảo z, số \({z^2} + {\left| z \right|^2}\) là (A) Số thực dương                               (B) Số thực âm (C) Số 0                                              (D) Số ảo khác 0 Giải Chọn C ———————————————————- Câu 4.39  Nếu \(\left| z \right| = 1\) thì \({{{z^2} … [Đọc thêm...] vềÔn tập chương IV – Số phức – Giải SBT chương 4 Giải tích 12 nâng cao

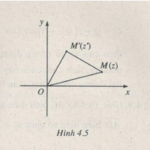
Bài 4.25 Cho hai số phức khác 0 là \(z = r\left( {{\rm{cos}}\varphi  + i\sin \varphi } \right)\) và \(z’ = r’\left( {{\rm{cos}}\varphi ‘ + i\sin \varphi ‘} \right),\left( {r,r’,\varphi ,\varphi ‘ \in R} \right)\) Tìm điều kiện cần và đủ về \(r,r’,\varphi ,\varphi ‘\) để \(z = z’\) Giải \(z = z’\) khi và chỉ khi hoặc \(r’ = r,\varphi ‘ = \varphi  + k2\pi \left( {k \in Z} … [Đọc thêm...] vềBài 3: Dạng lượng giác của số phức. Ứng dụng – Giải SBT chương 4 Giải tích 12 nâng cao

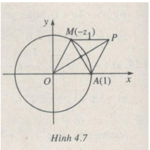
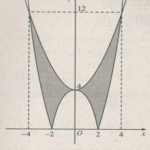
Bài 4.15 Hỏi khi số thức a thay đổi tùy ý thì các điểm của mặt phẳng phức biểu diễn các căn bậc hai của a + i vạch nên đường nào ? Giải Viết \(z = x + yi\left( {x,y \in R} \right)\) thì \({z^2} = a + i \Leftrightarrow \left\{ \matrix{{x^2} – {y^2} = a \hfill \cr 2xy = 1 \hfill \cr}  \right.\) Phương trình \(2xy = 1\) chứng tỏ điểm M biểu diễn z phải thuộc hypebol \(y … [Đọc thêm...] vềBài 2: Căn bậc hai của số phức, phương trình bậc hai – Giải SBT chương 4 Giải tích 12 nâng cao

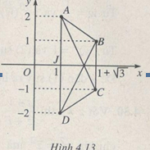
Bài 4.4 a) Các điểm A, B, C và A’, B’, C’ trong mặt phẳng phức theo thứ tự biểu diễn các số \(1 – i\),                   \(2 + 3i\),                   \(3 + i\)  và   \(3i\),          \(3 – 2i\),                 \(3 + 2i\)      Chứng minh rằng hai tam giác ABC và A’B’C’ có cùng trọng tâm. b) Biết các số phức \({z_1},{z_2},{z_3}\) biểu diễn bởi ba đỉnh nào đó của một … [Đọc thêm...] vềBài 1: Số phức – Giải SBT chương 4 Giải tích 12 nâng cao

Hãy chọn một trong bốn phương án đã cho để được khẳng định đúng. Câu 3.55  (A) \(f\left( x \right) = {e^{2x}}\)                 (B) \(f\left( x \right) = 2x{e^{{x^2}}}\)                (C) \(f\left( x \right) = {{{e^{{x^2}}}} \over {2x}}\)               (D) \(f\left( x \right) = {x^2}{e^{{x^2}}} – 1\) Giải Chọn B ————————————————————— Câu 3.56  Cho đồ thị hàm … [Đọc thêm...] vềÔn tập chương III – Nguyên hàm, tích phân và ứng dụng – Giải SBT chương 3 Giải tích 12 nâng cao

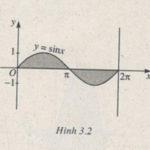
Bài 3.42 a) Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = \sin x\), trục hoành, trục tung và đường  thẳng \(x = 2\pi \)                                                   b) Tính diện tích hình phẳng giới hạn bởi các đồ thị hàm số \(y = 2 – x,y = {x^2}\) và trục hoành trong miền \(x \ge 0\) Giải a) Ta có  \(\sin x \ge 0\) trên đoạn \(\left[ {0 ;\pi } … [Đọc thêm...] vềBài: 5; 6. Một số ứng dụng hình học của tích phân – Giải SBT chương 3 Giải tích 12 nâng cao

Bài 3.38 a) Cho a > 0. Chứng minh rằng          \(\int\limits_\alpha ^\beta  {{{dx} \over {{x^2} + {a^2}}} = {1 \over a}\left( {r – k} \right)} \) trong đó r và k là các số thực thỏa mãn \({\rm{tan}}r = {\beta  \over a},\tan k = {\alpha  \over a}\) b) Tính \(\int\limits_0^{{\pi  \over 2}} {{{dx} \over {2 + c{\rm{os}}x}}} \)                           Giải a) Đặt … [Đọc thêm...] vềBài 4: Một số phương pháp tính tích phân – Giải SBT chương 3 Giải tích 12 nâng cao

Bài 3.20 Giả sử khi áp dụng công thức nguyên hàm từng phần, ta dẫn đến                \(\int {f\left( x \right)} dx = aG\left( x \right) – b\int {f\left( x \right)} dx\) Với \(b \ne 1\) Chứng minh rằng                                 \(\int {f\left( x \right)} dx = {{aG\left( x \right)} \over {b + 1}} + C\) với C là hằng số. Giải Ta có: \(\int {f\left( x … [Đọc thêm...] vềBài 2: Một số phương pháp tìm nguyên hàm – Giải SBT chương 3 Giải tích 12 nâng cao