Cho hình chóp tứ giác đều \(S.ABCD\) có cạnh đáy bằng \(a\), cạnh bên bằng \(a\sqrt 2 \). Độ lớn góc giữa đường thẳng \(SA\) và mặt phẳng đáy bằng

Cho hình chóp tứ giác đều \(S.ABCD\) có cạnh đáy bằng \(a\), cạnh bên bằng \(a\sqrt 2 \). Độ lớn góc giữa đường thẳng \(SA\) và mặt phẳng đáy bằng

A. \({45^ \circ }\).

B. \({75^ \circ }\).

C. \({30^ \circ }\).

D. \({60^ \circ }\).

Lời giải:

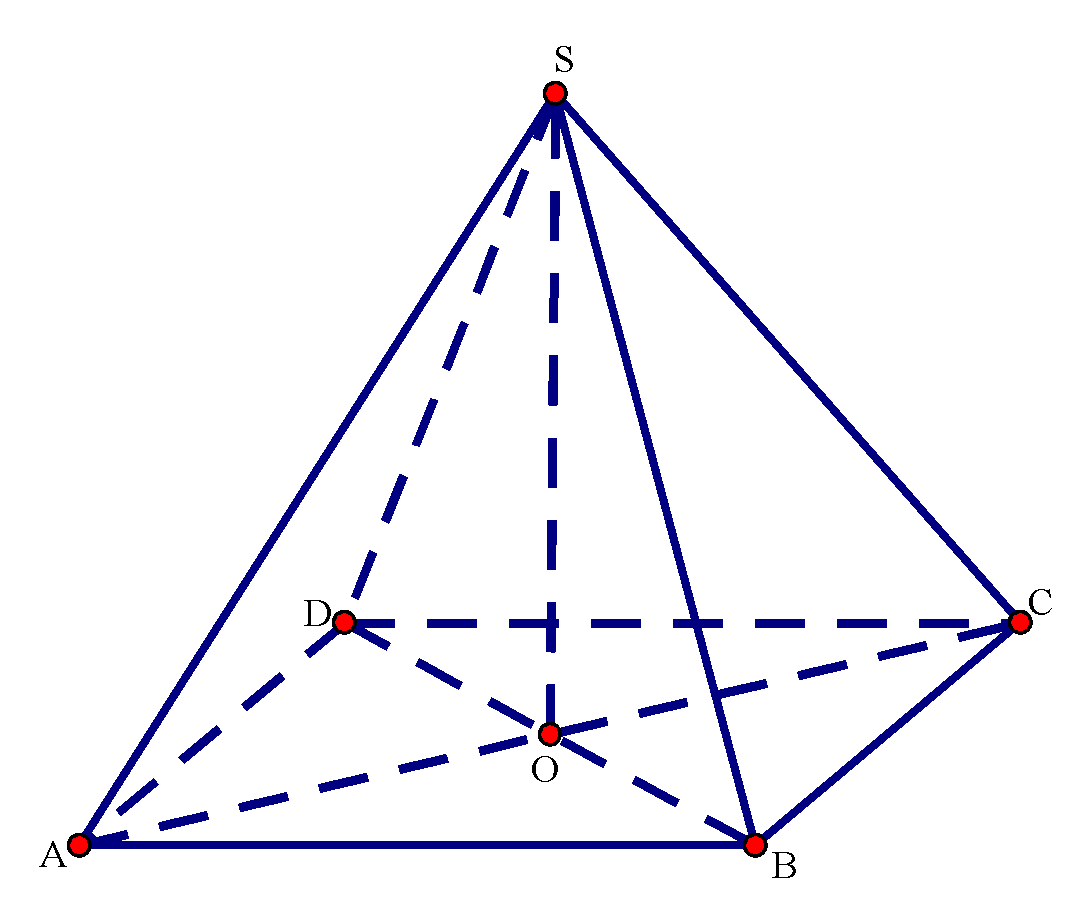
Gọi \(O\) là giao điểm của \(AC\) và \(BD\).

Vì hình chóp \(S.ABCD\) là hình chóp đều nên \(SO \bot \left( {ABCD} \right)\) suy ra \(AO\) là hình chiếu của \(AS\) trên mặt phẳng \(\left( {ABCD} \right)\) \( \Rightarrow \left( {\widehat {SA\,,\,\left( {ABCD} \right)}} \right) = \left( {\widehat {SA\,;\,AO}} \right) = \widehat {SAO}\).

\(ABCD\) là hình vuông cạnh bằng \(a\) suy ra \(AO = \frac{1}{2}AC = \frac{{a\sqrt 2 }}{2}\).

Trong tam giác vuông \(SOA:\) \(\cos \widehat {SAO} = \frac{{AO}}{{SA}} = \frac{1}{2}\) \( \Rightarrow \widehat {SAO} = {60^ \circ }\).

Vậy góc giữa đường thẳng \(SA\) và mặt phẳng đáy bằng \({60^ \circ }\).

=========== Đây là các câu ÔN THI TN THPT MÔN TOÁN 2023 – CHUYÊN ĐỀ Trắc nghiệm Khoảng cách và góc trong không gian.