Một cái cột có hình dạng như hình bên (gồm 1 khối nón và một khối trụ ghép lại). Chiều cao đo được ghi trên hình, chu vi đáy là \(20\;{\rm{cm}}\). Thể tích của cột bằng A. \(\frac{{52000}}{{3\pi }}\left( {{\rm{c}}{{\rm{m}}^3}} \right)\). B. \(\frac{{5000}}{{3\pi }}\left( {{\rm{c}}{{\rm{m}}^3}} \right)\). C. \(\frac{{5000}}{\pi }\left( {{\rm{c}}{{\rm{m}}^3}} … [Đọc thêm...] vềMột cái cột có hình dạng như hình bên (gồm 1 khối nón và một khối trụ ghép lại). Chiều cao đo được ghi trên hình, chu vi đáy là \(20\;{\rm{cm}}\). Thể tích của cột bằng

[Mức độ 3] Trong không gian, khi quay một hình vuông xung quanh cạnh của nó thì được một hình trụ có diện tích xung quanh bằng diện tích của hình tròn có đường kính là \(a\sqrt 2 \). Tính thể tích \(V\)của khối trụ tròn xoay được giới hạn bởi hình trụ nói trên. A. \(V = \frac{{{a^3}}}{{12}}\). B. \(V = \pi {a^3}\). C. \(V = \frac{{\pi {a^3}}}{{24}}\). D. \(V = … [Đọc thêm...] về[Mức độ 3] Trong không gian, khi quay một hình vuông xung quanh cạnh của nó thì được một hình trụ có diện tích xung quanh bằng diện tích của hình tròn có đường kính là \(a\sqrt 2 \). Tính thể tích \(V\)của khối trụ tròn xoay được giới hạn bởi hình trụ nói trên.

Một hộp đựng bóng tennis có dạng hình trụ. Biết rằng hộp chứa vừa khít ba quả bóng tennis được xếp theo chiều dọc, các quả bóng tennis có kích thước như nhau. Thể tích phần không gian còn trống chiếm tỉ lệ \(a\% \) so với hộp đựng bóng tennis. Số \(a\)gần đúng với số nào sau đây? A. \(50\). B. \(66\). C. \(30\). D. \(33\). Lời giải: FB: công tuấn … [Đọc thêm...] vềMột hộp đựng bóng tennis có dạng hình trụ. Biết rằng hộp chứa vừa khít ba quả bóng tennis được xếp theo chiều dọc, các quả bóng tennis có kích thước như nhau. Thể tích phần không gian còn trống chiếm tỉ lệ \(a\% \) so với hộp đựng bóng tennis. Số \(a\)gần đúng với số nào sau đây?

Người ta làm tạ tập cơ tay như hình vẽ với hai đầu là hai khối trụ bằng nhau và tay cầm cũng là khối trụ. Biết hai đầu là hai khối trụ đường kính đáy bằng \(12\), chiều cao bằng \(6\), chiều dài tạ bằng \(30\) và bán kính tay cầm là \(2\). Thể tích vật liệu làm nên tạ tay đó bằng A. \(108\pi \). B. \(504\pi \). C. \(6480\pi \). D. \(502\pi \). Lời giải: Gọi … [Đọc thêm...] vềNgười ta làm tạ tập cơ tay như hình vẽ với hai đầu là hai khối trụ bằng nhau và tay cầm cũng là khối trụ. Biết hai đầu là hai khối trụ đường kính đáy bằng \(12\), chiều cao bằng \(6\), chiều dài tạ bằng \(30\) và bán kính tay cầm là \(2\). Thể tích vật liệu làm nên tạ tay đó bằng

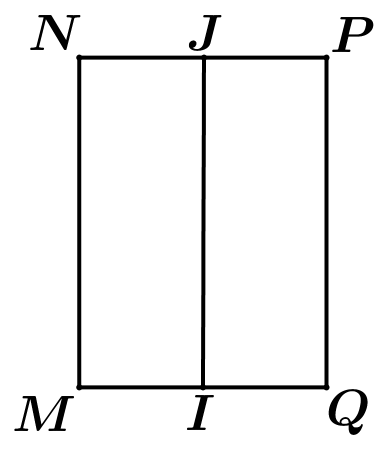
Cho hình chữ nhật \(MNPQ\) có \(MN = 8\) và chu vi của hình chữ nhật \(MNPQ\) bằng \(24\) . Gọi \(I,\;J\) lần lượt là trung điểm của \(MQ\) và \(NP\). Quay hình chữ nhật xung quanh cạnh \(IJ\) ta được một hình trụ. Tính diện tích toàn phần của hình trụ. A. \({S_{tp}} = 48\pi \). B. \({S_{tp}} = 40\pi \). C. \({S_{tp}} = 32\pi \). D. \({S_{tp}} = 96\pi \). Lời … [Đọc thêm...] vềCho hình chữ nhật \(MNPQ\) có \(MN = 8\) và chu vi của hình chữ nhật \(MNPQ\) bằng \(24\) . Gọi \(I,\;J\) lần lượt là trung điểm của \(MQ\) và \(NP\). Quay hình chữ nhật xung quanh cạnh \(IJ\) ta được một hình trụ. Tính diện tích toàn phần của hình trụ.

Cho hình thang cân \(ABCD\) có đáy là \(AB,\,\,CD\). Gọi \(M,N\) lần lượt là trung điểm của \(AB,\,\,CD\). Biết \(AB = 2a,\,\,CD = 6a,\,\,AD = 3a\), tính diện tích toàn phần của hình tròn xoay tạo thành khi cho hình thang \(ABCD\) quay quanh đường thẳng \(MN\). A. \(22\pi {a^2}\). B. \(20\pi {a^2}\). C. \(24\pi {a^2}\). D. \(36\pi {a^2}\). Lời giải: Hình … [Đọc thêm...] vềCho hình thang cân \(ABCD\) có đáy là \(AB,\,\,CD\). Gọi \(M,N\) lần lượt là trung điểm của \(AB,\,\,CD\). Biết \(AB = 2a,\,\,CD = 6a,\,\,AD = 3a\), tính diện tích toàn phần của hình tròn xoay tạo thành khi cho hình thang \(ABCD\) quay quanh đường thẳng \(MN\).

Cho hình chữ nhật \(ABCD\) có \(AC = 50\sqrt 5 \;cm\) và \(\sin \widehat {BAC} = \frac{{\sqrt 5 }}{5}\). Quay hình chữ nhật xung quanh cạnh \(BC\) ta được một hình trụ. Tính diện tích xung quanh của hình trụ. A. \(10000\pi \;c{m^2}\). B. \(2500\pi \;c{m^2}\). C. \(5000\pi \;c{m^2}\). D. \(10000\;c{m^2}\). Lời giải: Xét tam giác vuông \(ABC\) vuông tại \(B\), … [Đọc thêm...] vềCho hình chữ nhật \(ABCD\) có \(AC = 50\sqrt 5 \;cm\) và \(\sin \widehat {BAC} = \frac{{\sqrt 5 }}{5}\). Quay hình chữ nhật xung quanh cạnh \(BC\) ta được một hình trụ. Tính diện tích xung quanh của hình trụ.

Quay một hình vuông cạnh \(10\)cm quanh đường thẳng đi qua trung điểm hai cạnh đối của nó ta được một hình trụ. Diện tích xung quanh của hình trụ thu được là A. \(100\pi \;c{m^2}\). B. \(200\pi \;c{m^2}\). C. \(250\pi \;c{m^2}\). D. \(500\pi \;c{m^2}\). Lời giải: Do hình trụ có chiều cao bằng \(h = 10\)nên đường sinh \(l = 10\). Hình trụ có bán kính \(r = … [Đọc thêm...] vềQuay một hình vuông cạnh \(10\)cm quanh đường thẳng đi qua trung điểm hai cạnh đối của nó ta được một hình trụ. Diện tích xung quanh của hình trụ thu được là

Người ta cắt hai hình cầu có bán kính lần lượt là \(R = 13cm\) và \(r = \sqrt {41} \,cm\) để làm hồ lô đựng rượu như hình vẽ sau. Biết đường tròn giao của hai hình cầu có bán kính \(r' = 5cm\) và nút uống rượu là một hình trụ có bán kính đáy bằng \(\sqrt 5 cm\), chiều cao bằng \(4cm\). Giả sử độ dày vỏ hồ lô không đáng kể. Hỏi hồ lô đựng được bao nhiêu lít rượu? (Kết … [Đọc thêm...] vềNgười ta cắt hai hình cầu có bán kính lần lượt là \(R = 13cm\) và \(r = \sqrt {41} \,cm\) để làm hồ lô đựng rượu như hình vẽ sau.

Biết đường tròn giao của hai hình cầu có bán kính \(r’ = 5cm\) và nút uống rượu là một hình trụ có bán kính đáy bằng \(\sqrt 5 cm\), chiều cao bằng \(4cm\). Giả sử độ dày vỏ hồ lô không đáng kể. Hỏi hồ lô đựng được bao nhiêu lít rượu? (Kết quả làm tròn đến hàng phần chục).