Giải bài 9.19 trang 58 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
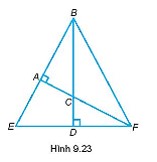
Cho tam giác ABC vuông. Kẻ đường thẳng vuông góc với cạnh huyền BC của tam giác ABC tại điểm D không thuộc đoạn BC. Nó cắt đường thẳng chứa cạnh AB tại E và cắt đường thẳng chứa cạnh AC tại F. Xác định trực tâm của tam giác BEF.
Phương pháp giải:
Trong một tam giác, giao điểm của 2 đường cao là trực tâm của tam giác đó.
Lời giải chi tiết:

Xét tam giác BEF, có:
\(BC \bot EF\)
=> Đường cao xuất phát từ B là đường thẳng BD
\(FA \bot BA\)
=> Đường cao xuất phát từ F là đường thẳng FA
Mà FA cắt BD tại C
=> C là trực tam giác ABC.
–>
— *****
Giải bài 9.20 trang 58 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
Cho P là một điểm nằm trong góc nhọn xOy. Gọi M là điểm sao cho Ox là đường trung trực của đoạn thẳng PM, gọi N là điểm sao cho Oy là đường trung trực của đoạn thẳng PN. Đường thẳng MN cắt Ox tại R, cắt Oy tại S.Chứng minh tia PO là tia phân giác của góc RPS.
Phương pháp giải:
-O, R cùng nằm trên đường trung trực PM, chứng minh \(\widehat {OPR} = \widehat {OMR}\).
-O,S cùng nằm trên đường trung trực PN, chứng minh \(\widehat {OPS} = \widehat {ONS}\).
Lời giải chi tiết:
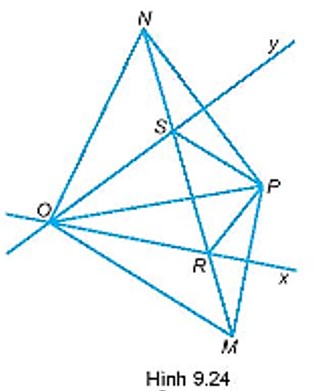
Ta có: O, R nằm trên đường trung trực của PM
\( \Rightarrow OP = OM;RP = RM\) (1)
\( \Rightarrow \)Tam giác OPM cân tại O, tam giác RPM cân tại R.
\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}\widehat {OPM} = \widehat {OMP}\\\widehat {RPM} = \widehat {RMP}\end{array} \right.\\ \Rightarrow \widehat {OPR} = \widehat {OMR}\end{array}\)
Tương tự: O, S nằm trên đường trung trực của PN
\( \Rightarrow OP = ON;SP = SN\)(2)
\( \Rightarrow \)Tam giác OPN cân tại O, tam giác SPN cân tại S.
\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}\widehat {OPN} = \widehat {ONP}\\\widehat {SPN} = \widehat {SNP}\end{array} \right.\\ \Rightarrow \widehat {OPS} = \widehat {ONS}\end{array}\)
Từ (1) và (2) suy ra: OM = ON = OP hay OM = ON
\( \Rightarrow \)Tam giác OMN cân tại O
\( \Rightarrow \widehat {OMN} = \widehat {ONM}\)
Hay \(\widehat {OMR} = \widehat {ONS}\)
\( \Rightarrow \widehat {OPR} = \widehat {OPS}\)
Vậy tia PO là tia phân giác của góc RPS.
–>
— *****
Giải bài 9.21 trang 58 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
Gọi H là trực tâm của tam giác nhọn ABC. Khi AH = BC, hãy chứng minh \(\widehat {BAC} = {45^0}\).
Phương pháp giải:
-Kẻ đường cao BJ của tam giác ABC.
-Chứng minh: \(\Delta AHJ = \Delta BCJ\left( {ch – gn} \right)\)
-Chứng minh tam giác ABJ vuông cân tại J.
Lời giải chi tiết:
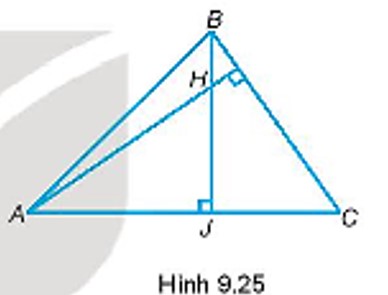
Gọi BJ là đường cao xuất phát từ B của tam giác ABC
\( \Rightarrow BJ \bot AC\)
Xét \(\Delta AHJ\) và \(\Delta BCJ\) có:
\(\begin{array}{l}\widehat {AJH} = \widehat {BJC} = {90^0}\\\left\{ \begin{array}{l}\widehat {JAH} + \widehat {JCB} = {90^0}\\\widehat {JBC} + \widehat {JCB} = {90^0}\end{array} \right. \Rightarrow \widehat {JAH} = \widehat {JBC}\\AH = BC\left( {gt} \right)\\ \Rightarrow \Delta AHJ = \Delta BCJ\left( {ch – gn} \right)\end{array}\)
\( \Rightarrow AJ = BJ\)(cạnh tương ứng)
Mà tam giác JAB vuông tại J nên JAB là tam giác vuông cân.
Vậy \(\widehat {BAC} = {45^0}\)
–>
— *****
Giải bài 9.22 trang 58 SBT Toán 7 Kết nối tri thức tập 2 – KNTT
a) Giả sử đường trung trực d của cạnh BC của tam giác ABC cắt cạnh AC tại một điểm D nằm giữa A và C. Chứng minh AC > AB.
b) Hỏi đảo lại có đúng không tức là nếu tam giác ABC có AC > AB thì đường trung trực d của cạnh BC có cắt AC tại điểm nằm giữa A và C không?
c) Vẫn giả sử đường trung trực d của cạnh BC của tam giác ABC cắt cạnh AC tại một điển D nằm giữa A và C. Với M là một điểm tuỳ ý thuộc d, M khác D, hãy chứng minh MA + MB > DA + DB.
Phương pháp giải:
-Điểm nằm trên đường trung trực của đoạn thẳng thì cách đều 2 đầu mút của đoạn thẳng đó.
-Đường trung trực của cạnh BC cắt AC tại M, M nằm giữa A và C thì: MB = MC
Lời giải chi tiết:
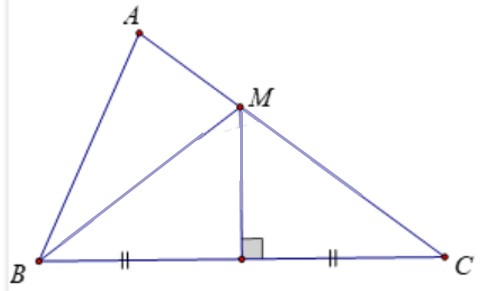
a)
Đường trung trực của cạnh BC cắt AC tại M, M nằm giữa A và C thì: MB = MC
=>AC = AM + MC = AM + MB
Áp dụng bất đẳng thức cho tam giác cho tam giác ABM có:
AM + MB > AB
=>AC > AB.
b)
Điều đảo lại cũng đúng: đường trung trực của BC không thể đi qua A vì nếu thế thì AC = AB,
=>d phải cắt đoạn thẳng AB tại điểm nằm giữa A và B, khi đó AB > AC (cm tương tự câu a) hoặc phải cắt đoạn thẳng AC tại điểm nằm giữa A và C, lúc đó AC > AB
Mà gt AC > AB nên đường trung trực của đoạn thẳng BC phải cắt đoạn thẳng AC tại điểm nằm giữa A và C.
c)
Do MB = MC nên MA + MB = MA + MC
Vì M khác D, trong tam giác AMC theo bất đẳng thức tam giác, ta có:
MA + MC > AC = AD + DC = AD + DB.
–>
— *****
