Ví dụ Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Dạng 1: Tìm GTLN và GTNN của hàm số trên miền D

Ví dụ :  

Tìm GTLN-GTNN của các hàm số sau:

a) Hàm số \(y=x^3-3x^2-9x+5\).

b) Hàm số \(y=\frac{x^2+2x+3}{x-1},x\in(1;3].\)

c. $y = \frac{{x + \sqrt {1 + 9{x^2}} }}{{8{x^2} + 1}}$ trên khoảng $\left( {0; + \infty } \right).$

Lời giải:

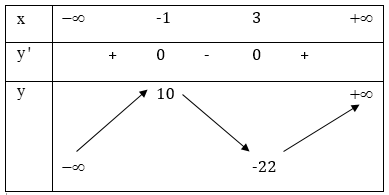
a) Hàm số \(y=x^3-3x^2-9x+5\).

• TXĐ: \(D=\mathbb{R}.\)
• \(y’=3x^2-6x-9.\)
• \(y’ = 0 \Leftrightarrow 3{x^2} – 6x – 9 = 0 \Leftrightarrow \left[ \begin{array}{l} x = – 1\\ x = 3 \end{array} \right.\)
• Bảng biến thiên:

Vậy hàm số không có Maxy; Miny.

b)  Xét hàm số \(y=\frac{x^2+2x+3}{x-1}\) xác định trên \((1;3].\)

• ​\(y’=\frac{x^2-2x-5}{(x+1)^2}\)
• \(y’ = 0 \Rightarrow {x^2} – 2x – 5 = 0 \Leftrightarrow \left[ \begin{array}{l} x = 1 + \sqrt 6 \notin \left( {1;3} \right]\\ x = 1 – \sqrt 6 \notin \left( {1;3} \right] \end{array} \right.\)
• Bảng biến thiên:

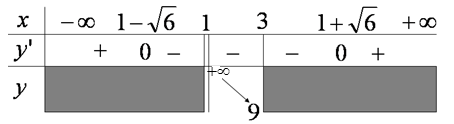
• Vậy hàm số có giá trị nhỏ nhất \(\mathop {Min}\limits_{x \in (1;3]} y = 9\), Hàm số không có giá trị lớn nhất.

c. Hàm số đã cho xác định và liên tục trên khoảng $\left( {0; + \infty } \right).$
$y = \frac{{x + \sqrt {9{x^2} + 1} }}{{8{x^2} + 1}}$ $ = \frac{{9{x^2} + 1 – {x^2}}}{{\left( {8{x^2} + 1} \right)\left( {\sqrt {9{x^2} + 1} – x} \right)}}$ $ = \frac{1}{{\sqrt {9{x^2} + 1} – x}}.$
Hàm số đạt giá trị lớn nhất trên khoảng $\left( {0; + \infty } \right)$ khi hàm số $f\left( x \right) = \sqrt {9{x^2} + 1} – x{\rm{ }}$ đạt giá trị nhỏ nhất trên khoảng $\left( {0; + \infty } \right).$
Ta có: $f’\left( x \right) = \frac{{9x}}{{\sqrt {9{x^2} + 1} }} – 1$ với mọi $x \in \left( {0; + \infty } \right).$
Ta tìm nghiệm của phương trình $f’\left( x \right)$ trên khoảng $\left( {0; + \infty } \right).$
$f’\left( x \right) = 0,x \in \left( {0; + \infty } \right)$ $ \Leftrightarrow \left\{ \begin{array}{l}
x > 0\\
\sqrt {9{x^2} + 1} = 9x
\end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l}
x > 0\\
72{x^2} = 1
\end{array} \right. \Leftrightarrow x = \frac{1}{{6\sqrt 2 }}.$
$\mathop {\min }\limits_{x > 0} f\left( x \right) = \frac{{{\rm{2}}\sqrt {\rm{2}} }}{{\rm{3}}}$ khi $x = \frac{{\rm{1}}}{{{\rm{6}}\sqrt {\rm{2}} }}$ $ \Rightarrow \mathop {{\rm{max}}y}\limits_{x > {\rm{0}}} = \frac{1}{{\frac{{{\rm{2}}\sqrt {\rm{2}} }}{{\rm{3}}}}} = \frac{{3\sqrt 2 }}{4}$ khi $x = \frac{{\rm{1}}}{{{\rm{6}}\sqrt {\rm{2}} }}.$
Hàm số không có giá trị nhỏ nhất khi $x > 0.$

Dạng 2: Tìm GTLN và GTNN của hàm số trên một đoạn

Ví dụ:

Tìm GTLN-GTNN của các hàm số sau:

a) Hàm số \(y = f\left( x \right) = – \frac{1}{3}{x^3} + {x^2} – 2x + 1\) trên đoạn \(\left[ { – 1;0} \right]\).

b) Hàm số \(y = f\left( x \right) = \frac{{2x + 1}}{{x – 2}}\) trên đoạn \(\left[ { – \frac{1}{2};1} \right]\).

c) Hàm số \(y = f\left( x \right) = {\sin ^2}x – 2\cos x + 2\).

Lời giải:

a) Hàm số \(y = f\left( x \right) = – \frac{1}{3}{x^3} + {x^2} – 2x + 1\) xác định trên đoạn \(\left[ { – 1;0} \right]\).

• \({f^/}\left( x \right) = – {x^2} + 2x – 2\)
• \({f^/}\left( x \right) = 0 \Leftrightarrow – {x^2} + 2x – 2 = 0\)
• Ta có: \(f\left( { – 1} \right) = \frac{{11}}{3};f\left( 0 \right) = 1\).
• Vậy: \(\mathop {\max f\left( x \right)}\limits_{\left[ { – 1;0} \right]} = \frac{{11}}{3}\); \(\mathop {\min f\left( x \right)}\limits_{\left[ { – 1;0} \right]} = 1\)

b) Hàm số \(y = f\left( x \right) = \frac{{2x + 1}}{{x – 2}}\) xác định trên đoạn \(\left[ { – \frac{1}{2};1} \right]\)

• \({f^/}\left( x \right) = – \frac{5}{{{{\left( {x – 2} \right)}^2}}} < 0,\forall x \in\left [ -\frac{1}{2};1 \right ]\)
• Ta có: \(f\left( { – \frac{1}{2}} \right) = 0;f\left( 1 \right) = – 3\)
• Vậy: \(\mathop {\max f\left( x \right)}\limits_{\left[ { – \frac{1}{2};1} \right]} = 0\); \(\mathop {min f\left( x \right)}\limits_{\left[ { – \frac{1}{2};1} \right]} = – 3\)

c)  Hàm số \(y = f\left( x \right) = {\sin ^2}x – 2\cos x + 2\).

• TXĐ: \(D=\mathbb{R}\)
• Ta có: \(f\left( x \right) = {\sin ^2}x – 2\cos x + 2 = – c{\rm{o}}{{\rm{s}}^2}x – 2co{\mathop{\rm s}\nolimits} x + 3\)
• Đặt: \(t = {\cos ^2}x\) suy ra \(t \in \left[ { – 1;1} \right];\forall x \in \mathbb{R}\).
• Xét hàm số: \(g\left( t \right) = – {t^2} – 2t + 3\) trên đoạn \([-1;1]\).
  • Ta có: \({g^/}\left( t \right) = – 2t – 2\)
  •   \({g^/}\left( t \right) = 0 \Leftrightarrow t = – 1\)
  • Tính: \(g\left( { – 1} \right) = 4;g\left( 1 \right) = 0\).
• Vậy: \(\max f(x) = \mathop {\max }\limits_{{\rm{[}} – 1;1]} g(t) = 4\); \(\min f(x) = \mathop {\min }\limits_{{\rm{[}} – 1;1]} g(t) = 0\).

Dạng khác – Thực tế

Ví dụ 1 . Tìm GTLN và GTNN của các hàm số sau:
a. $y = (x + 3)\sqrt { – {x^2} – 2x + 3} .$
b. $y = \sqrt {45 + 20{x^2}} + \left| {2x – 3} \right|.$

a. Hàm số xác định $ \Leftrightarrow – {x^2} – 2x + 3 \ge 0$ $ \Leftrightarrow – 3 \le x \le 1.$
Vậy hàm số xác định trên $D = [ – 3;1].$
$y’ = \frac{{ – 2{x^2} – 6x}}{{\sqrt { – {x^2} – 2x + 3} }}$ $ \Rightarrow y’ = 0$ $ \Leftrightarrow \left\{ \begin{array}{l}
x \in ( – 3;1)\\
– 2{x^2} – 6x = 0
\end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l}
x \in ( – 3;1)\\
x = 0,x = – 3
\end{array} \right.$ $ \Leftrightarrow x = 0.$
${\rm{y}}\left( { – {\rm{ 3}}} \right) = 0$, ${\rm{y}}\left( {\rm{1}} \right) = 0$, ${\rm{y}}\left( 0 \right) = 3\sqrt 3 .$
$f$ liên tục trên $[ – 3;1]$ và có đạo hàm trên $( – 3;1).$
Suy ra $\mathop {\max }\limits_{x \in D} y = 3\sqrt 3 $ khi $x = 0$, $\mathop {\min }\limits_{x \in D} y = 0$ khi $x = – 3$ hoặc $x = 1.$
b. Áp dụng bất đẳng thức B.C.S (Bunyakovsky), ta có:
$\sqrt {45 + 20{x^2}} = \sqrt {5(9 + 4{x^2})} $ $ = \sqrt {({2^2} + {1^2})[{3^2} + {{(2x)}^2}]}$ $\mathop \ge \limits^{BCS} $ $\left| {2.3 + 1.2x} \right| = \left| {6 + 2x} \right|.$
Suy ra $y \ge \left| {6 + 2x} \right| + \left| {2x – 3} \right|.$
Áp dụng bất đẳng thức $\left| a \right| + \left| b \right| \ge \left| {a + b} \right|$, ta có:
$\left| {6 + 2x} \right| + \left| {2x – 3} \right|$ $ = \left| {6 + 2x} \right| + \left| {3 – 2x} \right|$ $ \ge \left| {6 + 2x + 3 – 2x} \right| = 9.$
Suy ra $y \ge 9.$
$y = 9$ $ \Leftrightarrow \left\{ \begin{array}{l}
(6 + 2x)(3 – 2x) \ge 0\\
\frac{{2x}}{1} = \frac{3}{2}
\end{array} \right.$ $ \Leftrightarrow x = \frac{3}{4}.$
Vậy ${\rm{miny}} = {\rm{9}}$ khi $x = \frac{3}{4}.$

Ví dụ 2 .  Cho hai số thực $x, y$ thoả mãn: $\left\{ \begin{array}{l}
x \ge 0,{\rm{ }}y \ge 1\\
x + y = 3
\end{array} \right.$. Tìm giá trị nhỏ nhất, giá trị lớn nhất của biểu thức: $P = {x^3} + 2{y^2} + 3{x^2} + 4xy – 5x.$

Ta có $y = 3 – x \ge 1$ $ \Rightarrow x \le 2 \Rightarrow x \in \left[ {0;2} \right].$
Khi đó: $P = {x^3} + 2{(3 – x)^2} + 3{x^2} + 4x(3 – x) – 5x$ $ = {x^3} + {x^2} – 5x + 18.$
Xét hàm số $f(x) = {x^3} + {x^2} – 5x + 18$ trên $\left[ {0;2} \right]$, ta có:
$f'(x) = 3{x^2} + 2x – 5$ $ \Rightarrow f'(x) = 0 \Leftrightarrow x = 1.$
Hơn nữa: $f\left( 0 \right) = 18,$, $f\left( 1 \right) = 15$, $f\left( 2 \right) = 20.$
Vậy: $\max P = \mathop {\max }\limits_{{\rm{x}} \in {\rm{[}}0;2]} f(x) = f(2) = 20$ khi $x = 2$, $\min P = \mathop {\min }\limits_{{\rm{x}} \in {\rm{[}}0;2]} f(x) = f(1) = 15$ khi $x = 1.$

Ví dụ 3 . Cho hai số thực $a,b \ge 0$. Chứng minh: ${a^4} + {b^4} \ge {a^3}b + {b^3}a$ $(1).$

+ Nếu một trong hai số $a, b$ bằng $0$ thì $(1)$ luôn đúng.
+ Với $a \ne 0$, đặt $b = ta$. Khi đó $(1)$ trở thành:
${a^4}(1 + {t^4}) \ge {a^4}(t + {t^3})$ $ \Leftrightarrow {t^4} – {t^3} – t + 1 \ge 0.$
Xét hàm số $f(t) = {t^4} – {t^3} – t + 1$, ta có: $f'(t) = 4{t^3} – 3{t^2} – 1$ $ = (t – 1)(4{t^2} + t + 1).$
$ \Rightarrow f'(t) = 0 \Leftrightarrow t = 1.$
Lập bảng biến thiên, từ đó suy ra $f(t) \ge f(0) = 0$. Từ đó suy ra ${a^4} + {b^4} \ge {a^3}b + {b^3}a$ với $a,b \ge 0$.

Ví dụ 4 . Cho các số thực dương $x, y$. Tìm giá trị lớn nhất của biểu thức: $P = \frac{{4x{y^2}}}{{{{\left( {x + \sqrt {{x^2} + 4{y^2}} } \right)}^3}}}.$

Đặt $x = ty$ ta có $P = \frac{{4t}}{{{{\left( {t + \sqrt {{t^2} + 4} } \right)}^3}}}.$
Xét $f\left( t \right) = \frac{{4t}}{{{{\left( {t + \sqrt {{t^2} + 4} } \right)}^3}}}$, $t > 0.$
Ta có: $f’\left( t \right) = \frac{{4\left( {\sqrt {{t^2} + 4} – 3t} \right)}}{{\sqrt {{t^2} + 4} {{\left( {t + \sqrt {{t^2} + 4} } \right)}^3}}}$ và $f’\left( t \right) = 0 \Leftrightarrow \sqrt {{t^2} + 4} = 3t$ $ \Leftrightarrow t = \frac{1}{{\sqrt 2 }}.$
Lập bảng biến thiên ta được $\mathop {\max }\limits_{(0; + \infty )} f\left( t \right) = f\left( {\frac{1}{{\sqrt 2 }}} \right) = \frac{1}{8}.$
Vậy $\max P = \frac{1}{8}$ khi $x = \frac{1}{{\sqrt 2 }}y.$

Ví dụ 5 . Tìm tất cả các giá trị của $a$ và $b$ thoả mãn điều kiện: $a \ge – \frac{1}{2}$ và $\frac{a}{b} > 1$ sao cho biểu thức $P = \frac{{2{a^3} + 1}}{{b\left( {a – b} \right)}}$ đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó.

Từ giả thiết, ta suy ra $a \ne 0$ và $b(a – b) > 0.$
Ta có: $0 < b(a – b) \le \frac{{{a^2}}}{4}$ và $2{a^3} + 1 > 0$ nên $P \ge \frac{{2{a^3} + 1}}{{{a^2}}} = f(a).$
Xét hàm số $f(a),{\rm{ }}a \ge – \frac{1}{2}$ có $f'(a) = \frac{{2{a^3} – 2}}{{{a^3}}}$ $ \Rightarrow f(a) = 0 \Leftrightarrow a = 1.$
Bảng biến thiên:

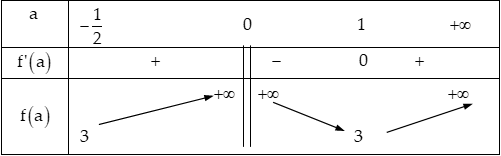
Từ bảng biến thiên $ \Rightarrow f(a) \ge 3{\rm{ }}, \forall a \ge – \frac{1}{2}$ $ \Rightarrow P \ge – \frac{1}{2}.$
Đẳng thức xảy ra $ \Leftrightarrow \left\{ \begin{array}{l}
a = – \frac{1}{2}\\
b = – \frac{1}{4}
\end{array} \right.$ hoặc $\left\{ \begin{array}{l}
a = 1\\
b = \frac{1}{2}
\end{array} \right.$
Vậy $\min P = 3$ khi $\left( {a;b} \right) = \left( { – \frac{1}{2}; – \frac{1}{4}} \right),\left( {1;\frac{1}{2}} \right)$.

Ví dụ 6 . Tìm GTLN và GTNN của hàm số sau: $y = \frac{{\sqrt {x + 1} + 2\sqrt {3 – x} + 2}}{{2\sqrt {x + 1} + \sqrt {3 – x} + 1}}$ trên $\left[ { – 1;3} \right].$

Vì ${\left( {\sqrt {x + 1} } \right)^2} + {\left( {\sqrt {3 – x} } \right)^2} = 4$, suy ra tồn tại số thực $t \in \left[ {0;1} \right]$ sao cho $\sqrt {x + 1} = \frac{{4t}}{{1 + {t^2}}}$, $\sqrt {3 – x} = \frac{{2(1 – {t^2})}}{{1 + {t^2}}}.$
Khi đó: $y = \frac{{2{t^2} – 4t – 6}}{{{t^2} – 8t – 3}} = f(t)$, xét $f(t) = \frac{{2{t^2} – 4t – 6}}{{{t^2} – 8t – 3}}$ với $t \in \left[ {0;1} \right].$
Ta có: $f'(t) = \frac{{ – 12{t^2} – 36}}{{{{({t^2} – 8t – 3)}^2}}} < 0$ $\forall t \in \left[ {0;1} \right]$ nên $f(t)$ nghịch biến trên đoạn $\left[ {0;1} \right].$
Hơn nữa: $f(0) = 2$, $f(1) = \frac{4}{5}.$
Vậy $\min y = \mathop {\min }\limits_{t \in \left[ {0;1} \right]} f(t) = f(0) = 2$ khi $x = 0$, $\max y = \mathop {\max }\limits_{t \in \left[ {0;1} \right]} f(t) = f(1) = \frac{4}{5}$ khi $x = 1.$