Trả lời câu hỏi trong bài 22 Ba đường conic – Kết nối

Trả lời câu hỏi trong bài 22 Ba đường conic
=============

1. ELIP

Hoạt động 1:  Đính hai đầu của một sợi dây không đàn hồi vào hai vị trí cố định F₁, F₂ tren một mặt bàn (độ dài sợi dây lớn hơn khoảng cách giữa hai điểm F₁, F₂ ). Kéo căng sợi dây tại một điểm M bởi một đầu bút dạ (hoặc phấn). Di chuyển đầu bút dạ để nó vẽ trên mặt bàn một đường khép kín.

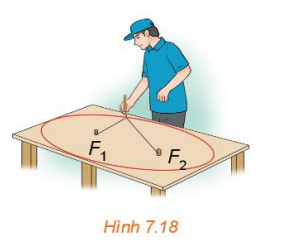
a. Đường vừa nhận được có liên hệ với hình ảnh nào ở Hình 7.17?

b. Trong quá trinh đầu bút di chuyển để vẽ nên đường nói trên, tổng các khoảng cách từ nó tới các vị trí F₁, F₂ có thay đổi không? Vì sao?

Hướng dẫn giải:

a. Đường nhận được liên hệ với hình b.

 

b. Tổng các khoảng cách từ đầu bút tới các vị trí F₁, F₂ không thay đổi vì nó luôn bằng độ dài dây 

Câu hỏi:  Tại sao trong định nghĩa elip cần điều kiện a > c?

Hướng dẫn giải:

Xét tam giác MF₁F₂ có: MF₁+ MF₂ = 2a > F₁F₂ =2c (bất đẳng thức tam giác). Suy ra: a > c.

Luyện tập 1: Trên bàn bida hình elip có một lỗ thu bi tại một tiêu điểm. Nếu gậy chơi tác động đủ mạnh vào một bi đặt tại tiêu điểm còn lại của bàn, thì sau khi va vào thành bàn, bi sẽ bật lại và chạy về lỗ thu (bỏ qua các tác động phụ). Hỏi độ dài quãng đường bi lăn từ điểm xuất phát tới lỗ thu có phụ thuộc vào đường đi của bi hay không? Vì sao?

Hướng dẫn giải:

Ta có vị trí ban đầu của bi và vị trí của lỗ thu là 2 tiêu điểm của hình elip, gọi lần lượt là F₁ và F₂. Bi lăn từ F₁ đến một vị trí M trên hình elip rồi đi đến F₂. Vậy quãng đường bi đi được là: MF₁+ MF₂ 

Theo tính chất hình elip thì MF₁+ MF₂ = 2a, không đổi

Suy ra độ dài quãng đường bi lăn từ điểm xuất phát tới lỗ thu không phụ thuộc vào đường đi của bi.

Hoạt động 2:  Xét một elip (E) với các kí hiệu như trong định nghĩa. Chọn hệ trục tọa độ Oxy có gốc O là trung điểm của F₁F₂ , tia Ox trùng tia OF₂ 

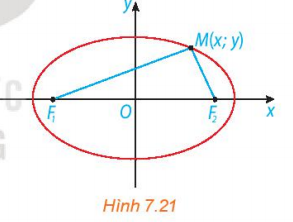
a. Nêu tọa độ của các tiêu điểm F₁, F₂

b. Giải thích vì sao điểm M(x; y) thuộc elip khi và chỉ khi: $\sqrt{(x+c)^{2}+y^{2}}+\sqrt{(x-c)^{2}+y^{2}}=2a$

Hướng dẫn giải:

a. Vì F₁F₂ = 2c, mà O là trung điểm của F₁, F₂

Tọa độ của các điểm: F₁(-c; 0) và F₂(c; 0) 

b.

• Giả sử M thuộc elip (E) ta chứng minh: $\sqrt{(x+c)^{2}+y^{2}}+\sqrt{(x-c)^{2}+y^{2}}=2a$. Thật vậy:

M thuộc elip (E) nên: MF₁+ MF₂ = 2a 

$\Rightarrow$ $\sqrt{(x+c)^{2}+y^{2}}+\sqrt{(x-c)^{2}+y^{2}}=2a$.

• Giả sử $\sqrt{(x+c)^{2}+y^{2}}+\sqrt{(x-c)^{2}+y^{2}}=2a$, ta chứng minh  M thuộc elip (E). Thật vậy:

$\sqrt{(x+c)^{2}+y^{2}}+\sqrt{(x-c)^{2}+y^{2}}=2a$ nên: MF₁+ MF₂ = 2a 

$\Rightarrow$ M thuộc elip (E).

Luyện tập 2: Cho elip có phương trình chính tắc $\frac{x^{2}}{100}+\frac{y^{2}}{64}=1$. Tìm các tiêu điểm và tiêu cự của elip.

Hướng dẫn giải:

Có: a² = 100, b² = 64 => c = $\sqrt{a^{2}-b^{2}}$ = 6. Vậy elip có hai tiêu điểm là F₁(-6; 0) và F₂(6; 0) và tiệu cự là F₁F₂ = 2c = 12.

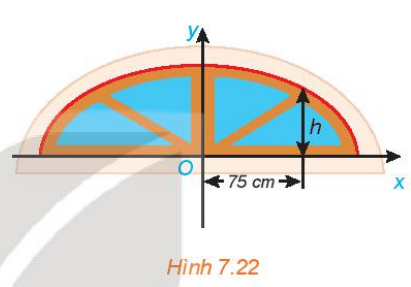
Vận dụng 1:  Trong bản vẽ thiết kế, vòm của ô thoáng trong Hình 7.22 là nửa nằm phía trên trục hoành của elip có phương trình

$\frac{x^{2}}{16}+\frac{y^{2}}{4}=1$.

Biết rằng 1 đơn vị trên mặt phẳng tọa độ của bản vẽ thiết kế ứng với 30 cm trên thực tế. Tính chiều cao h của ô thoáng tại điểm cách điểm chính giữa của đế ô thoáng 75 cm.

Hướng dẫn giải:

Ta có 75cm trên thực tế ứng với 2,5 đơn vị trên mặt phẳng tọa độ.

Gọi điểm M trên elip thỏa mãn có hoành độ là 2,5 => tọa độ M(2,5; y)

Mà M thuộc (E) nên: $\frac{2,5^{2}}{16}+\frac{y^{2}}{4}=1$.

$\Rightarrow$ y² = $\frac{39}{16}$ nên y $\approx $ 1,56

Vậy chiều cao của ô thoáng là: h = 1,56.30 = 46,8 cm.

2. HYPEBOL

Câu hỏi:  Tại sao trong định nghĩa hypebol cần điều kiện a < c?

Trả lời: Xét tam giác MF₁F₂ có: |MF₁ – MF₂ | = 2a < F₁F₂ =2c (bất đẳng thức tam giác). Suy ra: a < c.

Luyện tập 3:  Cho hình chữ nhật ABCD và M, N tương ứng là trung điểm của các cạnh AB, CD. Chứng minh rằng bốn điểm A, B, C, D cùng thuộc một hypebol có hai tiêu điểm là M và N.

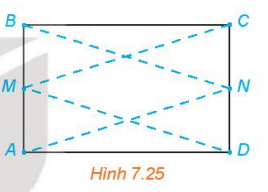
Hướng dẫn giải:

Do M, N tương ứng là trung điểm của các cạnh AB, CD và tính chất hình chữ nhật ABCD ta có: BM = CN = AM = DN và BN = CM = AN = DM.

Từ đó: |BN – BM| = |CN – CM| = |AN – AM| = |DN – DM| > MN (bất đẳng thức tam giác).

Vậy A, B, C, D cùng thuộc một hypebol có hai tiêu điểm là M và N.

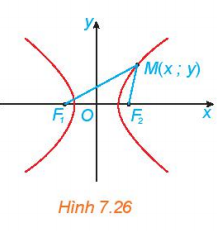
Hoạt động 3:  Xét một hypebol (H) với các kí hiệu như trong định nghĩa. Chọn hệ trục Oxy có gốc O là trung điểm của F₁F₂ . Giải thích vì sao điểm M(x; y) thuộc (H) khi và chỉ khi

$\left | \sqrt{(x+c)^{2}+y^{2}}-\sqrt{(x-c)^{2}+y^{2}}\right |=2a$

Hướng dẫn giải:

a. Vì F₁F₂ = 2c, mà O là trung điểm của F₁, F₂

Tọa độ của các điểm: F₁(-c; 0) và F₂(c; 0) 

b.

• Giả sử M thuộc hypebol (H) ta chứng minh: $\left | \sqrt{(x+c)^{2}+y^{2}}-\sqrt{(x-c)^{2}+y^{2}}\right |=2a$. Thật vậy:

M thuộc hypebol (H) nên: |MF₁ – MF₂|= 2a 

$\Rightarrow$ $\left | \sqrt{(x+c)^{2}+y^{2}}-\sqrt{(x-c)^{2}+y^{2}}\right |=2a$

• Giả sử $\left | \sqrt{(x+c)^{2}+y^{2}}-\sqrt{(x-c)^{2}+y^{2}}\right |=2a$, ta chứng minh  M thuộc hypebol (H). Thật vậy:

$\left | \sqrt{(x+c)^{2}+y^{2}}-\sqrt{(x-c)^{2}+y^{2}}\right |=2a$ nên: |MF₁ – MF2| = 2a 

$\Rightarrow$ M thuộc hypebol (H).

Luyện tập 4:  Cho (H): $\frac{x^{2}}{144}-\frac{y^{2}}{25}=1$. Tìm các tiêu điểm và tiêu cự của (H).

Hướng dẫn giải:

Có: a² = 144, b² = 25 => c = $\sqrt{a^{2}+b^{2}}$ = 13. Vậy elip có hai tiêu điểm là F₁(-13; 0) và F₂(13; 0) và tiệu cự là F₁F₂ = 2c = 26.

3. PARABOL

Hoạt động 4:  Cho parabol (P): y = $\frac{1}{4}x^{2}$. Xét F(0; 1) và đường thẳng $\Delta $: y + 1 = 0. Với điểm M(x; y) bất kì, chứng minh rằng MF = d(M, $\Delta $) $\Leftrightarrow$ M(x; y) thuộc (P).

Hướng dẫn giải:

Ta có: MF = $\sqrt{x^{2}+(y-1)^{2}}$, 

d(M, $\Delta $)= $\frac{|y+1|}{\sqrt{1^{2}+0}}=|y+1|$

• Giả sử MF = d(M, $\Delta $), ta chứng minh M(x; y) thuộc (P). Thật vậy:

MF = d(M, $\Delta $) $\Leftrightarrow$ $\sqrt{x^{2}+(y-1)^{2}}$ = $|y+1|$

$\Rightarrow$ $x^{2}+(y-1)^{2}$ = $(y+1)^{2}$

$\Leftrightarrow$ $x^{2}-4y=0\Leftrightarrow y=\frac{1}{4}x^{2}$

Vậy M thuộc (P).

• Giả sử M(x; y) thuộc (P), ta chứng minh MF = d(M, $\Delta $).

M(x; y) thuộc (P) $\Rightarrow$ y = $\frac{1}{4}x^{2}$ hay $x^{2}=4y$ thay vào biểu thức tính MF có:

MF = $\sqrt{x^{2}+(y-1)^{2}}$ = $\sqrt{4y+(y-1)^{2}}=\sqrt{y^{2}+2y+1}=\sqrt{(y+1)^{2}}=|y+1|$ = d(M, $\Delta $)

Vậy  MF = d(M, $\Delta $).

Hoạt động 5:  Xét (P) là một parabol với tiêu điểm F và đường chuẩn $\Delta $. Gọi p là tham số tiêu của (P) và H là hình chiếu vuông góc của F trên $\Delta $. Chọn hệ trục tọa độ Oxy có gốc O là trung điểm của HF, tia Ox trùng tia OF (H.7.27)

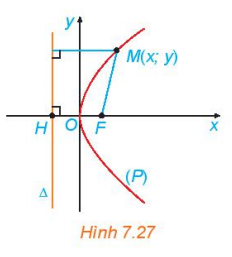
a. Nêu tọa độ của F và phương trình của $\Delta $

b. Giải thích vì sao điểm M(x; y) thuộc (P) khi và chỉ khi $\sqrt{\left ( x-\frac{p}{2} \right )^{2}+y^{2}}=\left | x+\frac{p}{2} \right |$

Hướng dẫn giải:

a. Do O là trung điểm HF, mà HF = p (tham số tiêu của (P)) nên tọa độ của F là: F$\left ( \frac{p}{2};0 \right )$.

Đường thẳng $\Delta $ đi qua H$\left ( \frac{-p}{2};0 \right )$ và vuông góc với trục Ox nên có phương trình: $x= \frac{-p}{2}$

b.

Ta có: MF = $\sqrt{\left ( x-\frac{p}{2} \right )^{2}+y^{2}}$

d(M, $\Delta $)= $\frac{\left | x+\frac{-p}{2} \right |}{\sqrt{1^{2}+0}}=\left | x+\frac{-p}{2} \right |$

• Giả sử M thuộc (P), ta chứng minh  $\sqrt{\left ( x-\frac{p}{2} \right )^{2}+y^{2}}=\left | x+\frac{p}{2} \right |$. Thật vậy:

M thuộc (P) $\Rightarrow$ MF = d(M, $\Delta $)

$\Leftrightarrow$ $\sqrt{\left ( x-\frac{p}{2} \right )^{2}+y^{2}}=\left | x+\frac{p}{2} \right |$

• Giả sử $\sqrt{\left ( x-\frac{p}{2} \right )^{2}+y^{2}}=\left | x+\frac{p}{2} \right |$, ta chứng minh M thuộc (P). Thật vậy:

$\sqrt{\left ( x-\frac{p}{2} \right )^{2}+y^{2}}=\left | x+\frac{p}{2} \right |$ $\Rightarrow$ MF = d(M, $\Delta $) 

Vậy M thuộc (P).

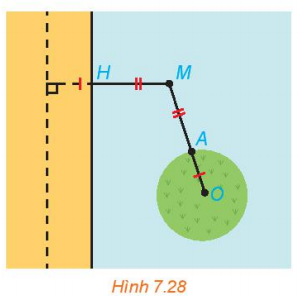
Vận dụng 2:  Tại một vùng biển giữa đất liền và một đảo, người ta phân định một đường ranh giới cách đều đất liền và đảo. Coi bờ biển vùng đất liền đó là một đường thẳng và đảo là hình tròn. Hỏi đường ranh giới nói trên có hình gì? Vì sao?

Hướng dẫn giải:

Coi đường đất liền là đường chuẩn, đảo là vị trí tiêu điểm F. Thì đường ranh giới là tập hợp các điểm cách đều đất liền và đảo là đường hình parabol. Vì thỏa mãn tính chất đường parabol, các điểm M nằm trên đường ranh giới cách đều đường chuẩn và tiêu điểm F.

4. MỘT SỐ ỨNG DỤNG CỦA BA ĐƯỜNG CONIC

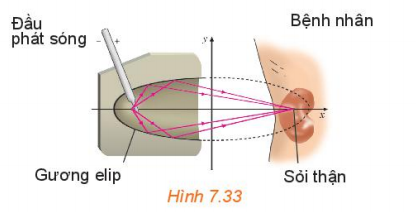
Vận dụng 3:  Gương elip trong một máy tán sỏi thận (H.7.33) ứng với elip có phương trình chính tắc $\frac{x^{2}}{400}+\frac{y^{2}}{76}=1$ (theo đơn vị cm). Tính khoảng cách từ vị trí đầu phát sóng của máy đến vị trí của sỏi thận cần tán.

Hướng dẫn giải:

Khoảng cách từ đầu phát sóng của máy đến vị trí của sỏi thận cần tán là tiêu cự.

Ta có: a² = 400, b² = 76, c = $\sqrt{a^{2}-b^{2}}=18$, nên tiêu cự là 2c = 36.

Vậy khoảng cách từ đầu phát sóng của máy đến vị trí của sỏi thận cần tán là 36 cm. 

=============
– Học Toán lớp 10 – Kết nối