Trả lời câu hỏi trong bài 19 Phương trình đường thẳng
=============
1. PHƯƠNG TRÌNH TỔNG QUÁT CỦA ĐƯỜNG THẲNG
Hoạt động 1: Cho vecto $\overrightarrow{n}\neq \overrightarrow{0}$ và điểm A. Tìm tập hợp những điểm M sao cho $\overrightarrow{AM}$ vuông góc với $\overrightarrow{n}$.
Hướng dẫn giải:
M nằm trên đường thẳng đi qua A và vuông góc với giá của vecto $\overrightarrow{n}$.
Hoạt động 2: Trong mặt phẳng tọa độ, cho đường thẳng $\Delta $ đi qua điểm A$(x_{o};y_{o})$ và có vecto pháp tuyển $\overrightarrow{n}(a;b)$. Chứng minh rằng điểm M(x; y) thuộc $\Delta $ khi và chỉ khi
$a(x-x_{o})+b(y-y_{o})=0$
Hướng dẫn giải:
- Giả sử M thuộc $\Delta $, ta chứng minh $a(x-x_{o})+b(y-y_{o})=0$
Thật vậy: Nếu M thuộc $\Delta $ thì $\overrightarrow{AM}\perp \overrightarrow{n}$
Có $\overrightarrow{AM}(x-x_{o}; y-y_{o})$
Suy ra: $\overrightarrow{AM}.\overrightarrow{n}=0$
$\Leftrightarrow $ $a(x-x_{o})+b(y-y_{o})=0$.
- Giả sử $a(x-x_{o})+b(y-y_{o})=0$, ta chứng minh M thuộc $\Delta $
Thật vậy: Nếu $a(x-x_{o})+b(y-y_{o})=0$ thì $\overrightarrow{AM}.\overrightarrow{n}=0$
Suy ra M thuộc đường thẳng đi qua A và vuông góc với giá của vecto $\overrightarrow{n}$.
Vậy M thuộc $\Delta $.
Luyện tập 1: Trong mặt phẳng tọa độ, cho tam giác có ba đỉnh A(-1; 5), B(2; 3), C(6; 1). Lập phương trình tổng quát của đường cao kẻ từ A của tam giác ABC.
Hướng dẫn giải:
Đường cao kẻ từ A của tam giác ABC nhận vecto $\overrightarrow{BC}$ làm vecto pháp tuyến.
$\overrightarrow{BC}(4; -2)$
Đường cao kẻ từ A của tam giác ABC có phương trình là:
4(x +1) – 2(y-5) = 0 hay 4x -2y +14 = 0.
Luyện tập 2: Hãy chỉ ra một vecto pháp tuyến của đường thẳng $\Delta $: y = 3x + 4.
Hướng dẫn giải:
Một vecto pháp tuyến là $\overrightarrow{n}(3; -1)$
2. PHƯƠNG TRÌNH THAM SỐ CỦA ĐƯỜNG THẲNG
Hoạt động 3: Trong Hình 7.2a, nếu một vật thể chuyển động với vecto vận tốc bằng $\overrightarrow{v}$ và đi qua A thì nó di chuyển trên đường nào?
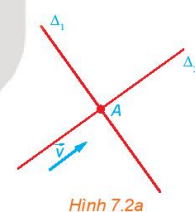
Hướng dẫn giải:
Di chuyển trên đường thẳng $\Delta_{2} $
Luyện tập 3: Hãy chỉ ra một vecto chỉ phương của đường thẳng $\Delta $: 2x – y +1 = 0
Hướng dẫn giải:
$\Delta $ có một vecto pháp tuyến là: $\overrightarrow{n}(2; -1)$
$\Rightarrow$ một vecto chỉ phương là: $\overrightarrow{u}(1; 2)$
Hoạt động 4: Chuyển động của một vật thể được thể hiện trên mặt phẳng Oxy. Vật thể khởi hành từ A(2; 1) và chuyển động thẳng đều với vecto vận tốc $\overrightarrow{v}(3; 4)$.
a. Hỏi vật thể chuyển động trên đường thẳng nào (chỉ ra điểm đi qua và vecto chỉ phương của đường thẳng đó)?
b. Chứng minh rằng, tại thời điểm t (t > 0) tính từ khi khởi hành, vật thể ở vị trí có tọa độ là (2+3t; 1 +4t).
Hướng dẫn giải:
a. Vật chuyên động trên đường thẳng đi qua A và song song với giá của vecto $\overrightarrow{v}(3; 4)$. Hay đường thẳng qua A và có vecto chỉ phương là $\overrightarrow{v}(3; 4)$.
b. Gọi tại thời điểm t vật ở điểm B(x; y).
Ta có: $\overrightarrow{AB} = t.\overrightarrow{v}$
$\Rightarrow$ $\left\{\begin{matrix}x-2=t.3\\ y-1=t.4\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}x=2+3t\\ y=1+4t\end{matrix}\right.$
$\Rightarrow$ tọa độ B((2+3t; 1 +4t) là vị trí của vật.
Luyện tập 4: Lập phương trình tham số của đường thẳng $\Delta $ đi qua điểm M(-1; 2) và song song với đường thẳng d: 3x – 4y -1 = 0.
Hướng dẫn giải:
Đường thẳng $\Delta $ song song với d: 3x – 4y -1 = 0.
$\Rightarrow$ $\Delta $ có vecto pháp tuyển: $\overrightarrow{n}(3; -4)$
$\Rightarrow$ $\Delta $ có vecto chỉ phương: $\overrightarrow{u}(4; 3)$
Phương trình tham số của $\Delta $ là:
$\left\{\begin{matrix}x=-1+4t\\ y=2+3t\end{matrix}\right.$
Luyện tập 5: Lập phương trình tham số và phương trình tổng quát của đường thẳng đi qua hai điểm phân biệt $A(x_{1}; y_{1}), B(x_{2}; y_{2})$ cho trước.
Hướng dẫn giải:
Đường thẳng có vecto chỉ phương $\overrightarrow{AB}(x_{2}-x_{1};y_{2}-y_{1})$
- Phương trình tham số của đường thẳng là:
$\left\{\begin{matrix}x=x_{1}+(x_{2}-x_{1})t\\ y=y_{1}+(y_{2}-y_{1})t\end{matrix}\right.$
- Đường thẳng có vecto pháp tuyến là: $\overrightarrow{n}(y_{1}-y_{2};x_{2}-x_{1})$
Phương trình tổng quát của đường thẳng là:
$(y_{1}-y_{2})(x-x_{1}) + (x_{2}-x_{1})(y – y_{1})=0$
Vận dụng: Việc quy đổi nhiệt độ giữa đơn vị độ C và đơn vị độ F được xác định bởi hai mốc sau:
- Nước đóng băng ở 0oC, 32oF;
- Nước sôi ở 100oC, 212oF.
Trong quy đổi đó, nếu aoC tương ứng với boF thì trên mặt phẳng tọa độ Oxy, điểm M(a; b) thuộc đường thẳng đi qua A(0; 32) và B(100; 212).
Hỏi 0oF, 100oF tương ứng với bao nhiêu độ C?
Hướng dẫn giải:
- Viết phương trình đường thẳng qua A và B.
Đường thẳng AB có vecto chỉ phương: $\overrightarrow{AB}(100; 180)$
$\Rightarrow$ chọn vecto chỉ phương $\overrightarrow{u}(5; 9)$
Phương trình tham số của đường thẳng AB:
$\left\{\begin{matrix}x=5t\\ y=32+9t\end{matrix}\right.$
- Nếu y = 0 thì x = $\frac{-160}{9}\approx -17, 78$
- Nếu y = 100 thì x = $\frac{340}{9}\approx 37, 78$
Vậy 0oF, 100oF lần lượt tương ứng với -17,78 và 37,78 độ C
=============
– Học Toán lớp 10 – Kết nối
