Trả lời câu hỏi trong bài 2 Định lí côsin và định lí sin – Chân trời

Trả lời câu hỏi trong bài 2 Định lí côsin và định lí sin – Chân trời
============

KHỞI ĐỘNG 

Làm thế nào để tính độ dài cạnh chưa biết của hai tam giác dưới đây?

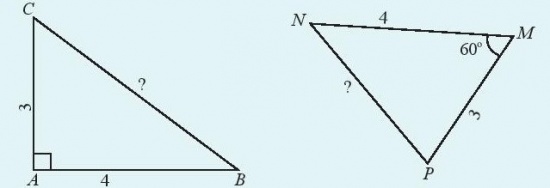
Hướng dẫn giải:

• Hình 1 sử dụng định lí Pytago: $BC^{2}$ = $AB^{2}$ + $AC^{2}$ = $3^{2}$ + $4^{2}$ $\Rightarrow$ BC = 5
• Hình 2 sử dụng định lí côsin trong tam giác: $NP^{2}$ = $MN^{2}$ + $MP^{2}$ – 2MN. MP. cosM = $4^{2}$ + $3^{2}$ – 2. 4. 3. cos$60^{\circ}$  $\Rightarrow$ NP = $\sqrt{13}$

1. ĐỊNH LÍ CÔSIN TRONG TAM GIÁC

Khám phá 1: 

a. Cho tam giác ABC không phải là tam giác vuông với góc A  nhọn và  $\widehat{C} \geq \widehat{B}$. Vẽ đường cao CD và đặt tên các độ dài như trong Hình 1.

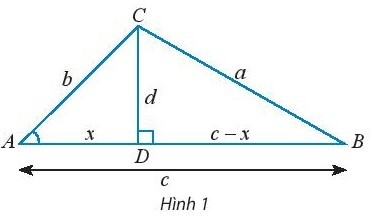
Hãy thay ? bằng chữ cái thích hợp để chứng minh công thức $a^{2} = b^{2} + c^{c} – 2bccosA$ theo gợi ý sau:

• Xét tam giác vuông BCD, ta có $a^{2} = d^{2} + (c – d)^{2}  = d^{2} + x^{2} + c^{2} – 2xc$. (1)
• Xét tam giác vuông ACD, ta có $b^{2} = d^{2} + x^{2} \Rightarrow d^{2} = b^{2} – x^{2}$.   (2)
• cosA = $\frac{?}{b}$ $\Rightarrow$ ? = bcosA.                                                                     (3)

Thay (2) và (3) vào (1), ta có: $a^{2} = b^{2} + c^{2} – 2bccosA$.

Lưu ý: Nếu $\widehat{B}$ > $\widehat{C}$ thì ta vẽ đường cao BD và chứng minh tương tự.

b. Cho tam giác ABC với góc A tù. Làm tương tự như trên, chứng minh rằng ta cũng có:

$a^{2} = b^{2} + c^{2} – 2bccosA$.

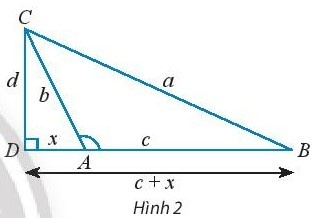
Lưu ý: Vì A là góc tù nên cosA = $-\frac{x}{b}$.

c. Cho tam giác ABC vuông tại A. Hãy chứng tỏ công thức $a^{2} = b^{2} + c^{2} – 2bccosA$ có thể viết là $a^{2} = b^{2} + c^{2}$.

Hướng dẫn giải:

a. cosA = $\frac{x}{b}$ $\Rightarrow$ x = bcosA.

b. Xét tam giác CDB vuông tại D, ta có: $a^{2} = d^{2} + (c + x)^{2}$                                           (4)

Xét tam giác CDA vuông tại D, ta có: $b^{2} = d^{2} + x^{2} \Rightarrow d^{2} = b^{2} – x^{2}$    (5)

cos$\widehat{BAC}$ = -cos$\widehat{CAD}$ = $-\frac{x}{b}$ $\Rightarrow$ x = -bcosA               (6)

Thay (5), (6) vào (4), ta có: $a^{2} = b^{2} + c^{2} – 2bccosA$.

c. Tam giác ABC vuông tại A $\Rightarrow$ $\widehat{A}$ = $90^{\circ}$

Ta có: $a^{2} = b^{2} + c^{2} – 2bccosA$ $\Leftrightarrow$  $a^{2} = b^{2} + c^{2} – 2bccos90^{\circ}$ $\Leftrightarrow$ $a^{2} = b^{2} + c^{2}$

Thực hành 1:  Tính các cạnh và các góc chưa biết của tam giác ABC trong Hình 4. 

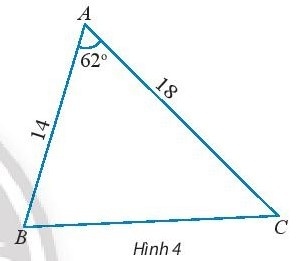
Hướng dẫn giải:

Theo định lí côsin, ta có:

$BC^{2} = AB^{2} + AC{2} – 2AB. AC. cosA$ = $14^2 + 18^{2} – 2. 14. 18. cos62^{\circ}$ $\approx$ 283,39

Vậy BC $\approx$  $\sqrt{283,39} \approx$ 16,83

Vận dụng 1:  Tính khoảng cách giữa hai điểm ở hai đầu của một hồ nước. Biết từ một điểm cách hai đầu hồ lần lượt là 800 m và 900 m người quan sát nhìn hai điểm này dưới một góc $70^{\circ}$ (Hình 5).

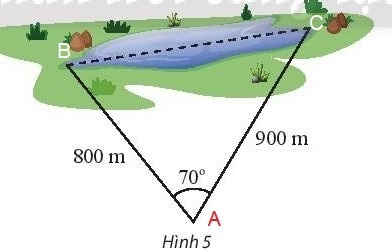
Hướng dẫn giải:

Gọi các đỉnh của tam giác như trong hình vẽ:

Ta có: $BC^{2} = AB^{2} + AC^{2} – 2AB. AC. cosA = 800^{2} + 900^{2} – 800. 900. cos70^{\circ}$ = 1203745,497

 $\Rightarrow$ BC $\approx$ 1097,15 (m)

Vậy khoảng cách giữa hai điểm là 1097,15m.

2. ĐỊNH LÍ SIN TRONG TAM GIÁC

Khám phá 2:

a. Cho tam giác ABC không phải là tam giác vuông có BC = a, AC = b, AB = c và R là bán kính đường tròn ngoại tiếp tam giác đó. Vẽ đường kính BD.

i. Tính sin$\widehat{BDC}$ theo a và R.

ii. Tìm mối liên hệ giưa $\widehat{BAC}$ và $\widehat{BDC}$. Từ đó chứng minh rằng 2R = $\frac{a}{sinA}$

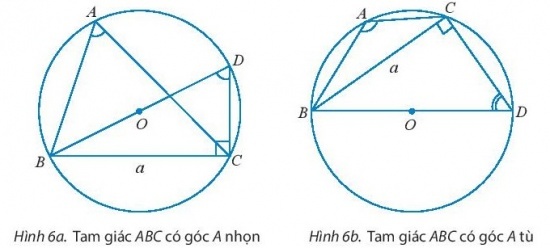
b. Cho tam giác ABC với góc A vuông. Tính sinA và so sánh a với 2R để chứng tỏ ta vẫn có công thức 2R = $\frac{a}{sinA}$

Hướng dẫn giải:

a.

i. Xét tam giác BDC vuông tại C ta có:

sin$\widehat{BDC}$ = $\frac{BC}{2R}$ = $\frac{a}{2R}$

ii. Với tam giác ABC có góc A nhọn, ta có: $\widehat{BAC}$ = $\widehat{BDC}$ (hai góc nội tiếp cùng chắn cung BC).

$\Rightarrow$ sin$\widehat{BAC}$ = sin$\widehat{BDC}$ = $\frac{BC}{2R}$ = $\frac{a}{2R}$ $\Rightarrow$ 2R = $\frac{a}{sinA}$ (đpcm)

Với tam giác ABC có góc A tù, ta có tứ giác ACDB nội tiếp đường tròn tâm O $\Leftrightarrow$ $\widehat{BAC}$ + $\widehat{BDC}$ = $180^{\circ}$ 

$\Rightarrow$ sin$\widehat{BAC}$ = sin$\widehat{BDC}$ = $\frac{BC}{2R}$ = $\frac{a}{2R}$ $\Rightarrow$ 2R = $\frac{a}{sinA}$ (đpcm)

b. Tam giác ABC vuông tại A nội tiếp đường tròn tâm O bán kính $\frac{BC}{2}$ $\Rightarrow$ 2R = a (1)

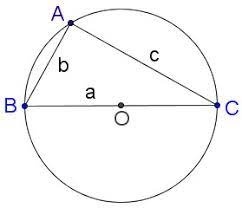
Ta có: sinA = sin$90^{\circ}$ = 1 (2)

Từ (1) và (2) $\Rightarrow$ 2R = $\frac{a}{sinA}$

Thực hành 2:  Tính các cạnh và các góc chưa biết của tam giác MNP trong Hình 8.

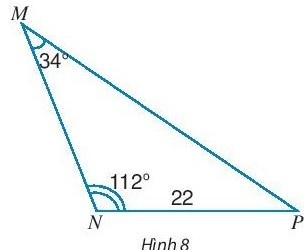
Hướng dẫn giải:

Ta có:  $\widehat{P}$ = $180^{\circ}$ – $34^{\circ}$ – $112^{\circ}$ = $34^{\circ}$ $\Rightarrow$ tam giác MNP cân tại N $\Rightarrow$ MN = NP = 22

Áp dụng định lí sin, ta có: $\frac{NP}{sinM}$ = $\frac{MP}{sinN}$ = $\frac{MN}{sinP}$ = 2R

Suy ra:

MP = $\frac{NP.sinN}{sinM}$ = $\frac{22.sin112^{\circ}}{sin34^{\circ}}$ $\approx$ 36,5

Vận dụng 2:  Trong một khu bảo tồn, người ta xây dựng một tháp canh và hai bồn chứa nước A, B để phòng hỏa hoạn. Từ tháp canh, người ta phát hiện đám cháy và số liệu đưa về như hình 9. Nên dẫn nước từ bồn chứa A hay B để dập tắt đám cháy nhanh hơn?

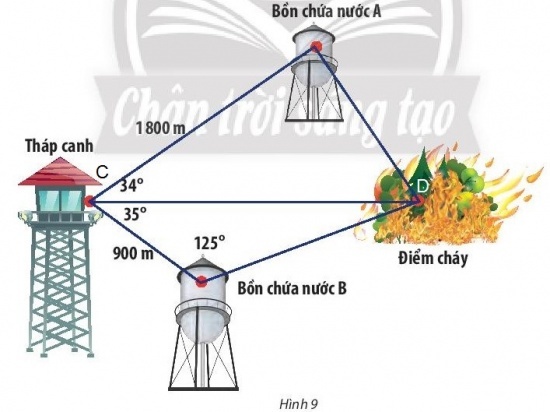
Hướng dẫn giải:

Gọi điểm tháp canh là C, điểm cháy là D (như hình vẽ).

Ta có: $\widehat{BDC}$ = $180^{\circ}$ – $35^{\circ}$ – $125^{\circ}$ = $20^{\circ}$ 

Áp dụng định lí sin cho tam giác CBD ta có: 

$\frac{BD}{sin\widehat{BCD}}$ = $\frac{CB}{sin\widehat{BDC}}$ = $\frac{CD}{sin\widehat{CBD}}$ = 2R

Suy ra: BD = $\frac{CB.sin\widehat{BCD}}{sin\widehat{BDC}}$ = $\frac{900. sin35^{\circ}}{sin20^{\circ}}$ $\approx$ 1509,3 (m)

CD = $\frac{CB.sin\widehat{CBD}}{sin\widehat{BDC}}$ = $\frac{900. sin125^{\circ}}{sin20^{\circ}}$ $\approx$ 2155,5 (m)

Áp dụng định lí cosin trong tam giác ACD, ta có:

$AD^{2} = CA^{2} + CD^{2} – 2AC. CD. cos\widehat{ACD}$ = $1800^2 + 2155,5^{2} – 2. 1800. 2155,5. cos34^{\circ}$ $\approx$ 1453014,5

$\Rightarrow$ AD $\approx$ 1205,4 (m)

Nhận thấy: AD < BD nên dẫn nước từ bồn chứa A sẽ dập tắt đám cháy nhanh hơn.

3. CÁC CÔNG THỨC TÍNH DIỆN TÍCH TAM GIÁC

Khám phá 3:  Cho tam giác như Hình 10.

a. Viết công thức tính diện tích S của tam giác ABC theo a và $h_{a}$.

b. Tính $h_{a}$ theo b và sinC.

c. Dùng hai kết quả trên để chứng minh công thức S = $\frac{1}{2}$ab.sinC.

d. Dùng định lí sin và kết quả ở câu c) để chứng minh công thức S = $\frac{abc}{4R}$

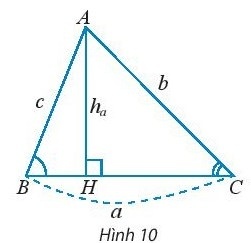
Hướng dẫn giải:

a. Xét tam giác ABC, đường cao AH:

$S_{ABC}$ = $\frac{1}{2}$. AH. BC = $\frac{1}{2}$. $h_{a}$.a (1)

b. Xét tam giác AHC vuông tại H, ta có:

sinC = $\frac{AH}{AC}$ = $\frac{h_{a}}{b}$ $\Rightarrow$ $h_{a}$ = b.sinC (2)

c. Thay (2) vào (1) ta được: S = $\frac{1}{2}$absinC.

d. Áp dụng định lí sin ta có: $\frac{a}{sinA}$ = $\frac{b}{sinB}$ = $\frac{c}{sinC}$ = 2R

$\Rightarrow$ sinC = $\frac{c}{2R}$

$\Rightarrow$ S = $\frac{1}{2}$absinC = $\frac{1}{2}ab.\frac{c}{2R}$ $\Rightarrow$ S = $\frac{abc}{4R}$ (đpcm)

Khám phá 4:  Cho tam giác ABC có BC = a, AC = b, AB = c và (1; r) là đường tròn nội tiếp tam giác (Hình 11).

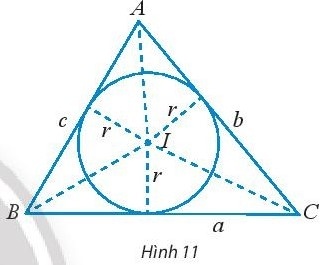
a. Tính diện tích các tam giác IBC, IAC, IAB theo r và a, b, c.

b. Dùng kết quả trên để chứng minh công thức tính diện tích tam giác ABC: S = $\frac{r(a+b+c)}{2}$

Hướng dẫn giải:

a. $S_{IBC}$ = $\frac{1}{2}$. r. a;    $S_{IAC}$ = $\frac{1}{2}$. r. b;   $S_{IAB}$ = $\frac{1}{2}$. r. c

b. $S_{ABC}$ = $S_{IBC}$ + $S_{IAC}$ + $S_{IAB}$ = $\frac{1}{2}$. r. a + $\frac{1}{2}$. r. b + $\frac{1}{2}$. r. c 

$\Rightarrow$ S = $\frac{r(a+b+c)}{2}$ (đpcm)

Thực hành 3:  Tính diện tích tam giác ABC và bán kính đường tròn ngoại tiếp tam giác ABC trong các trường hợp sau:

a. Các cạnh b = 14, c = 35 và  $\widehat{A}$ = $60^{\circ}$

b. Cách cạnh a = 4, b = 5, c = 3.

Hướng dẫn giải:

a. S = $\frac{1}{2}$bcsinA = $\frac{1}{2}$14. 35. sin$60^{\circ}$ = $\frac{245\sqrt{3}}{2}$

Áp dụng định lí cosin, ta có:

$a^{2} = b^{2} + c^{2} – 2bccosA$ = $14^{2} + 35^{2} – 2. 14. 35. cos60^{\circ}$ = 931

$\Rightarrow$ a = $7\sqrt{19}$

Áp dụng định lí sin, ta có: R = $\frac{a}{2.sinA}$ = $\frac{7\sqrt{19}}{2.sin60^{\circ}}$ = $\frac{7\sqrt{57}}{3}$

b. Ta có: p = $\frac{1}{2}$.(4 + 5 + 3) = 6

Áp dụng công thức Heron, ta có:

S = $\sqrt{p(p – a)(p – b)(p – c)}$ = $\sqrt{6.(6 – 4).(6 – 5). (6 – 3)}$ = 6

Ta có: S = $\frac{abc}{4R}$ $\Rightarrow$ R = $\frac{abc}{4S}$ = $\frac{4.5.3}{4.6}$ = $\frac{5}{2}$ 

Vận dụng 3:  Tính diện tích một cánh buồm hình tam giác. Biết cánh buồm đó có chiều dài cạnh là 3,2m và hai góc kề cạnh đó có số đo là $48^{\circ}$ và $105^{\circ}$ (Hình 12)

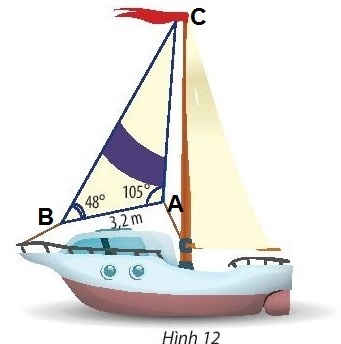
Hướng dẫn giải:

Chọn các đỉnh A, B, C như hình.

Ta có: $\widehat{C}$ = $180^{\circ}$ – $48^{\circ}$ = $27^{\circ}$

Áp dụng định lí sin, ta có: $\frac{BC}{sinA}$ = $\frac{AB}{sinC}$ = $\frac{AC}{sinB}$ = 2R

$\Rightarrow$ BC = $\frac{AB. sinA}{sinC}$ = $\frac{3,2. sin48^{\circ}}{sin27^{\circ}}$ $\approx$ 5,2 (m)

S = $\frac{1}{2}$AB. BC. sinB $\approx$ $\frac{1}{2}$. 3,2. 5,2. sin$48^{\circ}$ $\approx$ 6,2 ($m^{2}$)

===========
Chuyên mục: Học Toán lớp 10 – Chân trời