Lý thuyết Bài 1: Giá trị lượng giác của một góc từ 0˚ đến 180˚ – Chân trời
============
1.1. Giá trị lượng giác
|
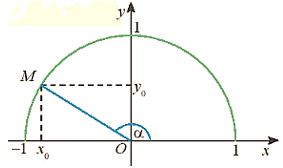
+) Với mỗi góc \(\alpha ({0^o} \le \alpha \le {180^o})\) có duy nhất điểm \(M({x_0};{y_0})\) trên nửa đường tròn đơn vị để \(\widehat {xOM} = \alpha .\) Khi đó: \(\sin \alpha = {y_0}\) là tung độ của M \(\cos \alpha = {x_0}\) là hoành độ của M \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{{y_0}}}{{{x_0}}}(\alpha \ne {90^o})\) \(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{{{x_0}}}{{{y_0}}}(\alpha \ne {0^o},\alpha \ne {180^o})\) |
|---|
Ví dụ: Tìm các giá trị lượng giác của góc 120°.
Giải
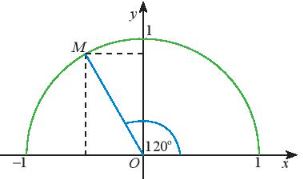
Lấy điểm M trên nửa đường tròn đơn vị sao cho.
\(\widehat {xOM} = {120^0}\). Ta có \(\widehat {MOy} = {120^0} – {90^0} = {30^0}\).
Ta tính được toạ độ điểm M là \(\left( { – \frac{1}{2};\frac{{\sqrt 3 }}{2}} \right)\)
Vậy theo định nghĩa ta có:
\(\begin{array}{l}
\sin {120^0} = \frac{{\sqrt 3 }}{2};cos{120^0} = – \frac{1}{2};\\
\tan {120^0} = – \sqrt 3 ;\cot {120^0} = – \frac{{\sqrt 3 }}{3}.
\end{array}\)
Chú ý:
a) Nếu \(\alpha\) là góc nhọn thì các giá trị lượng giác của \(\alpha\) đều dương
Nếu ơ là góc tù thì sin\(\alpha\) > 0, cos\(\alpha\) < 0, tan\(\alpha\) < 0, cot\(\alpha\) < 0.
b) tan\(\alpha\) chỉ xác định khi \(\alpha \ne {90^0}\).
cot\(\alpha\) chỉ xác định khi \(\alpha \ne {0^0}\) và \(\alpha \ne {180^0}\).
1.2. Quan hệ giữa các giá trị lượng giác của hai góc bù nhau
Hai góc bù nhau, \(\alpha \) và \({180^o} – \alpha \) :
| \(\begin{array}{l}\sin \left( {{{180}^o} – \alpha } \right) = \sin \alpha \\\cos \left( {{{180}^o} – \alpha } \right) = – \cos \alpha \\\tan \left( {{{180}^o} – \alpha } \right) = – \tan \alpha (\alpha \ne {90^o})\\\cot \left( {{{180}^o} – \alpha } \right) = – \cot \alpha ({0^o} < \alpha < {180^o})\end{array}\) |
|---|
Hai góc phụ nhau, \(\alpha \) và \({90^o} – \alpha \) :
| \(\begin{array}{l}\sin \left( {{{90}^o} – \alpha } \right) = \cos \alpha \\\cos \left( {{{90}^o} – \alpha } \right) = \sin \alpha \\\tan \left( {{{90}^o} – \alpha } \right) = \cot \alpha (\alpha \ne {90^o},{0^o} < \alpha < {180^o})\\\cot \left( {{{90}^o} – \alpha } \right) = \tan \alpha (\alpha \ne {90^o},{0^o} < \alpha < {180^o})\end{array}\) |
|---|
Ví dụ: Cho biết \(\sin {30^0} = \frac{1}{2};cos{45^0} = \frac{{\sqrt 2 }}{2};\tan {60^0} = \sqrt 3 \). Tính \(\sin {150^0};cos{135^0};\tan {120^0}.\)
Giải
\(\begin{array}{l}
\sin {150^0} = \sin \left( {{{180}^0} – {{30}^0}} \right) = \sin {30^0} = \frac{1}{2};\\
cos{135^0} = – cos{45^0} = – \frac{{\sqrt 2 }}{2};\\
\tan {120^0} = – \tan {60^0} = – \sqrt 3 .
\end{array}\)
1.3. Giá trị lượng giác của một số góc đặc biệt
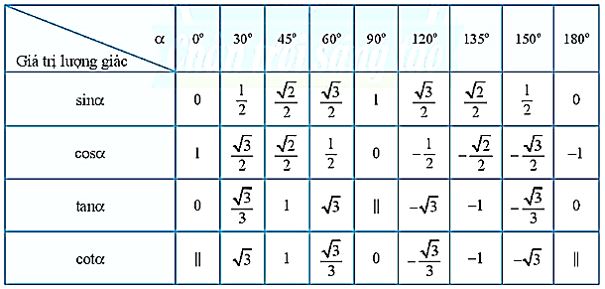
Chú ý: Trong bảng, kí hiệu “||” để chỉ giá trị lượng giác không xác định.
1.4. Sử dụng máy tính cầm tay để tính giá trị lượng giác của một góc
a) Tính các giá trị lượng giác của góc
Bước 1: Cài đặt đơn vị đo góc (độ hoặc radian)
Bước 2: Vào chế độ tính toán
Chú ý: Để tính \(\cot \alpha \) ta tính \(\frac{1}{{\tan \alpha }}\).
b) Xác định số đo của góc khi biết giá trị lượng giác của góc đó
Để tìm \(\alpha \) khi biết \(\cot \alpha \) ta tính \(\tan \alpha = \frac{1}{{\cot \alpha }}\) rồi tính \(\alpha \) sau.
Câu 1: Tính các giá trị lượng giác: \(\sin {120^o};\cos {150^o};\cot {135^o}.\)
Hướng dẫn giải
\(\begin{array}{l}\sin {120^o} = \sin \;({180^o} – {60^o}) = \sin {60^o} = \frac{{\sqrt 3 }}{2};\\\cos {150^o} = – \cos \;({180^o} – {30^o}) = – \cos {30^o} = – \frac{{\sqrt 3 }}{2};\\\cot {135^o} = – \cot \;({180^o} – {45^o}) = – \cot {45^o} = – 1.\end{array}\)
Câu 2: Cho biết \(\sin \alpha = \frac{1}{2},\) tìm góc \(\alpha \;({0^o} \le \alpha \le {180^o})\) bằng cách vẽ nửa đường tròn đơn vị.
Hướng dẫn giải
Gọi M là điểm thuộc nửa đường tròn đơn vị sao cho: \(\widehat {xOM} = \alpha \)
Do \(\sin \alpha = \frac{1}{2}\) nên tung độ của M bằng \(\frac{1}{2}.\)
Vậy ta xác định được hai điểm N và M thỏa mãn \(\sin \widehat {xON} = \sin \widehat {xOM} = \frac{1}{2}\)
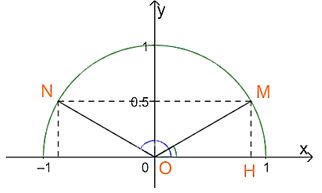
Đặt \(\beta = \widehat {xOM} \Rightarrow \widehat {xON} = {180^o} – \beta \)
Xét tam giác OHM vuông tại H ta có: \(MH = \frac{1}{2} = \frac{{OM}}{2} \Rightarrow \beta = {30^o}\)
\( \Rightarrow \widehat {xON} = {180^o} – {30^o} = {150^o}\)
Vậy \(\alpha = {30^o}\) hoặc \(\alpha = {150^o}\)
Câu 3: Tính:
\(A = \sin {150^o} + \tan {135^o} + \cot {45^o}\)
\(B = 2\cos {30^o} – 3\tan 150 + \cot {135^o}\)
Hướng dẫn giải
\(A = \sin {150^o} + \tan {135^o} + \cot {45^o}\)
Sử dụng bảng giá trị lượng giác của một số góc đặc biệt, ta có:
\(\sin {150^o} = \frac{1}{2};\tan {135^o} = – 1;\cot {45^o} = 1.\)
\( \Rightarrow A = \frac{1}{2} – 1 + 1 = \frac{1}{2}.\)
\(B = 2\cos {30^o} – 3\tan 150 + \cot {135^o}\)
Sử dụng bảng giá trị lượng giác của một số góc đặc biệt, ta có:
\(\cos {30^o} = \frac{{\sqrt 3 }}{2};\tan {150^o} = – \frac{{\sqrt 3 }}{3};\cot {135^o} = – 1.\)
\( \Rightarrow B = 2.\frac{{\sqrt 3 }}{2} – 3.\left( { – \frac{{\sqrt 3 }}{3}} \right) + 1 = 5\sqrt 3 + 1.\)
Câu 4: Tìm góc \(\alpha ({0^o} \le \alpha \le {180^o})\) trong mỗi trường hợp sau:
a) \(\sin \alpha = \frac{{\sqrt 3 }}{2}\)
b) \(\cos \alpha = \frac{{ – \sqrt 2 }}{2}\)
Hướng dẫn giải
a) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \(\sin \alpha \) ta có:
\(\sin \alpha = \frac{{\sqrt 3 }}{2}\) với \(\alpha = {60^o}\) và \(\alpha = {120^o}\)
b) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng \(\cos \alpha \) ta có:
\(\cos \alpha = \frac{{ – \sqrt 2 }}{2}\) với \(\alpha = {135^o}\)
===========
Chuyên mục: Chương 4: Hệ thức lượng trong tam giác
