Lý thuyết Bài 2: Định lí cosin và định lí sin – Chân trời

Lý thuyết Bài 2: Định lí cosin và định lí sin – Chân trời
============

1.1.  Định lí cosin trong tam giác

Ví dụ:  Cho tam giác ABC có \(\widehat C = {115^0},AC = 8\) và BC = 12. Tính độ dài cạnh AB và các góc A, B của tam giác đó. 

Giải

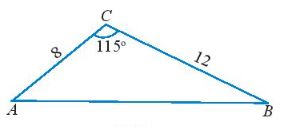
Theo định lí côsin, ta có: 

\(\begin{array}{l}
A{B^2} = B{C^2} + A{C^2} – 2.BC.AC.\cos C\\
 = {12^2} + {8^2} – 2.12.8.cos{115^0}\\
 \approx 289,14
\end{array}\)

Vậy \(AB \approx \sqrt {289,14}  \approx 7\) 

1.2.  Định lí sin trong tam giác

Ví dụ: Cho tam giác ABC có \(\widehat A = {72^0},\widehat B = {83^0},BC = 18\). Tính độ dài các cạnh AC, AB và bán kính R của đường tròn ngoại tiếp tam giác đỏ.

Giải

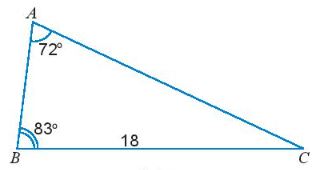
Đặt a= BC, b =AC, c =AB

Ta có: \(a = 18,\widehat C = {180^0} – \left( {{{72}^0} + {{83}^0}} \right) = {25^0}\)

Áp dụng định lí sin, ta có: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\)

Suy ra

\(\begin{array}{l}
AC = b = \frac{{asinB}}{{\sin A}} = \frac{{18.\sin {{83}^0}}}{{\sin {{72}^0}}} \approx 18,8\\
AB = c = \frac{{a\sin C}}{{\sin A}} = \frac{{18.\sin {{25}^0}}}{{\sin {{72}^0}}} \approx 8\\
R = \frac{a}{{2.\sin A}} = \frac{{18}}{{2.\sin {{72}^0}}} \approx 9,5
\end{array}\)

1.3. Các công thức tính diện tích tam giác

1) \(S = \frac{1}{2}a{h_a} = \frac{1}{2}b{h_b} = \frac{1}{2}c{h_c}\)

2) \(S = \frac{1}{2}bc\sin A = \frac{1}{2}ca\sin B = \frac{1}{2}ab\sin C\)

3) \(S = \frac{{abc}}{{4R}}\)

4) \(S = pr = \frac{{(a + b + c).r}}{2}\)

5) \(S = \sqrt {p(p – a)(p – b)(p – c)} \) (Công thức Heron)

Ví dụ:  Cho tam giác 48C có các cạnh a = 30, b =26, e =28.

a) Tính diện tích tam giác 48C.

b) Tính bán kính đường tròn ngoại tiếp và bản kinh đường tròn nội tiếp tam giác ⁄48C.

Giải

a) Ta có: \(p = \frac{1}{2}.\left( {30 + 26 + 28} \right) = 42\)

Áp dụng công thức Heron, ta có:

\(S = \sqrt {p\left( {p – a} \right)\left( {p – b} \right)\left( {p – c} \right)}  = \sqrt {42\left( {42 – 30} \right)\left( {42 – 26} \right)\left( {42 – 28} \right)}  = 336\)

b) Ta có: \(S = \frac{{abc}}{{4R}}\), suy ra \(R = \frac{{abc}}{{4S}} = \frac{{30.26.28}}{{4.336}} = 16,25\)

Ta lại có S = pr, Suy ra \(r = \frac{S}{p} = \frac{{336}}{{42}} = 8\) 

Câu 1:  Tính các cạnh và các góc chưa biết của tam giác ABC trong hình sau.

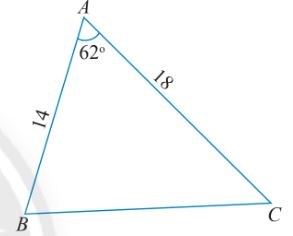
Hướng dẫn giải

Áp dụng định lí cosin trong tam giác ABC, ta có:

\(B{C^2} = A{C^2} + A{B^2} – 2AC.AB\cos A\)

Mà \(AB = 14,AC = 18,\widehat A = {62^o}\)

\(\begin{array}{l} \Rightarrow B{C^2} = {18^2} + {14^2} – 2.18.14\cos {62^o} \approx 283,3863\\ \Leftrightarrow BC \approx 16,834\end{array}\)

Lại có: Từ định lí cosin ta suy ra:

\(\cos B = \frac{{A{B^2} + B{C^2} – A{C^2}}}{{2.AB.BC}};\cos C = \frac{{A{C^2} + B{C^2} – A{B^2}}}{{2.AC.BC}}\)

\( \Rightarrow \left\{ \begin{array}{l}\cos B = \frac{{{{14}^2} + 16,{{834}^2} – {{18}^2}}}{{2.14.16,834}} \approx 0,3297\\\cos C = \frac{{{{18}^2} + 16,{{834}^2} – {{14}^2}}}{{2.18.16,834}} \approx 0,6788\end{array} \right.\)

\( \Rightarrow \left\{ \begin{array}{l}\widehat B \approx {70^o}45’\\\widehat C \approx {47^o}15’\end{array} \right.\)

Vậy \(BC \approx 16,834;\widehat B \approx {70^o}45′;\widehat C \approx {47^o}15′.\)

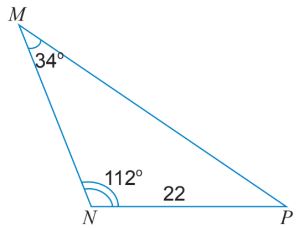
Câu 2:  Tính các cạnh và các góc chưa biết của tam giác MNP trong Hình sau.

Hướng dẫn giải

Ta có: \(NP = 22,\;\widehat P = {180^o} – ({112^o} + {34^o}) = {34^o}\)

Áp dụng định lí sin, ta có:

\(\frac{{MN}}{{\sin P}} = \frac{{MP}}{{\sin N}} = \frac{{NP}}{{\sin M}}\)

Suy ra:

\(MP = \frac{{NP.\sin N}}{{\sin M}} = \frac{{22.\sin {{112}^o}}}{{\sin {{34}^o}}} \approx 36,48\)

\(MN = \frac{{NP.\sin P}}{{\sin M}} = \frac{{22.\sin {{34}^o}}}{{\sin {{34}^o}}} = 22.\)

Câu 3: Tính diện tích tam giác ABC và bán kính đường tròn ngoại tiếp tam giác ABC trong các trường hợp sau:

a) Các cạnh \(b = 14,c = 35\) và \(\widehat A = {60^o}\)

b) Các cạnh \(a = 4,b = 5,c = 3\)

Hướng dẫn giải

a) Áp dụng công thức: \(S = \frac{1}{2}bc\sin A\), ta có:

\(S = \frac{1}{2}.14.35.\sin {60^o} = \frac{1}{2}.14.35.\frac{{\sqrt 3 }}{2} \approx 212,2\)

b) Ta có: \(p = \frac{1}{2}.(4 + 5 + 3) = 6\)

Áp dụng công thức Heron, ta có:

\(S = \sqrt {p(p – a)(p – b)(p – c)}  = \sqrt {6(6 – 4)(6 – 5)(6 – 3)}  = 6.\) 

===========
Chuyên mục: Chương 4: Hệ thức lượng trong tam giác