Sách Toán - Học toán
Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán
Đề bài Câu 1: Hàm số \(F(x) = {e^{3x}}\) là một nguyên hàm của hàm số: A.\(f(x) = 3{e^{3x}}.\) B.\(f(x) = {e^{3x}}.\) C.\(f(x) = \dfrac{{{e^{3x}}}}{3}.\) D.\(f(x) = 3\ln 3x.\) Câu 2: Trên khoảng \((0; + \infty )\) thì hàm số \(y = - {x^3} + 3x + 1\) A. có giá trị nhỏ nhất là -1. B. có giá trị lớn nhất là – 1. C. có giá trị lớn … [Đọc thêm...] vềĐề thi HK2 Toán 12 – Tham khảo số 4 – 2019
Đề bài Câu 1: Cho f(x) và g(x) là hai hàm liên tục trên \(\left[ { - 1;1} \right]\) và f(x) là hàm số chẵn , g(x) là hàm số lẻ. Biết \(\int\limits_0^1 {f(x)dx} = 5\) và \(\int\limits_0^1 {g(x)dx} = 7\). Mệnh đề nào dưới đây là sai? A.\(\int\limits_{ - 1}^1 {\left[ {f(x) + g(x)} \right]dx} = 10.\) B.\(\int\limits_{ - 1}^1 {\left[ {f(x) - g(x)} \right]dx} = … [Đọc thêm...] vềĐề thi HK2 Toán 12 – Tham khảo số 2 – 2019
Đề bài Câu 1: Trong không gian với hệ trục tọa độ \(Oxyz\), gọi \((P)\)là mặt phẳng song song với mặt phẳng \(Oxz\) và cắt mặt cầu \({(x - 1)^2} + {(y + 2)^2} + {z^2} = 12\)theo đường tròn có chu vi lớn nhất. Phương trình của \((P)\) là: A.\(x - 2y + 1 = 0\). B.\(y - 2 = 0\). C.\(y + 1 = 0\). D.\(y + 2 = 0\). Câu 2: Trong không gian với hệ trục … [Đọc thêm...] vềĐề Kiểm Tra 1 tiết chương 3 Hình học 12 – Đề 3
Đề bài Câu 1: Trong không gian \(Oxyz\) cho ba điểm \(A( - 1; - 2;3),B(0;3;1),C(4;2;2)\). Cosin của góc \(\widehat {BAC}\) là A. \(\frac{9}{{2\sqrt {35} }}\). B. \(\frac{9}{{\sqrt {35} }}\). C. \( - \frac{9}{{2\sqrt {35} }}\). D. \( - \frac{9}{{\sqrt {35} }}\). Câu 2: Tọa độ của vecto \(\overrightarrow n \) vuông góc với hai vecto … [Đọc thêm...] vềĐề Kiểm Tra 1 tiết chương 3 Hình học 12 – Đề 1
Tỷ số thể tích khối đa diện Công thức tỉ số thể tích của khối chóp tam giác: Trên các đường thẳng SA, SB, SC của hình chóp S.ABC ta lấy lần lượt các điểm A', B', C'. Ta có: $\frac{{{V_{S.A'B'C'}}}}{{{V_{S.ABC}}}} = \frac{{SA'}}{{SA}}.\frac{{SB'}}{{SB}}.\frac{{SC'}}{{SC}}.$ Ví dụ 1: Cho hình chóp S.ABC có tam giác ABC đều cạnh 2a, cạnh bên SA vuông góc với … [Đọc thêm...] vềTỷ số thể tích khối đa diện
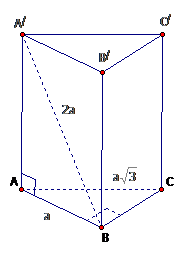
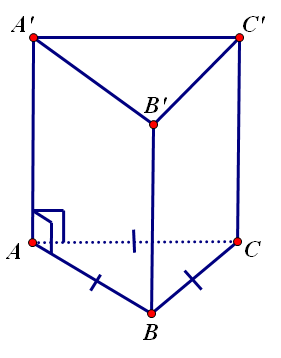
Thể tích khối lăng trụ LÝ THUYẾT Thể tích của khối lăng trụ bằng tích số của diện tích mặt đáy với chiều cao của khối lăng trụ đó: \(V=B.h.\) (trong đó B là diện tích đáy, h là chiều cao của khối lăng trụ) \(V=S_{day}.h.\) \(V_{ABC.A’B’C’}=S_{ABC}.C’H\) Để tính thể tích của khối lăng trụ ta cần đi tính chiều cao của lăng trụ và diện tích đáy. Các … [Đọc thêm...] vềThể tích khối lăng trụ
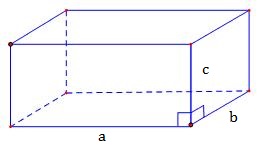
1. Tính chất của thể tích khối đa diện Hai khối đa diện bằng nhau thì có thể tích bằng nhau. Nếu 1 khối đa diện được phân chia thành các khối đa diện nhỏ thì thể tích của nó bằng tổng thể tích của các khối đa diện nhỏ. Khối lập phương có cạnh bằng 1 thì có thể tích bằng 1. 2. Thể tích khối hộp chữ nhật Giả sử có 1 khối hộp chữ nhật với 3 kích thước a, b, c đều là … [Đọc thêm...] vềLý thuyết thể tích của khối đa diện
Lý thuyết Khái niệm về khối đa diện 1) Khối lăng trụ Hình lăng trụ: 2 đáy là 2 đa giác bằng nhau. Các cạch bên song song và bằng nhau. Các mặt bên là các hình bình hành. Khối lăng trụ là phần không gian giới hạn bởi hình lăng trụ. Hình lăng trụ đứng: Định nghĩa: Hình lăng trụ đứng là hình lăng trụ có các cạnh bên vuông góc với mặt … [Đọc thêm...] vềLý thuyết Khái niệm về khối đa diện
I)Nhắc lại kiến thức cần nhớ: 1)Hệ thức lượng trong tam giác vuông: 2)Tỉ số lượng giác 3)Hệ thức về cạnh và góc trong tam giác vuông: 4)Đường tròn: -Trong phần này thì bao gồm nhiều phần trong đó trọng tâm sẽ là: +Các góc với đường tròn: góc nội tiếp, góc tạo bởi tiếp tuyến dây cung,.. +Chứng minh tứ giác nội tiếp(Đây là phần mà chắc chắn trong đề thi tuyển sinh vào lớp … [Đọc thêm...] vềChuyên đề 5: Hình học
I)Kiến thức cần nhớ: -Hiều đề,vững các phép biến đổi biểu thức để có thể biểu diễn ẩn và giải phương trình hoặc hệ phương trình. *Phương pháp giải: Bước 1: Lập phương trình hoặc hệ phương trình: -Chọn ẩn số,đặt điều kiện của ẩn số. -Biểu diễn các đại lượng đề bài theo ẩn số. -Lập phương trình hoặc hệ phương trình để biểu thị mối quan hệ giữa các đại lượng của đề … [Đọc thêm...] vềChuyên đề 4: Giải bài toán bằng cách lập phương trình,hệ phương trình và các bài toán thực tế
