Lý thuyết Bài 2: Hàm số bậc hai – Chân trời

Lý thuyết Bài 2: Hàm số bậc hai – Chân trời
============

1.1. Hàm số bậc hai

+ Định nghĩa: Hàm số bậc hai biến x là hàm số cho bởi công thức dạng \(y = f(x) = a{x^2} + bx + c\) với \(a,b,c \in \mathbb{R};a \ne 0.\) + Tập xác định: \(\mathbb{R}\)

Ví dụ: Hàm số nào trong các hàm số sau đâylà hàm số bậc hai?

\(\begin{array}{l}
a)y = 2{x^2} + x\\
b)y = {x^3} + x + 1\\
c)y = \frac{{x + 1}}{{x + 2}}\\
d)y =  – 3{x^2} – 1\\
e)y = \sqrt {5 – 2x} 
\end{array}\)

1.2. Đồ thị hàm số bậc hai

+)  Đồ thị  hàm số bậc hai \(y = f(x) = a{x^2} + bx + c\) \((a \ne 0)\) là một  parabol  (P):

– Đỉnh \(S\left( { – \frac{b}{{2a}}; – \frac{\Delta }{{4a}}} \right)\)

– Trục đối xứng: đường thẳng \(x =  – \frac{b}{{2a}}\)

– Bề lõm: quay lên trên nếu \(a > 0\), quay xuống dưới nếu \(a < 0\)

– Cắt Oy tại điểm \((0;c)\)

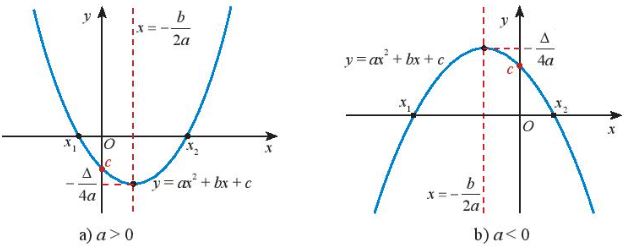
Chú ý:  Nếu PT \(a{x^2} + bx + c = 0\) có hai nghiệm \({x_1},{x_2}\) thì đồ thị hàm số \(y = a{x^2} + bx + c\) cắt trục hoành tại 2 điểm có hoành độ lần lượt là 2 nghiệm này.

+) Vẽ đồ thị

1) Xác định đỉnh \(S\left( { – \frac{b}{{2a}}; – \frac{\Delta }{{4a}}} \right)\)

2) Vẽ trục đối xứng d: \(x =  – \frac{b}{{2a}}\)

3) Tìm tọa độ giao điểm của đồ thị với trục tung (A(0;c)), trục hoành (nếu có).

Xác định \(B\left( {\frac{{ – b}}{a};c} \right)\) (là điểm đối xứng với A qua d)

4) Vẽ parabol đỉnh S, trục đối xứng d, đi qua các điểm tìm được.

1.3. Sự biến thiên của hàm số bậc hai

+) Bảng biến thiên

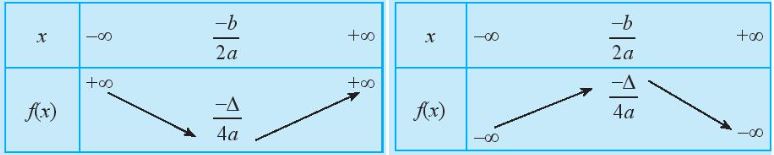
+) Kết luận:

	\(a > 0\)	\(a < 0\)
Trên khoảng \(\left( { – \infty ;\frac{{ – b}}{{2a}}} \right)\)	Hàm số nghịch biến	Hàm số đồng biến
Trên khoảng \(\left( {\frac{{ – b}}{{2a}}; + \infty } \right)\)	Hàm số đồng biến	Hàm số nghịch biến
GTLN hoặc GTNN	Đạt GTNN bằng \(\frac{{ – \Delta }}{{4a}}\) tại \(x = \frac{{ – b}}{{2a}}\)	Đạt GTLN bằng \(\frac{{ – \Delta }}{{4a}}\) tại \(x = \frac{{ – b}}{{2a}}\)
Tập giá trị	\(T = \left[ {\left. {\frac{{ – \Delta }}{{4a}}; + \infty } \right)} \right.\)	\(T = \left( {\left. { – \infty ;\frac{{ – \Delta }}{{4a}}} \right]} \right.\)

Ví dụ: Lập bảng biến thiên của hàm số \(y =  – {x^2} + 4x – 3\). Hàm số này có giá trị lớn nhất hay giá trị nhỏ nhất? Tìm giá trị đó.

Giải

Đỉnh S có tọa độ: \({x_s} = \frac{{ – b}}{{2a}} = \frac{{ – 4}}{{2.\left( { – 1} \right)}} = 2;{y_s} =  – {2^2} + 4.2 – 3 = 1\)

Hay S(2; 1) 

Vì hàm số bậc hai có a = -1 < 0 nên ta có bảng biến thiên sau:

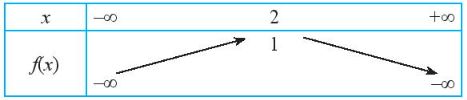
Hàm số đạt giá trị lớn nhất bằng 1 khi x = 2.

1.4. Ứng dụng của hàm số bậc hai

+) Tầm bay cao và tầm bay xa

Chọn điểm \((0;{y_0})\) là điểm xuất phát thì phương trình quỹ đạo của cầu lông khi rời mặt vợt là:

\(y = \frac{{ – g.{x^2}}}{{2.{v_0}^2.{{\cos }^2}\alpha }} + \tan \alpha .x + {y_0}\)

Trong đó:

\(g\) là giá tốc trọng trường ( \( \approx 9,8\;m/{s^2}\))

\(\alpha \) là góc phát cầu (so với phương ngang của mặt đất)

\({v_0}\) là vận tốc ban đầu của cầu

\({y_0}\) là khoảng cách từ vị trí phát cầu đến mặt đất

Quỹ đạo chuyển động của cầu lông là một parabol.

 

 – Vị trí cao nhất tại đỉnh parabol, gọi là  tầm bay cao ;

– Khoảng cách từ nơi đứng phát cầu đến điểm cham đất, gọi là  tầm bay xa .

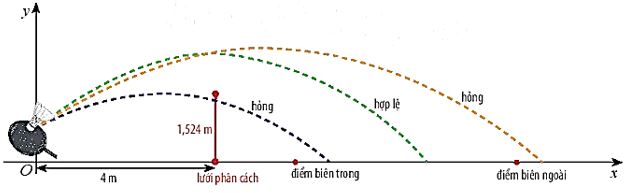
+) Bài toán ứng dụng

Khi cầu bay tới vị trí lưới phân cách, nếu nó ở bên trên mặt lưới và điểm rơi không ra khỏi đường biến phía sân đối phương thì lần phát cầu được xem là hợp lệ.

Câu 1:  Khai triển biểu thức của các hàm số sau và sắp xếp theo thứ tự lũy thừa của x giảm dần (nếu có thể). Hàm số nào có lũy thừa bậc cao nhất của x là bậc hai?

a) \(y = 2x(x – 3)\)

b) \(y = x({x^2} + 2) – 5\)

c) \(y =  – 5(x + 1)(x – 4)\)

Hướng dẫn giải

a) \(y = 2x(x – 3) = 2{x^2} – 6\)

Hàm số có lũy thừa bậc cao nhất của x là bậc hai

b) \(y = x({x^2} + 2) – 5 = {x^3} + 2x – 5\)

Hàm số có lũy thừa bậc cao nhất của x là bậc ba

c) \(y =  – 5(x + 1)(x – 4) =  – 5{x^2} + 15x + 20\)

Hàm số có lũy thừa bậc cao nhất của x là bậc hai

Câu 2:  Vẽ đồ thị hàm số \(y = {x^2} – 4x + 3\) 

Hướng dẫn giải

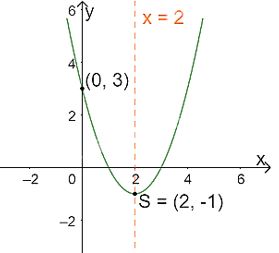
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = f(x) = {x^2} – 4x + 3\) là một parabol (P1):

+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ – b}}{{2a}} = \frac{{ – ( – 4)}}{{2.1}} = 2;{y_S} = {2^2} – 4.2 + 3 =  – 1.\)

+ Có trục đối xứng là đường thẳng \(x = 2\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);

+ Bề lõm quay lên trên vì \(a = 1 > 0\)

+ Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3).

Ta vẽ được đồ thị như hình dưới.

Câu 3:  Tìm khoảng đồng biến, khoảng nghịch biến của hàm số \(y = 2{x^2} – 6x + 11.\) Hàm số này có thể đạt giá trị bằng -1 không? Tại sao?

Hướng dẫn giải

Đỉnh S có tọa độ: \({x_S} = \frac{{ – b}}{{2a}} = \frac{{ – ( – 6)}}{{2.2}} = \frac{3}{2};{y_S} = 2.{\left( {\frac{3}{2}} \right)^2} – 6.\frac{3}{2} + 11 = \frac{{13}}{2}.\)

Hay \(S\left( {\frac{3}{2};\frac{{13}}{2}} \right).\)

Vì hàm số bậc hai có \(a = 2 > 0\) nên ta có bảng biến thiên sau:

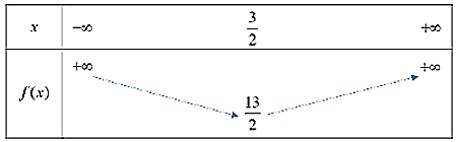
Hàm số đồng biến trên khoảng \((\frac{3}{2}; + \infty )\) và nghịch biến trên khoảng \(( – \infty ;\frac{3}{2})\)

Hàm số đạt giá trị nhỏ nhất bằng \(\frac{{13}}{2}\) khi \(x = \frac{3}{2}\)

Do đó hàm số không thể đạt giá trị bằng -1 vì \( – 1 < \frac{{13}}{2}.\)

===========
Chuyên mục: Chương 3: Hàm số bậc hai và đồ thị