Trả lời câu hỏi trong bài 1 Hàm số và đồ thị – Chân trời

Trả lời câu hỏi trong bài 1 Hàm số và đồ thị – Chân trời
============

KHỞI ĐỘNG

Nhiệt độ có mối liên hệ gì với thời gian?

Hướng dẫn giải:

Thời gian thay đổi thì nhiệt độ thay đổi.

1. HÀM SỐ. TẬP XÁC ĐỊNH VÀ TẬP GIÁ TRỊ CỦA HÀM SỐ

Khám phá 1:  Bản tin dự báo thời tiết cho biết nhiệt độ ở một số thời điểm trong ngày 1/5/2021 tại Thành phố Hồ Chí Minh đã được ghi lại thành bảng kèm với biểu đồ bên:

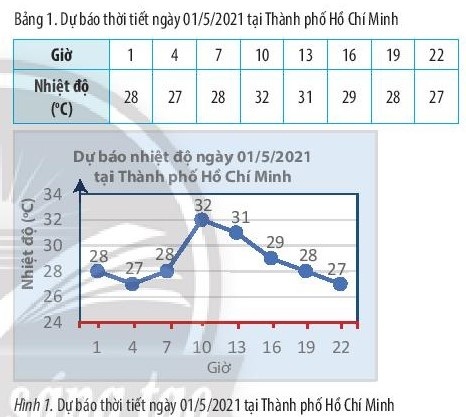
Sử dụng bảng hoặc biểu đồ, hãy:

a. Viết tập hợp các mốc giờ đã có dự báo nhiệt độ.

b. Viết tập hợp các số đo nhiệt độ đã dự báo.

c. Cho biết nhiệt độ dự báo tại Thành phố Hồ Chí Minh vào lúc 7 giờ sáng ngày 1/5/2021.

Hướng dẫn giải:

a. A = {1; 4; 7; 10; 13; 16; 19; 22}

b. B = {28; 27; 28; 32; 31; 29; 28; 27}

c. Nhiệt độ dự báo tại TP. HCM lúc 7 giờ sáng ngày 1/5/2021 là $28^{\circ}$.

Thực hành 1:  Một thiết bị đã ghi lại vận tốc v (mét/giây) ở thời điểm t (giây) của một vật chuyển động như trong bảng sau:

Vì sao bảng này biểu thị một số hàm số? Tìm tập xác định của hàm số này.

Hướng dẫn giải:

Ta thấy ứng với mỗi thời điểm t(giây) trong bảng đều có một giá trị vận tốc v(mét/giây). Vì vậy, bảng này biểu thị một hàm số.

Hàm số đó có tập xác định D = {0,5; 1; 1,2; 1,8; 2,5}.

Thực hành 2:  Tìm tập xác định của các hàm số sau:

a. f(x) = $\sqrt{2x + 7}$                       b. f(x) = $\frac{x + 4}{x^{2} – 3x + 2}$

Hướng dẫn giải:

a. Biểu thức f(x) có nghĩa khi và chỉ khi 2x + 7 $\geq$ 0 <=> x $\geq$ $\frac{-7}{2}$

Vậy tập xác định của hàm số này là D = [$\frac{-7}{2}$; +$\infty$)

b. Biểu thức f(x) có nghĩa khi và chỉ khi x^{2} – 3x + 2 $\neq$ 0 <=> (x – 1)(x – 2) $\neq$ 0 <=> x $\neq$ 1 và x $\neq$ 2.

Vậy tập xác định của hàm số này là D = $\mathbb{R}$\{1; 2}

Vận dụng:  Ở góc của miếng đất hình chữ nhật, người ta làm một bồn hoa có dạng một phần tư hình tròn với bán kính r (Hình 2). Bán kính bồn hoa có kích thước từ 0,5m đến 3m.

a. Viết công thức của hàm số biểu thị diện tích bồn hoa theo bán kính r và tìm tập xác định của hàm số này.

b. Bán kính của bồn hoa bằng bao nhiêu thì nó có diện tích là 0,5$\pi m^{2}$?

Hướng dẫn giải:

a. Công thức: $\frac{1}{4}\pi r^{2}$. 

Tập xác định của hàm số là: D = [0,5; 3]

b. S = 0,5$\pi$ <=> $\frac{1}{4}\pi r^{2}$ = 0,5$\pi$ <=> $r^{2}$ = 2 <=> r = $\sqrt{2}$ (vì r $\in [0,5; 3]$)

2. ĐỒ THỊ HÀM SỐ

Khám phá 2:  Xét hàm số y = f(x) cho bởi bảng sau:

a. Tìm tập xác định D của hàm số trên.

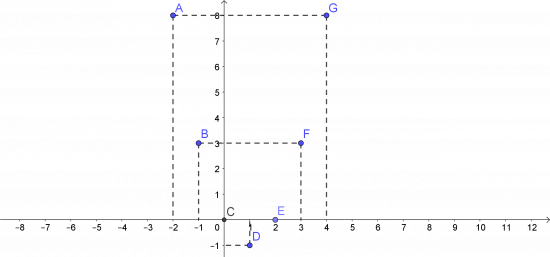
b. Trong mặt phẳng tọa độ Oxy, vẽ tất cả các điểm có tọa độ (x; y) với x $\in$ D và y = f(x).

Hướng dẫn giải:

a. Tập xác định của hàm số là D = {-2; -1; 0; 1; 2; 3; 4}

b. 

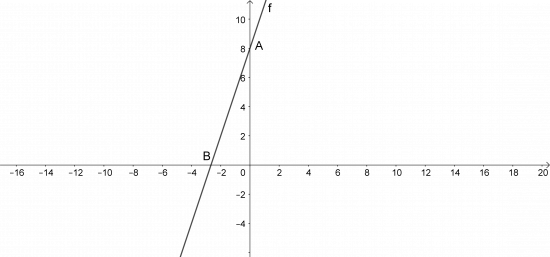
Thực hành 3:  Vẽ đồ thị hàm số f(x) = 3x + 8

Hướng dẫn giải:

Với x = 0 => f(0) = 8. Ta có điểm A(0; 8)

Với x = $\frac{-8}{3}$ => f($\frac{-8}{3}$) = 0. Ta có điểm B($\frac{-8}{3}$; 0)

Vẽ đường thẳng f đi qua hai điểm A và B, ta có f là đồ thị của hàm số f(x) = 3x + 8.

3. HÀM SỐ ĐỒNG BIẾN, HÀM SỐ NGHỊCH BIẾN

Thực hành 4:

a) Tìm khoảng đồng biến và nghịch biến của hàm số có đồ thị sau:

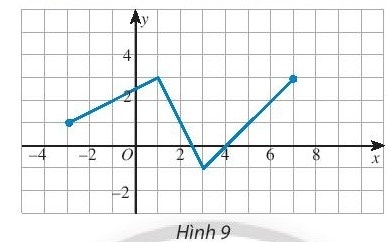
b. Xét tính đồng biến, nghịch biến của hàm số y = f(x) = 5$x^{2}$ trên khoảng (2; 5)

Hướng dẫn giải:

a. Từ đồ thị, ta thấy hàm số xác định trên [-3; 7]

• Trên khoảng (-3; 1), đồ thị có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (-3; 1).
• Trên khoảng (1; 3), đồ thị có dạng đi xuống từ trái sang phải nên hàm số này nghịch biến trên khoảng (1; 3).
• Trên khoảng (3; 7), đồ thị có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (3; 7).

b. Xét hàm số y = f(x) = 5$x^{2}$ trên khoảng (2;5)

Lấy $x_{1}$, $x_{2}$ tùy ý sao cho $x_{1}$ < $x_{2}$, ta có: f($x_{1}$) – f($x_{2}$) = 5($x_{1}^{2}$ – $x_{2}^{2}$) = 5($x_{1}$ + $x_{2}$)($x_{1}$ – $x_{2}$) 

Do $x_{1}$ < $x_{2}$ nên $x_{1}$ – $x_{2}$ < 0 và do $x_{1}$, $x_{2}$ $\in$ (2; 5) nên ($x_{1}$ + $x_{2}$) > 0. Từ đây suy ra f($x_{1}$) – f($x_{2}$) < 0 hay f($x_{1}$) < f($x_{2}$).

Vậy hàm số đồng biến (tăng) trên khoảng (2; 5).

===========
Chuyên mục: Học Toán lớp 10 – Chân trời