Lý thuyết Bài 1: Tọa độ của vectơ – Chân trời
============
1.1. Toạ độ của vectơ đối với một hệ trục toạ độ
Mặt phẳng mà trên đó đã cho một hệ trục toạ độ Oxy được gọi là mặt phẳng toa độ Oxy, hay gọi tắt là mặt phẳng Oxy.
*Toạ độ của một vectơ
| Trong mặt phẳng Oxy, cặp số (x; y) trong biêu diễn \(\overrightarrow a = x\overrightarrow i + y\overrightarrow j \) được gọi là toạ độ của vectơ \(\overrightarrow a \). kí hiệu \(\overrightarrow a \) = (x, y), x gọi là hoành độ, y gọi là tung độ của vectơ \(\overrightarrow a \). |
|---|
Chú ý:
+ \(\overrightarrow a = \left( {x,y} \right) \Leftrightarrow \overrightarrow a = x\overrightarrow i + y\overrightarrow j \)
+ Nếu cho \(\overrightarrow a = \left( {x,y} \right)\) và \(\overrightarrow b = \left( {x’,y’} \right)\) thì \(\overrightarrow a = \overrightarrow b \Leftrightarrow \left\{ \begin{array}{l}
x = x’\\
y = y’
\end{array} \right.\)
*Toạ độ của một điểm
| Trong mặt phẳng toa độ, cho một điểm M tuỳ ý. Toạ độ của vectơ \(\overrightarrow {OM} \) được gọi là toạ độ của điểm M. |
|---|
Nhận xét:
+ Nếu \(\overrightarrow {OM} = \left( {x;y} \right)\) thì cặp số (x; y) là toa độ của điểm M, kí hiệu M(x; y), x gọi là hoành độ, y gọi là tung độ của điểm M
+ \(M\left( {x;y} \right) \Leftrightarrow \overrightarrow {OM} = x\overrightarrow i + y\overrightarrow j \)
Chú ý: Hoành độ của điểm M còn được kí hiệu là xM, tung độ của điểm M còn được kí hiệu là yM. Khi đó ta việt M(xM; yM).
Ví dụ:
Trong mặt phẳng Oxy, cho ba điểm A, B, C được biểu điễn như Hình sau.
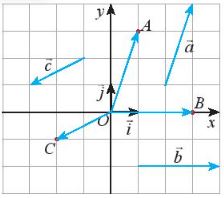
a) Hãy biểu thị các vectơ \(\overrightarrow {OA} ,\overrightarrow {OB} ,\overrightarrow {OC} \) qua hai vectơ \(\overrightarrow i\) và \(\overrightarrow j \) .
b) Tìm toa độ của các vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) và các điểm A, B, C.
Giải
a) Ta có: \(\overrightarrow {OA} = \overrightarrow i + 3\overrightarrow j ,\overrightarrow {OB} = 3\overrightarrow i + 0\overrightarrow j ,\overrightarrow {OC} = – 2\overrightarrow i – \overrightarrow j \)
b) Từ kết quả trên, suy ra: \(\overrightarrow a = \overrightarrow {OA} = (1;3),\overrightarrow b = \overrightarrow {OB} = (3;0),\overrightarrow c = \overrightarrow {OC} = ( – 2; – 1)\)
Do đó A(1; 3), B(3: 0), C(-2; -1)
1.2. Biểu thức toạ độ của các phép toán vectơ
|
Cho hai vectơ \(\overrightarrow a = \left( {{a_1};{a_2}} \right),\overrightarrow b = \left( {{b_1};{b_2}} \right)\) và số thưucj k. Khi đó: \(\begin{array}{l} |
|---|
Ví dụ: Cho hai vectơ \(\overrightarrow a = \left( {1;5} \right),\overrightarrow b = \left( {4; – 2} \right)\). Tìm toạ độ của các vectơ \(\overrightarrow a + \overrightarrow b ,\overrightarrow a – \overrightarrow b ,3\overrightarrow a , – 5\overrightarrow b \)
Giải
\(\begin{array}{l}
\overrightarrow a + \overrightarrow b = \left( {1 + 4;5 + \left( { – 2} \right)} \right) = \left( {5;3} \right);\\
\overrightarrow a – \overrightarrow b = \left( {1 – 4;5 – \left( { – 2} \right)} \right) = \left( { – 3;7} \right);\\
3\overrightarrow a = \left( {3.1;3.5} \right) = \left( {3;15} \right);\\
– 5.\overrightarrow b = \left( { – 5.4; – 5.\left( { – 2} \right)} \right) = \left( { – 20;10} \right)
\end{array}\)
1.3. Áp dụng của toạ độ vectơ
* Liên hệ giữa toạ độ của điểm và toạ độ của vectơ trong mặt phẳng
Cho hai điểm \(A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right)\). Ta có:
\(\overrightarrow {AB} = \left( {{x_B} – {x_A};{y_B} – {y_A}} \right)\)
* Toạ độ trung điểm của đoạn thẳng và trọng tâm của tam giác
Cho hai điểm \(A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right)\). Toa độ trung điểm \(M\left( {{x_M};{y_M}} \right)\) của đoạn thẳng AB là
\({x_M} = \frac{{{x_A} + {x_B}}}{2};{y_M} = \frac{{{y_A} + {y_B}}}{2}\)
Cho tam giác ABC có \(A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right),C\left( {{x_C};{y_C}} \right)\). Toa độ trọng tâm \(G\left( {{x_G};{y_G}} \right)\) của tam giác ABC là:
\({x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3};{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3}\)
Ví dụ
Cho tam giác MNP có toạ độ các đỉnh là M(2; 2), N(6; 3) và P(5; 5)
a) Tìm toa đô trung điểm E của cạnh MN.
b) Tìm toa độ trọng tâm G của tam giác MNP.
Giải
Ta có: \({x_E} = \frac{{{x_M} + {x_N}}}{2} = \frac{{2 + 6}}{2} = 4;{y_E} = \frac{{{y_M} + {y_N}}}{2} = \frac{{2 + 3}}{2} = \frac{5}{2}\). Vậy \(E\left( {4;\frac{5}{2}} \right)\)
Ta có: \({x_G} = \frac{{{x_M} + {x_N} + {x_P}}}{3} = \frac{{2 + 6 + 5}}{3} = \frac{{13}}{3};{y_G} = \frac{{{y_M} + {y_N} + {y_P}}}{3} = \frac{{2 + 3 + 5}}{3} = \frac{{10}}{3}\)
Vậy \(G\left( {\frac{{13}}{3};\frac{{10}}{3}} \right)\)
Câu 1: Trong mặt phẳng Oxy, cho điểm M. Xác định tọa độ của vectơ \(\overrightarrow {OM} \)
Hướng dẫn giải
Cho điểm M(x;y) bất kì, xác định \({M_1},{M_2}\) lần lượt là hình chiếu vuông góc của M xuống trục hoành và trục tung
Dễ thấy \(\overrightarrow {O{M_1}}= x\overrightarrow i ; \, \overrightarrow {O{M_2}} = y \overrightarrow j \)
Áp dụng quy tắc hình bình hành ta có \(\overrightarrow {OM} = \overrightarrow {O{M_1}} + \overrightarrow {O{M_2}} = x\overrightarrow i + y\overrightarrow j \)
Vậy tọa độ của vectơ \(\overrightarrow {OM} \) là (x;y), trùng với tọa độ điểm M.
Câu 2: Cho hai vectơ \(\overrightarrow m = \left( { – 6;1} \right),\overrightarrow n = \left( {0;2} \right)\)
a) Tìm tọa độ các vectơ \(\overrightarrow m + \overrightarrow n ,\overrightarrow m – \overrightarrow n ,10\overrightarrow m , – 4\overrightarrow n \)
b) Tính các tích vô hướng \(\overrightarrow m .\overrightarrow n ,\left( {10\overrightarrow m } \right).\left( { – 4\overrightarrow n } \right)\)
Hướng dẫn giải
a) Ta có
\(\begin{array}{l}\overrightarrow m + \overrightarrow n = \left( {\left( { – 6 + 0} \right);1 + 2} \right) = ( – 6;3)\\\overrightarrow m – \overrightarrow n = \left( {\left( { – 6 – 0} \right);\left( {1 – 2} \right)} \right) = \left( { – 6; – 1} \right)\\10\overrightarrow m = (10.( – 6);10.1) = ( – 60;10)\\ – 4\overrightarrow n = (( – 4).0;( – 4).2) = (0; – 8)\end{array}\)
b) Ta có
\(\overrightarrow m .\overrightarrow n = ( – 6).0 + 1.2 = 0 + 2 = 2\)
Ta có \(10\overrightarrow m = ( – 60;10)\) và \( – 4\overrightarrow n = (0; – 8)\) nên \(\left( {10\overrightarrow m } \right).\left( { – 4\overrightarrow n } \right) = ( – 60).0 + 10.( – 8) = 0 – 80 = – 80\)
===========
Chuyên mục: Chương 9: Phương pháp tọa độ trong mặt phẳng
