Trả lời câu hỏi trong bài 3 Đường tròn trong mặt phẳng tọa độ – Chân trời
============
KHỞI ĐỘNG
Một nông trại tưới nước theo phương pháp vòi phun xoay vòng trung tâm. Cho biết tâm một vòi phun được đặt tại tọa độ (30; 40) và vòi có thể phun xa tối đa 50m. Làm thế nào để viết phương trình biểu diễn tập hợp các điểm xa nhất mà vòi này có thể phun tới?

Hướng dẫn giải:
Phương trình biểu diễn tập hợp các điểm xa nhất mà vòi có thể phun tới là phương trình đường tròn tâm I(30; 40), bán kính R = 50:
$(x – 30)^{2} + (y – 40)^{2} = 50^{2}$
1. PHƯƠNG TRÌNH ĐƯỜNG TRÒN
Khám phá 1: Hãy nhắc lại công thức tính khoảng cách giữa hai điểm I(a; b) và M(x; y) trong mặt phẳng Oxy.
Hướng dẫn giải:
IM = $\sqrt{(x – a)^{2} + (y – b)^{2}}$
Thực hành 1: Viết phương trình đường tròn (C) trong các trường hợp sau:
a. (C) có tâm O(0; 0), bán kính R = 4;
b. (C) có tâm I(2; – 2), bán kính R = 8;
c. (C) đi qua ba điểm A(1; 4), B(0; 1), C(4; 3).
Hướng dẫn giải:
a. Phương trình đường tròn (C) có tâm O(0; 0), bán kính R = 4 là: $x^{2} + y^{2} = 16$
b. Phương trình đường tròn (C) có tâm I(2; – 2), bán kính R = 8 là: $(x – 2)^{2} + (y + 2)^{2} = 64$
c. Gọi I(a; b) là tâm đường tròn (C). Phương trình đường tròn C có dạng:
$x^{2} + y^{2} – 2ax – 2by + c = 0$
(C) đi qua ba điểm A(1; 4), B(0; 1), C(4; 3) nên ta có hệ phương trình:
$\left\{\begin{matrix}1^{2} + 4^{2} – 2a – 8b + c = 0\\ 0^{2} + 1^{2} – 2b + c = 0\\ 4^{2} + 3^{2} – 8a – 6b + c = 0\end{matrix}\right.$ $\Leftrightarrow$ $\left\{\begin{matrix}2a + 8b – c = 17\\2b – c = 1\\ 8a + 6b – c = 25\end{matrix}\right.$ $\Leftrightarrow$ $\left\{\begin{matrix}a = 2\\ b = 2\\ c = 3\end{matrix}\right.$
Vậy phương trình đường tròn (C) là: $x^{2} + y^{2} – 4x – 4y + 3 = 0$
Thực hành 2: Phương trình nào sao đây là phương trình đường tròn? Tìm tọa độ tâm và bán kính của đường tròn đó.
a. $x^{2} + y^{2} – 2x – 4y – 20 = 0$; b. $(x + 5)^{2} + (y + 1)^{2} = 121$
c. $x^{2} + y^{2} – 4x – 8y + 5 = 0$; d. $2x^{2} + 2y^{2} + 6x + 8y – 2 = 0$
Hướng dẫn giải:
a. Phương trình đã cho có dạng: $x^{2} + y^{2} – 2ax – 2by + c = 0$ với a = 1; b = 2; c = -20.
Ta có: $a^{2} + b^{2} – c$ = $1^{2} + 2^{2} + 20 = 25 > 0$. Vậy đây là phương trình đường tròn có tâm I(1; 2) và bán kính R = $\sqrt{25}$ = 5.
b. Phương trình có dạng $(x – a)^{2} + (y – b)^{2} = R^{2}$ với a = -5; b = -1; R = 11.
Vậy đây là phương trình đường tròn có tâm I(-5; -1) và bán kính R = 11.
c. Phương trình có dạng $x^{2} + y^{2} – 2ax – 2by + c = 0$ với a = 2; b = 4; c = 5.
Ta có: $a^{2} + b^{2} – c$ = $2^{2} + 4^{2} – 5 = 15 > 0$. Vậy đây là phương trình đường tròn có tâm I(2; 4) và bán kính R = $\sqrt{15}$.
d. Ta có: $2x^{2} + 2y^{2} + 6x + 8y – 2 = 0$ $\Leftrightarrow$ $x^{2} + y^{2} + 3x + 4y – 1 = 0$
Phương trình có dạng $x^{2} + y^{2} – 2ax – 2by + c = 0$ với a = $-\frac{3}{2}$; b = -2; c = -1.
Ta có: $a^{2} + b^{2}$ – c = $(\frac{-3}{2})^{2} + (-2)^{2}$ + 1 = $\frac{29}{4}$ > 0. Vậy đây là phương trình đường tròn có tâm I($\frac{-3}{2}$; -2) và bán kính R = $\frac{\sqrt{29}}{2}$.
Vận dụng 1: Theo dữ kiện đã cho trong hoạt động khởi động của bài học, viết phương trình đường tròn biểu diễn tập hợp các điểm xa nhất mà vòi nước có thể phun tới.
Hướng dẫn giải:
Phương trình biểu diễn tập hợp các điểm xa nhất mà vòi có thể phun tới là phương trình đường tròn tâm I(30; 40), bán kính R = 50:
$(x – 30)^{2} + (y – 40)^{2} = 50^{2}$
Vận dụng 2: Một sân khấu đã được thiết lập một hệ trục tọa độ để đạo diễn có thể sắp đặt ánh sáng và xác định vị trí của các diễn viên. Cho biết một đèn chiếu sáng đang rọi trên sân khấu một vùng sáng bên trong đường tròn (C) có phương trình $(x – 13)^{2} + (y – 4)^{2} = 16.
a. Tìm tọa độ tâm và bán kính của đường tròn (C).
b. Cho biết tọa độ trên sân khấu của ba diễn viên như sau: A(11; 4), B(8; 5), C(15; 5). Diễn viên nào đang được đèn chiếu sáng?
Hướng dẫn giải:
a. Đường tròn (C) có tâm I(13; 4) và bán kính R = $\sqrt{16}$ = 4.
b. Thay tọa độ điểm A(11; 4) vào phương trình đường tròn (C), ta được: $(11 – 13)^{2} + (4 – 4)^{2} = 4 < 16$ $\Rightarrow$ Diễn viên A được chiếu sáng.
Thay tọa độ điểm B(8; 5) vào phương trình đường tròn (C), ta được: $(8 – 13)^{2} + (5 – 4)^{2} = 26 > 16$ $\Rightarrow$ Diễn viên B không được chiếu sáng.
Thay tọa độ điểm C(15; 5) vào phương trình đường tròn (C), ta được: $(15 – 13)^{2} + (5 – 4)^{2} = 5 < 16$ $\Rightarrow$ Diễn viên C được chiếu sáng.
2. PHƯƠNG TRÌNH TIẾP TUYẾN CỦA ĐƯỜNG TRÒN
Khám phá 2: Cho điểm $M_{0}(x_{0}; y_{0})$ nằm trên đường tròn (C) tâm I(a; b) và cho điểm M(x; y) tùy ý trong mặt phẳng Oxy. Gọi $\Delta$ là tiếp tuyến với (C) tại $M_{0}$.
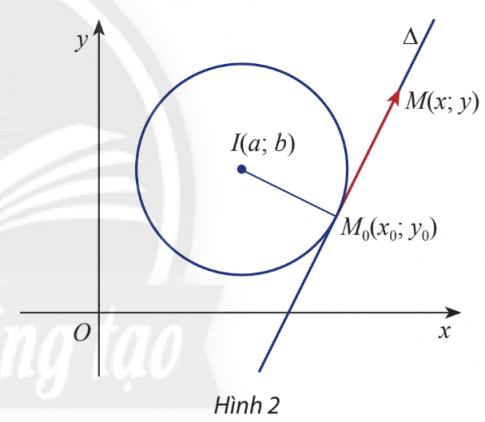
a. Viết tọa độ của hai vectơ $\vec{M_{0}M}$ và $\vec{M_{0}I}$.
b. Viết biểu thức tọa độ tích vô hướng của hai vectơ $\vec{M_{0}M}$ và $\vec{M_{0}I}$.
c. Phương trình $\vec{M_{0}M}.\vec{M_{0}I} = 0$ là phương trình của đường thẳng nào?
Hướng dẫn giải:
a. $\vec{M_{0}M}$ = (x – $x_{0}$; y – $y_{0}$); $\vec{M_{0}I}$ = (a – $x_{0}$; b – $y_{0}$)
b. $\vec{M_{0}M}$. $\vec{M_{0}I}$ = (x – $x_{0}$). (a – $x_{0}$) + (y – $y_{0}$). (b – $y_{0}$) = 0
c. Phương trình $\vec{M_{0}M}.\vec{M_{0}I}$ = 0 là phương trình của đường thẳng $\Delta$.
Thực hành 3: Viết phương trình tiếp tuyến của đường tròn (C): $x^{2} + y^{2}$ – 2x – 4y – 20 = 0 tại điểm A(4; 6).
Hướng dẫn giải:
Ta có: $4^{2} + 6^{2} – 2. 4 – 4. 6 – 20 = 0$ nên A(4; 6) $\in$ (C).
Đường tròn (C) có tâm I(1; 2).
Phương trình tiếp tuyến của (C) tại A(4; 6) là:
$(1 – 4)(x – 4) + (2 – 6)(y – 6) = 0$ $\Leftrightarrow$ $-3x – 4y + 30 = 0$ $\Leftrightarrow$ $3x + 4y – 30 = 0$
Vận dụng 3: Một vận động viên ném đĩa đã vung đĩa theo một đường tròn (C) có phương trình:
$(x – 1)^{2}$ + $(y – 1)^{2}$ = $\frac{169}{144}$
Khi người đó vung đĩa đến vị trí điểm M($\frac{17}{12}$; 2) thì buông đĩa (Hình 4). Viết phương trình tiếp tuyến của đường tròn (C) tại điểm M.
Hướng dẫn giải:
Đường tròn (C) có tâm I(1; 1).
Ta có: $(\frac{17}{12} – 1)^{2} + (2 – 1)^{2}$ = $\frac{169}{144}$ nên M($\frac{17}{12}$; 2) $\in$ (C).
Phương trình tiếp tuyến của đường tròn (C) tại điểm M là:
$(1 – \frac{17}{12})( x – \frac{17}{12}) + (1 – 2)(y – 2) = 0$ $\Leftrightarrow$ $\frac{5}{12}x + y – \frac{373}{144} = 0$
===========
Chuyên mục: Học Toán lớp 10 – Chân trời
