Học Toán lớp 11 – SGK Chân trời

Học Bài 1. Dãy số – Toán 11 CTST Lý thuyết Dãy số – SGK Toán 11 CTST 1. Định nghĩa dãy số – Hàm số u xác định trên tập các số nguyên dương \({\mathbb{N}^*}\)được gọi là một dãy số vô hạn (gọi tắt là dãy số), nghĩa là \(u:{\mathbb{N}^*} \to \mathbb{R}\) \(n \mapsto {u_n} = u\left( n \right)\) Dãy số trên được kí hiệu là \(\left( {{u_n}} \right)\). – Dãy số \(\left( … [Đọc thêm...] vềHọc Bài 1. Dãy số – Toán 11 CTST

HỌC Bài 5. Phương trình lượng giác cơ bản - Toán 11 CTST ============== Lý thuyết Phương trình lượng giác cơ bản – SGK Toán 11 CTST 1. Phương trình tương đương – Hai phương trình được gọi là tương đương khi chúng có cùng tập nghiệm. – Nếu phương trình f(x) =0 tương đương với phương trình g(x) =0 thì ta viết \(f(x) = 0 \Leftrightarrow g(x) = 0\) – Các … [Đọc thêm...] vềHỌC Bài 5. Phương trình lượng giác cơ bản – Toán 11 CTST

Học Bài 4. Hàm số lượng giác và đồ thị - Toán 11 CTST ============ Lý thuyết Hàm số lượng giác và đồ thị 1 . Hàm số lượng giác Quy tắc đặt tương ứng mỗi số thực x với số thực sinx được gọi là hàm số sin, kí hiệu y = sinx. Tập xác định của hàm số sin là \(\mathbb{R}\).   Quy tắc đặt tương ứng mỗi số thực x với số thực cosx được gọi … [Đọc thêm...] vềHọc Bài 4. Hàm số lượng giác và đồ thị – Toán 11 CTST

Học Bài 3. Các công thức lượng giác Toán 11 - CTST ============= Lý thuyết Các công thức lượng giác – SGK Toán 11 CTST 1. Công thức cộng \(\begin{array}{l}\sin \left( {a + b} \right) = \sin a\cos b + \cos asinb\\sin\left( {a – b} \right) = \sin a\cos b – \cos asinb\\\cos \left( {a + b} \right) = \cos a\cos b – \sin asinb\\\cos \left( {a – b} \right) = \cos a\cos b … [Đọc thêm...] vềHọc Bài 3. Các công thức lượng giác Toán 11 – CTST

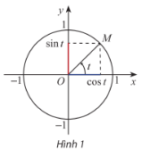
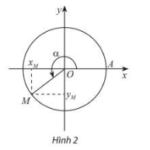
Học Bài 2: Giá trị lượng giác của một góc lượng giác – CTST ============ Lý thuyết Giá trị lượng giác của một góc lượng giác – SGK Toán 11 Chân trời sáng tạo 1. Giá trị lượng giác của góc lượng giác   – Trên đường tròn, lấy điểm M(x;y) như hình vẽ. Khi đó: \(x = \)cos\(\alpha \), \(y = \)sin\(\alpha \). tan\(\alpha \)\( = \frac{{\sin \alpha }}{{\cos … [Đọc thêm...] vềHọc Bài 2: Giá trị lượng giác của một góc lượng giác – CTST

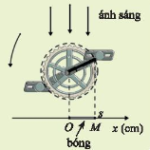
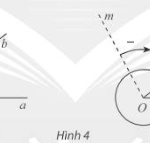
Học Bài 1: Góc lượng giác – CTST ========== Lý thuyết Góc lượng giác – SGK Toán 11 Chân trời sáng tạo 1. Góc lượng giác * Khái niệm góc lượng giác – Cho 2 tia Oa, Ob. Nếu tia Om quay quanh gốc O của nó theo một chiều cố định bắt đầu từ vị trí tia Oa và dừng ở vị trí tia Ob thì ta nói tia Om quét một góc lượng giác có tia đầu Oa, tia cuối Ob. Kí hiệu: (Oa, … [Đọc thêm...] vềHọc Bài 1: Góc lượng giác – CTST