Giải SGK Toán 8 (Cánh Diều) Bài 2: Các phép tính với đa thức nhiều biến

GIẢI CHI TIẾT Giải SGK Toán 8 (Cánh Diều) Bài 2: Các phép tính với đa thức nhiều biến

================
Giải bài tập Toán lớp 8 Bài 2: Các phép tính với đa thức nhiều biến
Giải Toán 8 Trang 11 Tập 1

Bài tập:
Bài 1 trang 16 Toán 8 Tập 1: Thực hiện phép tính:
a) (–xy)(–2x2y + 3xy – 7x);
b)$\left(\frac{1}{6}{x}^2{y}^2\right)(-0,3x^{2}y-0,4xy+1)$;
c) (x + y)(x2+ 2xy + y2);
d) (x – y)(x2– 2xy + y2).
Lời giải:
a) (–xy)(–2x2y + 3xy – 7x)
= (–xy) . (–2x2y) + (–xy) . 3xy – (–xy) . 7x
= 2x3y2– 3x2y2+ 7x2y.
b)$\left(\frac{1}{6}{x}^2{y}^2\right)(-0,3x^{2}y-0,4xy+1)$

c) (x + y)(x2+ 2xy + y2)
= x . x2+ x . 2xy + x . y2+ y . x2+ y . 2xy + y . y2
= x3+ 2x2y + xy2+ x2y + 2xy2+ y3
= x3+ (2x2y + x2y) + (xy2+ 2xy2) + y3
= x3+ 3x2y + 3xy2+ y3.
d) (x – y)(x2– 2xy + y2)
= x . x2– x . 2xy + x . y2– y . x2– y . (– 2xy) – y . y2
= x3– 2x2y + xy2– x2y + 2xy2– y3
= x3– (2x2y + x2y) + (xy2+ 2xy2) – y3
= x3– 3x2y + 3xy2– y3.
Bài 2 trang 16 Toán 8 Tập 1: Thực hiện phép tính:
a) (39x5y7) : (13x2y);
b) $\left(x^2{y}^2+\frac{1}{6}{x}^3{y}^2-x^5{y}^4\right):\left(\frac{1}{2}x{y}^2\right)$.
Lời giải:
a) (39x5y7) : (13x2y) = (39: 13) (x5: x2) (y7: y) = 3x3y6.
b)$\left(x^2{y}^2+\frac{1}{6}{x}^3{y}^2-x^5{y}^4\right):\left(\frac{1}{2}x{y}^2\right)$

Giải Toán 8 trang 17 Tập 1
Bài 3 trang 17 Toán 8 Tập 1: Rút gọn biểu thức:
a) (x – y)(x2+ xy + y2);
b) (x + y)(x2– xy + y2);
c)$(4x-1)(6y+1)-3x\left(8x+\frac{4}{3}\right)$;
d) (x + y)(x – y) + (xy4– x3y2) : (xy2).
Lời giải:
a) (x – y)(x2+ xy + y2)
= x . x2+ x . xy + x . y2– y . x2– y . xy– y . y2
= x3+ (x2y – x2y) + (xy2– xy2) – y3= x3– y3.
b) (x + y)(x2– xy + y2)
= x . x2– x . xy + x . y2+ y . x2– y . xy + y . y2
= x3– x2y + xy2+ x2y – xy2+ y3
= x3+ (x2y – x2y) + (xy2– xy2) + y3
= x3+ y3.
c) (4x – 1)(6y + 1) – 3x$\left(8x+\frac{4}{3}\right)$
= 4x.6y + 4x.1 – 1.6y – 1.1 – 3x.8x – 3x.$\frac{4}{3}$
= 24xy + 4x – 6y – 1 – 24x2– 4x
= 24xy – 24x2+ (4x – 4x) – 6y – 1
= 24xy – 24x2– 6y – 1.
d) (x + y)(x – y) + (xy4– x3y2) : (xy2)
= x . x + x . y – x . y – y . y + (xy4) : (xy2) – (x3y2) : (xy2)
= x2– y2+ y2– x2= (x2– x2) + (y2– y2) = 0.
Bài 4 trang 17 Toán 8 Tập 1: a) Rút gọn rồi tính giá trị của biểu thức.
P = (5x2– 2xy + y2) – (x2+ y2) – (4x2– 5xy + 1)
khi x = 1,2 và x + y = 6,2.
b) Chứng minh giá trị của biểu thức sau không phụ thuộc vào giá trị của biến x:
(x2– 5x + 4)(2x + 3) – (2x2– x – 10)(x – 3).
Lời giải:
a) Ta rút gọn biểu thức P như sau:
P = (5x2– 2xy + y2) – (x2+ y2) – (4x2– 5xy + 1)
= 5x2– 2xy + y2–x2– y2–4x2+ 5xy – 1
= (5x2–x2–4x2)+(5xy – 2xy) + (y2– y2) – 1
= 3xy – 1.
Ta có: x = 1,2; x + y = 6,2 suy ra y = 6,2 – x = 6,2 – 1,2 = 5.
Khi đó, giá trị của biểu thức P khi x = 1,2 và y = 5 là:
3 . 1,2 . 5 – 1 = 18 – 1 = 17.
b) Ta có: (x2– 5x + 4)(2x + 3) – (2x2– x – 10)(x – 3)
= (2x3– 10x2+ 8x + 3x2– 15x + 12) –(2x3– x2– 10x – 6x2+ 3x + 30)
= (2x3– 7x2– 7x+ 12) – (2x3– 7x2– 7x + 30)
= 2x3– 7x2– 7x+ 12–2x3+7x2+ 7x – 30
= (2x3– 2x3) +(7x2– 7x2) +(7x – 7x) + (12– 30) = –8.
Khi đó, với mọi giá trị của biến x thì (x2– 5x + 4)(2x + 3) – (2x2– x – 10)(x – 3) = –8.
Vậy giá trị của biểu thức sau không phụ thuộc vào giá trị của biến x.
Bài 5 trang 17 Toán 8 Tập 1: a) Chứng minh rằng biểu thức P = 5x(2 – x) – (x + 1)(x + 9) luôn nhận giá trị âm với mọi giá trị của biến x.
b) Chứng minh rằng biểu thức Q = 3x2+ x(x – 4y) – 2x(6 – 2y) + 12x + 1 luôn nhận giá trị dương với mọi giá trị của biến x và y.
Lời giải:
a) Ta có: P = 5x(2 – x) – (x + 1)(x + 9)
= (10x – 5x2) – (x2+ x + 9x + 9)
= (10x – 5x2) – (x2+ 10x + 9)
= 10x – 5x2– x2– 10x – 9
= (– 5x2– x2) + (10x – 10x) – 9 = – 9.
Khi đó, với mọi giá trị của biến x thì P = – 9.
Vậy biểu thức P luôn nhận giá trị âm với mọi giá trị của biến x.
b) Ta có: Q = 3x2+ x(x – 4y) – 2x(6 – 2y) + 12x + 1
= 3x2+ x2– 4xy – 12x + 4xy + 12x + 1
= (3x2+ x2) + (4xy – 4xy) + (12x – 12x) + 1
= 4x2+ 1
Vì 4x2≥ 0 nên 4x2+ 1 > 0.
Vậy biểu thức Q luôn nhận giá trị dương với mọi giá trị của biến x và y.
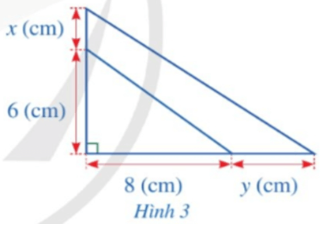
Bài 6 trang 17 Toán 8 Tập 1: Bạn Hạnh dự định cắt một miếng bìa có dạng tam giác vuông với độ dài hai cạnh góc vuông lần lượt là 6 (cm), 8 (cm). Sau khi xem xét lại, bạn Hạnh quyết định tăng độ dài cạnh góc vuông 6 (cm) thêm x (cm) và tăng độ dài cạnh góc vuông 8 (cm) thêm y (cm) (Hình 3). Viết đa thức biểu thị diện tích phần tăng thêm của miếng bìa theo x và y…

Lời giải:
Diện tích tam giác vuông ban đầu là:$\frac{1}{2}$.6.8 = 24 (cm)
Tam giác vuông sau khi mở rộng có độ dài hai cạnh góc vuông lần lượt là x + 6 (cm); y + 8 (cm).
Diện tích tam giác vuông sau khi tăng độ dài hai cạnh góc vuông là:
$\frac{1}{2}$.(x+6).(y+8) =$\frac{1}{2}$xy + 4x + 3y + 24
= 24 + 4x + 3y + 24 = 4x + 3y + 48 (cm)
Vậy đa thức biểu thị diện tích phần tăng thêm của miếng bìa theo x và y là: 4x + 3y + 48 (cm).
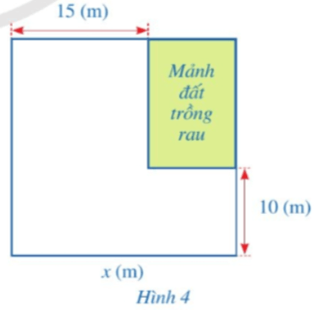
Bài 7 trang 17 Toán 8 Tập 1: Khu vực của nhà bác Xuân có dạng hình vuông. Bác Xuân muốn dành một mảnh đất có dạng hình chữ nhật ở góc khu vườn để trồng rau (Hình 4). Biết diện tích của mảnh đất không trồng rau bằng 475 m2. Tính độ dài x (m) của khu vườn đó.

Lời giải:
Trong Hình 4, ta thấy:
• Khu vực nhà bác Xuân là hình vuông có cạnh x (m)
Diện tích khu vực nhà bác Xuân là: x2(m2).
• Mảnh đất trồng rau có dạng hình chữ nhật có chiều dài bằng x – 10 (m) và chiều rộng bằng x – 15 (m).
Diện tích mảnh đất trồng rau là: (x – 10)(x – 15) = x2– 10x – 15x + 150
= x2– 25x + 150 (m2).
Theo đề bài, diện tích của mảnh đất không trồng rau bằng 475 m2nên ta có:
x2– (x2– 25x + 150) 475
x2– x2+ 25x – 150 = 475
25x – 150 = 475
25x = 625
x = 25.
Vậy khu vườn có độ dài 25 m.

==== ~~~~~~ ====

=============
THUỘC: GIẢI BÀI TẬP SÁCH GIÁO KHOA TOÁN LỚP 8 – CÁNH DIỀU TẬP 1