Ôn tập chương 1 Hình học lớp 10 – Đáp án và lời giải bài 1.48, 1.49, 1.50, 1.51, 1.52, 1.53, 1.54, 1.55, 1.56 trang 45; bài 1.57, 1.58, 1.59, 1.60 trang 46 Sách bài tập (SBT) Toán Hình lớp 10.
Bài 1.48 trang 45
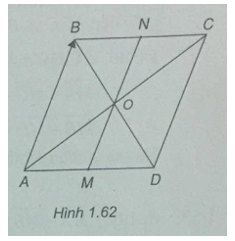
Cho hình bình hành ABCD tâm O. Gọi M và N lần lượt là trung điểm của AD và BC. Dựa vào các điểm A, B, C, D, O, M, N đã cho, hãy:
a) Kể tên hai vec tơ cùng phương với \(\overrightarrow {AB} \), hai vec tơ cùng hướng với \(\overrightarrow {AB} \), hai vec tơ ngược hướng với \(\overrightarrow {AB} \) (các vec tơ kể ra này đều khác \(\overrightarrow 0 \))
b) Chỉ ra một vec tơ bằng vec tơ \(\overrightarrow {MO} \), một vec tơ \(\overrightarrow {OB} \)

a) Hai vec tơ cùng phương với \(\overrightarrow {AB} \) là \(\overrightarrow {MO} ,\overrightarrow {CD} \);
Hai vec tơ cùng hướng với \(\overrightarrow {AB} \) là \(\overrightarrow {ON} ,\overrightarrow {DC} \);
Hai vec tơ ngược hướng với \(\overrightarrow {AB} \) là \(\overrightarrow {OM} ,\overrightarrow {NO} \);
b) Vec tơ \(\overrightarrow {MO} \) là \(\overrightarrow {ON} \)
Vec tơ \(\overrightarrow {OB} \) là \(\overrightarrow {DO} \)
Bài 1.49 trang 45
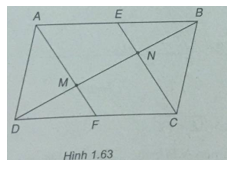
Cho hình bình hành ABCD. Gọi E và F lần lượt là trung điểm của hai cạnh AB và CD. Nối AF và CE, hai đường thẳng này cắt đường chéo BD lần lượt tại M và N. Chứng minh \(\overrightarrow {DM} = \overrightarrow {MN} = \overrightarrow {NB} \)
Gợi ý làm bài
AECF là hình bình hành => EN // AM
E là trung điểm của AB => N là trung điểm của BM, do đó MN = NB.
Tương tự, M là trung điểm của DN, do đó DM = MN.
Vậy \(\overrightarrow {DM} = \overrightarrow {MN} = \overrightarrow {NB} \)
Bài 1.50
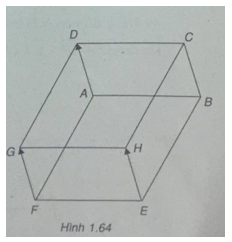
Cho hai hình bình hành ABCD và ABEF với A, D, F không thẳng hàng. Dựng các vec tơ $\(\overrightarrow {EH} \) và \(\overrightarrow {FG} \) bằng vec tơ \(\overrightarrow {AD} \). Chứng minh tứ giác CDGH là hình bình hành.
\(\overrightarrow {EH} = \overrightarrow {AD} ,\overrightarrow {FG} = \overrightarrow {AD} = > \overrightarrow {EH} = \overrightarrow {FG} \)
=>Tứ giác FEHG là hình bình hành
\( = > \overrightarrow {GH} = \overrightarrow {FE} \,(1)\)
Ta có: \(\overrightarrow {DC} = \overrightarrow {AB} ,\overrightarrow {AB} = \overrightarrow {FE} \)
\(\overrightarrow { = > DC} = \overrightarrow {FE} \,(2)\)
Từ (1) và (2) ta có \(\overrightarrow {GH} = \overrightarrow {DC} \)
Vậy tứ giác GHCD là hình bình hành.
Bài 1.51 trang 45 SBT Toán 10
Cho bốn điểm A, B, C, D. Tìm các vec tơ:
a) \(\overrightarrow u = \overrightarrow {AB} + \overrightarrow {DC} + \overrightarrow {BD} + \overrightarrow {CA} \)
b) \(\overrightarrow v = \overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {BC} + \overrightarrow {DA} \)
Giải
a)
\(\eqalign{
& \overrightarrow u = \overrightarrow {AB} + \overrightarrow {DC} + \overrightarrow {BD} + \overrightarrow {CA} \cr
& = (\overrightarrow {AB} + \overrightarrow {BD} ) + (\overrightarrow {DC} + \overrightarrow {CA} ) \cr
& = \overrightarrow {AD} + \overrightarrow {DA} = \overrightarrow {AA} = \overrightarrow 0 \cr} \)
b)
\(\eqalign{
& \overrightarrow v = \overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {BC} + \overrightarrow {DA} \cr
& = (\overrightarrow {DA} + \overrightarrow {AB} ) + (\overrightarrow {BC} + \overrightarrow {CD} ) \cr
& = \overrightarrow {DB} + \overrightarrow {BD} = \overrightarrow {DD} = \overrightarrow 0 \cr} \)
Bài 1.52
Cho lục giác đều ABCDEF và M là một điểm tùy ý. Chứng minh rằng:
\(\overrightarrow {MA} + \overrightarrow {MC} + \overrightarrow {ME} = \overrightarrow {MB} + \overrightarrow {MD} + \overrightarrow {MF} \)
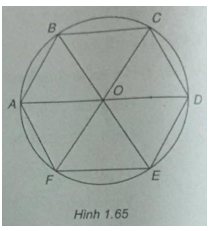
Gọi O là tâm lục giác đều. Khi đó O là trọng tâm của các tam giác đều ACE và BDF.
Do đó, với mọi điểm M ta có:
\(\overrightarrow {MA} + \overrightarrow {MC} + \overrightarrow {ME} = 3\overrightarrow {MO} \)
\(\overrightarrow {MB} + \overrightarrow {MD} + \overrightarrow {MF} = 3\overrightarrow {MO} \)
Vậy ta có đẳng thức cần chứng minh.
Bài 1.53 trang 45
Cho tam giác ABC. Tìm điểm M thỏa mãn điều kiện: \(\overrightarrow {MA} – \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \)
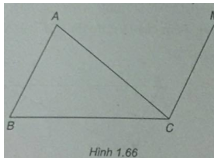
\(\overrightarrow {MA} – \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \Leftrightarrow \overrightarrow {BA} = \overrightarrow {CM} $\)
M là đỉnh của hình bình hành ABCM.
Bài 1.54 trang 45
Cho tam giác ABC có trung tuyến AM. Trên cạnh AC lấy hai điểm E và F sao cho AE = EF = FC. BE cắt trung tuyến AM tại N. Tính \(\overrightarrow {AE} + \overrightarrow {AF} + \overrightarrow {AN} + \overrightarrow {MN} \)
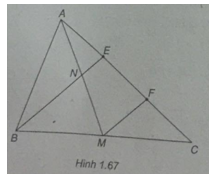
Ta có \(\overrightarrow {AE} = \overrightarrow {FC} \)
Vì MF // BE nên N là trung điểm của AM, suy ra \(\overrightarrow {AN} + \overrightarrow {MN} = \overrightarrow 0 \)
Do đó \(\overrightarrow {AE} + \overrightarrow {AF} + \overrightarrow {AN} + \overrightarrow {MN} = \overrightarrow {AF} + \overrightarrow {FC} = \overrightarrow {AC}\)
Bài 1.55 trang 45 Sách bài tập Toán Hình 10
Cho hai điểm A và B. Điểm M thỏa mãn điều kiện \(\left| {\overrightarrow {MA} + \overrightarrow {MB} } \right| = \left| {\overrightarrow {MA} – \overrightarrow {MB} } \right|\). Chứng minh rằng: \(OM = {1 \over 2}AB\), trong đó O là trung điểm của AB.
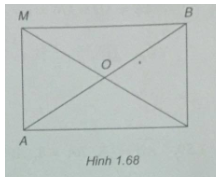
\(\overrightarrow {MA} + \overrightarrow {MB} = 2\overrightarrow {MO} = > \left| {\overrightarrow {MA} + \overrightarrow {MB} } \right| = 2MO\)
\(\overrightarrow {MA} – \overrightarrow {MB} = \overrightarrow {BA} = > \left| {\overrightarrow {MA} – \overrightarrow {MB} } \right| = AB\)
Vậy 2MO = AB hay \(OM = {1 \over 2}AB.\)
Chú ý: Tập hợp các điểm M có tính chất \(\left| {\overrightarrow {MA} + \overrightarrow {MB} } \right| = \left| {\overrightarrow {MA} – \overrightarrow {MB} } \right|\) là đường tròn đường kính AB.
Bài 1.56 SBT Toán hình lớp 10
Cho tam giác ABC và một điểm M tùy ý. Chứng minh rằng vec tơ \(\overrightarrow v = \overrightarrow {MA} + \overrightarrow {MB} – 2\overrightarrow {MC} \) không phụ thuộc vào vị trí của điểm M. Hãy xác định điểm D sao cho \(\overrightarrow {CD} = \overrightarrow v \).
Gợi ý
\(\overrightarrow v = \overrightarrow {MA} + \overrightarrow {MB} – 2\overrightarrow {MC}\)
\( = 2\overrightarrow {ME} – 2\overrightarrow {MC} \) (E là trung điểm cạnh AB)
\( = 2(\overrightarrow {ME} – \overrightarrow {MC} ) = 2\overrightarrow {EC} \)
Vậy \(\overrightarrow v \) không phụ thuộc vị trí của điểm M.
\(\overrightarrow {CD} = \overrightarrow v = 2\overrightarrow {CE} \) thì E là trung điểm của CD. Vậy ta xác định được điểm D.
Bài 1.57 trang 46
Cho tam giác ABC. Gọi M, N , P là những điểm được xác định như sau:
\(\overrightarrow {MB} = 3\overrightarrow {MC} ,\overrightarrow {NC} = 3\overrightarrow {NA} ,\overrightarrow {PA} = 3\overrightarrow {PB} \)
a) Chứng minh \(2\overrightarrow {OM} = 3\overrightarrow {OC} – \overrightarrow {OB} \) với mọi điểm O.
b) Chứng minh hai tam giác ABC và MNP có cùng trọng tâm.
Lời giải
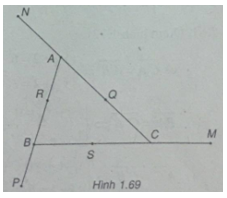
a) $\(3\overrightarrow {OC} – \overrightarrow {OB} = 3(\overrightarrow {OM} + \overrightarrow {MC} ) – (\overrightarrow {OM} + \overrightarrow {MB} )\)
\(= 3(\overrightarrow {OM} – \overrightarrow {OM} ) + (3\overrightarrow {MC} – \overrightarrow {MB} ) = 2\overrightarrow {OM} \)
b) Gọi S, Q và R lần lượt là trung điểm của BC, CA và AB.
\(\overrightarrow {MB} = 3\overrightarrow {MC} = > \overrightarrow {CM} = \overrightarrow {SC} \)
\(\overrightarrow {NC} = 3\overrightarrow {NA} = > \overrightarrow {AN} = \overrightarrow {CQ} \)
\(\overrightarrow {PA} = 3\overrightarrow {PB} = > \overrightarrow {BP} = \overrightarrow {RB} = \overrightarrow {QS} \)
Gọi G là trọng tâm của tam giác ABC thì \(\overrightarrow {GA} + \overrightarrow {BG} + \overrightarrow {GC} = \overrightarrow 0\)
Ta có:
\(\eqalign{
& \overrightarrow {GM} + \overrightarrow {GN} + \overrightarrow {GP} \cr
& = \overrightarrow {GC} + \overrightarrow {CM} + \overrightarrow {GA} + \overrightarrow {AN} + \overrightarrow {GB} + \overrightarrow {BP} \cr} \)
\(\overrightarrow { = (GA} + \overrightarrow {GC} + \overrightarrow {GC} ) + (\overrightarrow {SC} + \overrightarrow {CQ} + \overrightarrow {QS} )\)
\( = \overrightarrow 0 + \overrightarrow 0 \)
Vậy G là trọng tâm của tam giác MNP.
Bài 1.58
Cho hình vuông ABCD, E là trung điểm của CD. Hãy phân tích theo hai vec tơ \(\overrightarrow u = \overrightarrow {AD} ,\overrightarrow v = \overrightarrow {AB} \).
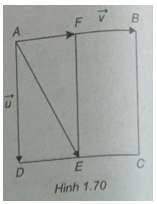
Gọi F là trung điểm của cạnh AB. Ta có
\(\overrightarrow {AE} = \overrightarrow {AD} + \overrightarrow {AF} = \overrightarrow u + {1 \over 2}\overrightarrow v \)
Vậy \(\overrightarrow {AE} = \overrightarrow u + {1 \over 2}\overrightarrow v\)
Bài 1.59
Cho các điểm A, B, C trên trục \((O;\overrightarrow e )\) có tọa độ lần lượt là \(5; – 3; – 4\). Tính độ dài đại số của \(\overrightarrow {AB} ,\overrightarrow {BA} ,\overrightarrow {AC} ,\overrightarrow {BC} \)
Gợi ý làm bài
\(\eqalign{
& \overrightarrow {AB} = – 8,\overrightarrow {BA} = 8, \cr
& \overrightarrow {AC} = – 9,\overrightarrow {BC} = – 1 \cr} \)
Bài 1.60 trang 46 Sách bài tập (SBT) Toán hình 10
Cho hình thoi ABCD tâm O có AC = 8, BD = 6. Chọn hệ tọa độ \((O;\overrightarrow i ,\overrightarrow j )\) sao cho \(\overrightarrow i \) và \(\overrightarrow {OC} \) cùng hướng, \(\overrightarrow j \) và \(\overrightarrow {OB} \) cùng hướng
a) Tìm tọa độ các đỉnh của hình thoi;
b) Tìm tọa độ trung điểm I của BC và trọng tâm của tam giác ABC;
c) Tìm tọa độ điểm đối xứng I’ của I qua tâm O. Chứng minh A, I’, D thẳng hàng
d) Tìm tọa độ của vec tơ \(\overrightarrow {AC} ,\overrightarrow {BD} ,\overrightarrow {BC} \)
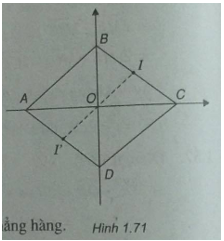
a) Ta có: AO = OC = 4 và OB = OD = 3
\( \Rightarrow A( – 4;0),C(4,0),B(0;3),D(0; – 3)\)
b) I là trung điểm BC \( \Rightarrow I\left( {2;{3 \over 2}} \right)\)
G là trọng tâm tam giác ABC \( \Rightarrow G(0;1)\)
c) I’ đối xứng với I qua O \( \Rightarrow I’\left( { – 2; – {2 \over 3}} \right)\)
Ta có \(\overrightarrow {AI’} \left( {2; – {3 \over 2}} \right),\overrightarrow {AD} \left( {4; – 3} \right)\)
Vậy \(\overrightarrow {AD} = 2\overrightarrow {AI’} \)
Vậy A, I’, D thẳng hàng
d) \(\overrightarrow {AC} (8;0),{\rm{ }}\overrightarrow {BD} (0; – 6),{\rm{ }}\overrightarrow {BC} (4; – 3){\rm{ }}\)
