GIẢI CHI TIẾT Giải SBT Bài 6 Chương 7 – SBT Toán 10 CÁNH DIỀU
===========
Giải bài 59 trang 95 SBT Toán 10 Cánh diều tập 2 – CD
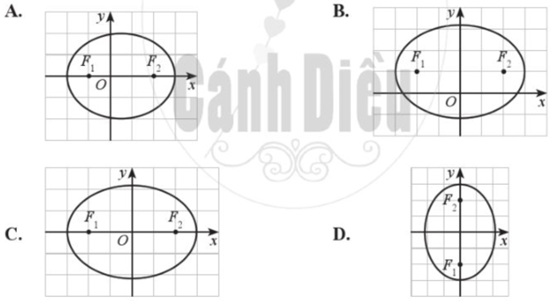
Elip trong hệ trục tọa độ Oxy nào dưới đây có phương trình chính tắc dạng: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) (a > b > 0)?

Phương pháp giải
Đường elip trên hệ trục tọa độ Oxy có 2 tiêu điểm F1, F2 nằm trên trục Ox và đối xứng nhau qua gốc O
Lời giải chi tiết
Hình C là elip có PT chính tắc dạng \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) (a > b > 0)
Chọn C
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 6
Giải bài 60 trang 95 SBT Toán 10 Cánh diều tập 2 – CD
Phương trình nào sau đây là phương trình chính tắc của elip?
A. \(\frac{{{x^2}}}{{{3^2}}} + \frac{{{y^2}}}{{{3^2}}} = 1\)
B. \(\frac{{{x^2}}}{{{3^2}}} – \frac{{{y^2}}}{{{3^2}}} = 1\)
C. \(\frac{{{x^2}}}{6} + {y^2} = 1\)
D. \(\frac{{{x^2}}}{{{2^2}}} + \frac{{{y^2}}}{{{3^2}}} = 1\)
Phương pháp giải
Elip trong hệ trục tọa độ có phương trình chính tắc dạng: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) (a > b > 0)
Lời giải chi tiết
Xét đáp án C ta có: a =\(\sqrt 6 > 1 = b\) thỏa mãn điều kiện nên \(\frac{{{x^2}}}{6} + {y^2} = 1\) là PT elip
Chọn C
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 6
Giải bài 61 trang 96 SBT Toán 10 Cánh diều tập 2 – CD
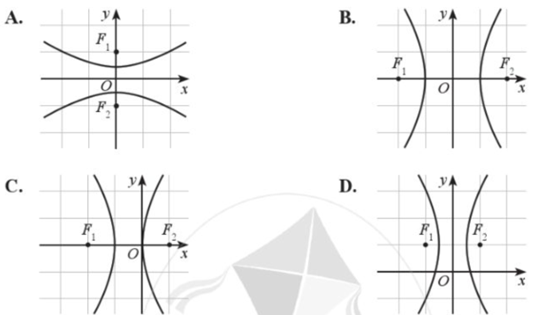
Hypebol trong hệ trục tọa độ Oxy nào dưới đây có phương trình chính tắc dạng: \(\frac{{{x^2}}}{{{a^2}}} – \frac{{{y^2}}}{{{b^2}}} = 1\) (a > 0, b > 0)?
Phương pháp giải
Đường hypebol trên hệ trục tọa độ Oxy có 2 tiêu điểm F1, F2 nằm trên trục Ox và đối xứng nhau qua gốc O
Lời giải chi tiết
Hình B là hypebol trong hệ trục tọa độ Oxy có phương trình chính tắc dạng: \(\frac{{{x^2}}}{{{a^2}}} – \frac{{{y^2}}}{{{b^2}}} = 1\) (a > 0, b > 0)
Chọn B
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 6
Giải bài 62 trang 96 SBT Toán 10 Cánh diều tập 2 – CD
Phương trình nào sau đây là phương trình chính tắc của hypebol?
A. \({x^2} + \frac{{{y^2}}}{{{3^2}}} = 1\)
B. \(\frac{{{x^2}}}{{16}} – {y^2} = – 1\)
C. \(\frac{{{x^2}}}{{25}} – \frac{{{y^2}}}{9} = – 1\)
D. \({x^2} – \frac{{{y^2}}}{2} = 1\)
Phương pháp giải
Hypebol trong hệ trục tọa độ Oxy có phương trình chính tắc dạng: \(\frac{{{x^2}}}{{{a^2}}} – \frac{{{y^2}}}{{{b^2}}} = 1\) (a > 0, b > 0)
Lời giải chi tiết
Xét đáp án D ta có: PT \({x^2} – \frac{{{y^2}}}{2} = 1\) có dạng \(\frac{{{x^2}}}{{{a^2}}} – \frac{{{y^2}}}{{{b^2}}} = 1\) với a = 1, b = \(\sqrt 2 \) nên là PT hypebol
Chọn D
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 6
Giải bài 63 trang 96 SBT Toán 10 Cánh diều tập 2 – CD
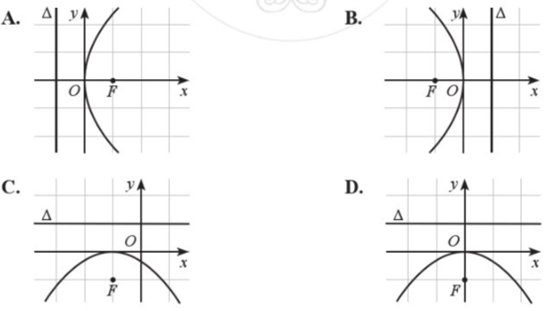
Parabol trong hệ trục tọa độ Oxy nào dưới đây có phương trình chính tắc dạng: \({y^2} = 2px\) (p > 0)?
Phương pháp giải
Đường parabol \({y^2} = 2px\) (p > 0) trong hệ trục tọa độ Oxy có bề lõm quay sang bên phải, đỉnh parabol là gốc O
Lời giải chi tiết
Hình A là parabol trong hệ trục tọa độ Oxy có phương trình chính tắc dạng: \({y^2} = 2px\) (p > 0)
Chọn A
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 6
Giải bài 64 trang 97 SBT Toán 10 Cánh diều tập 2 – CD
Phương trình nào sau đây là phương trình chính tắc của hypebol?
A. \({y^2} = – 0,3x\)
B. \({x^2} = 0,3y\)
C. \({y^2} = 0,3x\)
D. \({x^2} = – 0,3y\)
Phương pháp giải
Parabol trong hệ trục tọa độ Oxy có phương trình chính tắc dạng: \({y^2} = 2px\) (p > 0)
Lời giải chi tiết
Xét đáp án C ta có: PT \({y^2} = 0,3x\) có dạng \({y^2} = 2px\) với \(p = 0,15 > 0\) nên là PT hypebol
Chọn C
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 6
Giải bài 65 trang 97 SBT Toán 10 Cánh diều tập 2 – CD
Lập phương trình chính tắc của elip (E) biết (E) đi qua hai điểm:
\(P\left( {2;\frac{{3\sqrt 3 }}{2}} \right)\) và \(Q\left( {2\sqrt 2 ;\frac{{3\sqrt 2 }}{2}} \right)\)
Phương pháp giải
Bước 1: Thay tọa độ P và Q vào PT chính tắc của Elip để tìm giá trị a và b
Bước 2: Viết PT chính tắc của elip với a và b tìm được ở bước
Lời giải chi tiết
Gọi elip cần lập PT chính tắc là (E). Khi đó (E) có dạng: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) (a > b > 0)
Do \(P\left( {2;\frac{{3\sqrt 3 }}{2}} \right) \in (E)\) nên \(\frac{{{2^2}}}{{{a^2}}} + \frac{{{{\left( {\frac{{3\sqrt 3 }}{2}} \right)}^2}}}{{{b^2}}} = 1 \Leftrightarrow \frac{4}{{{a^2}}} + \frac{{27}}{{4{b^2}}} = 1\)
Do \(Q\left( {2\sqrt 2 ;\frac{{3\sqrt 2 }}{2}} \right) \in (H)\) nên \(\frac{{{{\left( {2\sqrt 2 } \right)}^2}}}{{{a^2}}} + \frac{{{{\left( {\frac{{3\sqrt 2 }}{2}} \right)}^2}}}{{{b^2}}} = 1 \Leftrightarrow \frac{8}{{{a^2}}} + \frac{9}{{2{b^2}}} = 1\)
Ta có hệ PT: \(\left\{ \begin{array}{l}\frac{4}{{{a^2}}} + \frac{{27}}{{4{b^2}}} = 1\\\frac{8}{{{a^2}}} + \frac{9}{{2{b^2}}} = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\frac{1}{{{a^2}}} = \frac{1}{{16}}\\\frac{1}{{{b^2}}} = \frac{1}{9}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{a^2} = 16\\{b^2} = 9\end{array} \right.\)
Vậy elip (E) có PT: \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{9} = 1\)
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 6
Giải bài 66 trang 97 SBT Toán 10 Cánh diều tập 2 – CD
Cho elip (E): \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1\). Tìm điểm P thuộc (E) thoả mãn OP = 2,5.
Phương pháp giải
Bước 1: Tham số hóa tọa độ điểm P và thay tọa độ P vào PT (E)
Bước 2: Lập hệ PT 2 ẩn m2, n2 theo giả thiết
Bước 3: Giải hệ PT tìm tọa độ điểm P
Lời giải chi tiết
Giả sử điểm P có tọa độ P(m ; n)
Do \(P \in (E)\) nên \(\frac{{{m^2}}}{9} + \frac{{{n^2}}}{4} = 1\)
Theo giả thiết, \(OP = 2,5 \Rightarrow O{P^2} = 6,25 \Leftrightarrow {m^2} + {n^2} = 6,25\)
Ta có hệ PT: \(\left\{ \begin{array}{l}{m^2} + {n^2} = 6,25\\\frac{{{m^2}}}{9} + \frac{{{n^2}}}{4} = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{m^2} = \frac{{81}}{{20}}\\{n^2} = \frac{{11}}{5}\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}m = \pm \frac{{9\sqrt 5 }}{{10}}\\n = \pm \frac{{\sqrt {55} }}{5}\end{array} \right.\)
Vậy có 4 điểm P thỏa mãn là: \({P_1}\left( {\frac{{9\sqrt 5 }}{{10}};\frac{{\sqrt {55} }}{5}} \right),{P_2}\left( { – \frac{{9\sqrt 5 }}{{10}};\frac{{\sqrt {55} }}{5}} \right),{P_3}\left( {\frac{{9\sqrt 5 }}{{10}}; – \frac{{\sqrt {55} }}{5}} \right),{P_4}\left( { – \frac{{9\sqrt 5 }}{{10}}; – \frac{{\sqrt {55} }}{5}} \right)\)
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 6
Giải bài 67 trang 97 SBT Toán 10 Cánh diều tập 2 – CD
Lập phương trình chính tắc của hypebol (H), biết (H) đi qua hai điểm M(-1 ; 0) và \(N(2;2\sqrt 3 )\)
Phương pháp giải
Bước 1: Thay tọa độ M và N vào PT chính tắc của Elip để tìm giá trị a và b
Bước 2: Viết PT chính tắc của hypebol với a và b tìm được ở bước 1
Lời giải chi tiết
Gọi hypebol cần lập PT chính tắc là (H). Khi đó (H) có dạng: \(\frac{{{x^2}}}{{{a^2}}} – \frac{{{y^2}}}{{{b^2}}} = 1\) (a > 0, b > 0)
Do \(M\left( { – 1;0} \right) \in (H)\) nên \(\frac{{{{( – 1)}^2}}}{{{a^2}}} = 1 \Leftrightarrow \frac{1}{{{a^2}}} = 1 \Leftrightarrow {a^2} = 1\)
Do \(N\left( {2;2\sqrt 3 } \right) \in (H)\) nên \(\frac{{{2^2}}}{{{a^2}}} – \frac{{{{\left( {2\sqrt 3 } \right)}^2}}}{{{b^2}}} = 1 \Leftrightarrow \frac{4}{1} – \frac{{12}}{{{b^2}}} = 1 \Leftrightarrow {b^2} = 4\)
Vậy hypebol (H) có PT: \(\frac{{{x^2}}}{1} – \frac{{{y^2}}}{4} = 1\)
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 6
Giải bài 68 trang 97 SBT Toán 10 Cánh diều tập 2 – CD
Cho hypebol (H) có phương trình chính tắc: \(\frac{{{x^2}}}{{{a^2}}} – \frac{{{y^2}}}{{{b^2}}} = 1\) với a > 0, b > 0 và đường thẳng y = n cắt (H) tại hai điểm P, Q phân biệt. Chứng minh hai điểm P và Q đối xứng nhau qua trục Oy.
Phương pháp giải
Bước 1: Tham số hóa tọa độ P, Q theo PT đường thẳng y = n
Bước 2: Thay tọa độ P, Q vào PT (H) và chứng minh hoành độ 2 điểm này trái dấu rồi kết luận
Lời giải chi tiết
Do \(P,Q \in d:y = n\) nên \(P(t;n),Q(k;n)\)
Do \(P,Q \in (H)\) nên \(\left\{ \begin{array}{l}\frac{{{t^2}}}{{{a^2}}} – \frac{{{n^2}}}{{{b^2}}} = 1\\\frac{{{k^2}}}{{{a^2}}} – \frac{{{n^2}}}{{{b^2}}} = 1\end{array} \right. \Rightarrow \frac{{{t^2}}}{{{a^2}}} = \frac{{{k^2}}}{{{a^2}}}\)\( \Leftrightarrow {t^2} = {k^2} \Leftrightarrow \left\{ \begin{array}{l}t = k\\t = – k\end{array} \right.\)
Với t = k thì P và Q trùng nhau \( \Rightarrow \) t = k không thỏa mãn
Với t = –k thì P(t ; n) và Q(-t ; n). Khi đó P và Q đối xứng nhau qua trục Oy (ĐPCM)
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 6
Giải bài 69 trang 97 SBT Toán 10 Cánh diều tập 2 – CD
Viết phương trình chính tắc của parabol (P), biết:
a) Phương trình đường chuẩn của (P) là \(x + \frac{1}{8} = 0\)
b) (P) đi qua điểm M(1 ; -8)
Phương pháp giải
Bước 1: Từ PT đường chuẩn của (P) thì giá trị p, thay tọa độ điểm M vào PT chính tắc của (P) để tìm p
Bước 2: Viết PT chính tắc của (P) dạng y2 = 2px (p > 0) với p tìm được ở bước 1
Lời giải chi tiết
PT chính tắc của parabol (P) có dạng y2 = 2px (p > 0)
a) Theo giả thiết, phương trình đường chuẩn của (P) là \(x + \frac{1}{8} = 0\) \( \Rightarrow p = \frac{1}{4}\)
Vậy PT chính tắc của (P) là: \({y^2} = \frac{1}{2}x\)
b) Do \(M(1; – 8) \in (P)\) nên \({( – 8)^2} = 2p.1 \Rightarrow p = 32\)
Vậy PT chính tắc của (P) là: \({y^2} = 64x\)
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 6
Giải bài 70 trang 97 SBT Toán 10 Cánh diều tập 2 – CD
Cho parabol (P) có phương trình chính tắc: y2 = 2px (p > 0) và đường thẳng x = m (m > 0) cắt (P) tại hai điểm I, K phân biệt. Chứng minh hai điểm I và K đối xứng nhau qua trục Ox.
Phương pháp giải
Bước 1: Tham số hóa tọa độ I, K theo PT đường thẳng x = m
Bước 2: Thay tọa độ I, K vào PT (P) và chứng minh tung độ 2 điểm này trái dấu rồi kết luận
Lời giải chi tiết
Do \(I,K \in d:x = m\) nên \(I(m;t),K(m;k)\)
Do \(I,K \in (P)\) nên \(\left\{ \begin{array}{l}{t^2} = 2pm\\{k^2} = 2pm\end{array} \right.\)\( \Leftrightarrow {t^2} = {k^2} \Leftrightarrow \left\{ \begin{array}{l}t = k\\t = – k\end{array} \right.\)
Với t = k thì I và K trùng nhau \( \Rightarrow \) t = k không thỏa mãn
Với t = –k thì I(m ; t) và K(m ; -t). Khi đó I và K đối xứng nhau qua trục Ox (ĐPCM)
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 6
=======
THUỘC: Giải sách bài tập toán 10 – Cánh diều
