GIẢI CHI TIẾT Giải SBT Bài 5 Chương 7 – SBT Toán 10 CÁNH DIỀU
===========
Giải bài 47 trang 88 SBT Toán 10 Cánh diều tập 2 – CD
Phương trình nào sau đây không là phương trình đường tròn?
A. x² + y² = 4
B. x² + y² + 2x – 1 = 0
C. 2x2 + 3y2 + 2x + 3y = 9
D. x² + y² + 4y + 3 = 0
Phương pháp giải
Bước 1: Tìm các PT có hệ số của x2 và y2 khác nhau để tìm ra PT không là PT đường tròn
Bước 2: Nếu các PT đều có hệ số x2 và y2 bằng nhau thì biến đổi các PT còn lại về dạng \({(x – a)^2} + {(y – b)^2} = c\)
Bước 3: Xét dấu của c, nếu c ≤ 0 thì PT đó không là phương trình đường tròn
Lời giải chi tiết
Ta thấy PT 2x2 + 3y2 + 2x + 3y = 9 có hệ số của x2 và y2 khác nhau nên không là phương trình đường tròn
Chọn C
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 5
Giải bài 48 trang 88 SBT Toán 10 Cánh diều tập 2 – CD
Trong mặt phẳng toạ độ Oxy, cho đường tròn (C): (x + 8)2 + (y – 10)2 = 36. Toạ độ tâm I của (C) là:
A. (8; -10)
B. (-8; 10)
C. (-10; 8)
D. (10; -8)
Phương pháp giải
Đường tròn có PT \({(x – a)^2} + {(y – b)^2} = {R^2}\) có tâm I(a ; b)
Lời giải chi tiết
Đường tròn (C): (x + 8)2 + (y – 10)2 = 36 có tâm I(-8 ; 10)
Chọn B
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 5
Giải bài 49 trang 88 SBT Toán 10 Cánh diều tập 2 – CD
Trong mặt phẳng toạ độ Oxy, cho đường tròn (C): (x − 1)2 + (y + 2)2 = 4. Bán kính của (C) bằng:
A. 4
B. 16
C. 2
D. 1
Phương pháp giải
Đường tròn có PT \({(x – a)^2} + {(y – b)^2} = c\) với c > 0 có bán kính \(R = \sqrt c \)
Lời giải chi tiết
Đường tròn (C): (x − 1)2 + (y + 2)2 = 4 có bán kính R = 2
Chọn C
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 5
Giải bài 50 trang 89 SBT Toán 10 Cánh diều tập 2 – CD
Trong mặt phẳng toạ độ Oxy, đường tròn tâm I(− 4 ; 2) bán kính R = 9 có phương trình là:
A. (x – 4)² + (y + 2)² = 81
B. (x + 4)² + (y – 2)² = 9
C. (x – 4)² + (y + 2)² = 9
D. (x + 4)² + (y – 2)² = 81
Phương pháp giải
Đường tròn (C) có tâm I(a ; b), bán kính R có PT dạng chính tắc: (C): \({(x – a)^2} + {(y – b)^2} = {R^2}\)
Lời giải chi tiết
Đường tròn tâm I(− 4 ; 2) bán kính R = 9 có phương trình là: \({(x + 4)^2} + {(y – 2)^2} = 81\)
Chọn D
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 5
Giải bài 51 trang 89 SBT Toán 10 Cánh diều tập 2 – CD
Trong mặt phẳng toạ độ Oxy, cho đường tròn (C): (x − 3)2 + (y − 4)2 = 25. Tiếp tuyến tại điểm M(0; 8) thuộc đường tròn có một vectơ pháp tuyến là:
A. \(\overrightarrow n = ( – 3;4)\)
B. \(\overrightarrow n = (3;4)\)
C. \(\overrightarrow n = (4; – 3)\)
D. \(\overrightarrow n = (4;3)\)
Phương pháp giải
Giả sử d là tiếp tuyến tại M của (C). Khi đó \(IM \bot d\) (I là tâm của (C)) nên d nhận vectơ \(\overrightarrow {OM} \) làm VTPT
Lời giải chi tiết
(C) có tâm I(3; 4), bán kính R = 5
Giả sử d là tiếp tuyến tại M của (C) \( \Rightarrow IM \bot d\) \( \Rightarrow \) d nhận \(\overrightarrow {IM} \) làm VTPT
\( \Rightarrow \)\(\overrightarrow {IM} = ( – 3;4)\)
Chọn A
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 5
Giải bài 52 trang 89 SBT Toán 10 Cánh diều tập 2 – CD
Trong mặt phẳng toạ độ Oxy, cho đường tròn (C): (x – 6)2 + (y – 7)2 = 16. Hai điểm M, N chuyển động trên đường tròn (C). Khoảng cách lớn nhất giữa hai điểm M và N bằng:
A. 16
B. 8
C. 4
D. 256
Phương pháp giải
Khoảng cách lớn nhất giữa hai điểm trên đường tròn là đường kính của đường tròn
Lời giải chi tiết
(C) có tâm I(6 ; 7) và bán kính R = 4.
M, N thuộc đường tròn (C) \( \Rightarrow \) MN đạt GTLN khi MN là đường kính của đường tròn
\( \Rightarrow MN = 8\)
Chọn B
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 5
Giải bài 53 trang 89 SBT Toán 10 Cánh diều tập 2 – CD
Tìm k sao cho phương trình: x2 + y2 – 6x + 2ky + 2k + 12 = 0 là phương trình đường tròn.
Phương pháp giải
Phương trình ax2 + by2 – 2ax – 2by + c = 0 là PT đường tròn khi và chỉ khi giá trị a2 + b2 – c > 0
Lời giải chi tiết
PT x2 + y2 – 6x + 2ky + 2k + 12 = 0 (1) có các giá trị a = 3, b = –k, c = 2k + 12
(1) là PT đường tròn khi và chỉ khi 32 + k2 – 2k – 12 > 0 \( \Leftrightarrow {k^2} – 2k – 3 > 0 \Leftrightarrow \left[ \begin{array}{l}k > 3\\k < – 1\end{array} \right.\)
Vậy với \(k > 3\) hoặc \(k < – 1\) thì PT (1) là phương trình đường tròn
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 5
Giải bài 54 trang 89 SBT Toán 10 Cánh diều tập 2 – CD
Viết phương trình đường tròn (C) trong mỗi trường hợp sau:
a) (C) có tâm I(−6 ; 2) bán kính 7
b) (C) có tâm I(3 ; – 7) và đi qua điểm A(4 ; 1)
c) (C) có tâm I(1 ; 2) và tiếp xúc với đường thẳng 3x + 4y + 19 = 0
d) (C) có đường kính AB với A(−2 ; 3) và B(0 ; 1)
e) (C) có tâm I thuộc đường thẳng \({\Delta _1}:\left\{ \begin{array}{l}x = 1 + t\\y = 1 – t\end{array} \right.\) và (C) tiếp xúc với hai đường thẳng ∆2: 3x + 4y – 1 = 0, ∆3: 3x – 4y + 2 = 0
Phương pháp giải
+) Từ câu a câu d xác định bán kính của (C) rồi viết PT đường tròn dạng chính tắc
+) Xét câu e
Bước 1: Tham số hóa tọa độ tâm I
Bước 2: Lập PT từ giả thiết: \(d(I,{\Delta _2}) = d(I,{\Delta _3})\)
Bước 3: Giải PT tìm được ở bước 2 để tìm tọa độ tâm I và bán kính đường tròn rồi viết PT đường tròn dạng chính tắc
Lời giải chi tiết
a) (C) có tâm I(−6 ; 2) bán kính 7 nên có PT: \({(x + 6)^2} + {(y – 2)^2} = 49\)
b) (C) có tâm I(3 ; – 7) và đi qua điểm A(4 ; 1) \( \Rightarrow \) Bán kính của (C) là \(IA = \sqrt {{{(4 – 3)}^2} + {{(1 + 7)}^2}} = \sqrt {65} \)
\( \Rightarrow \)(C) có PT: \({(x – 3)^2} + {(y + 7)^2} = 65\)
c) (C) có tâm I(1 ; 2) và tiếp xúc với đường thẳng 3x + 4y + 19 = 0
\( \Rightarrow \) Bán kính của (C) là khoảng cách từ tâm I đến đường thẳng ∆: 3x + 4y + 19 = 0
Ta có: \(d(I,\Delta ) = \frac{{\left| {3.1 + 4.2 + 19} \right|}}{{\sqrt {{3^2} + {4^2}} }} = \frac{{30}}{5} = 6\)
\( \Rightarrow \)(C) có PT: \({(x – 1)^2} + {(y – 2)^2} = 36\)
d) (C) có đường kính AB với A(−2 ; 3) và B(0 ; 1)
\( \Rightarrow \) (C) có tâm I là trung điểm của AB \( \Rightarrow I( – 1;2)\)
(C) có bán kính IA = IB = \(\sqrt 2 \)
\( \Rightarrow \)(C) có PT: \({(x + 1)^2} + {(y – 2)^2} = 2\)
e) (C) có tâm I thuộc đường thẳng \({\Delta _1}:\left\{ \begin{array}{l}x = 1 + t\\y = 1 – t\end{array} \right.\) và (C) tiếp xúc với hai đường thẳng ∆2: 3x + 4y – 1 = 0, ∆3: 3x – 4y + 2 = 0
Do \(I \in {\Delta _1}\) nên \(I(1 + t;1 – t)\)
Theo giả thiết, \(R = d(I,{\Delta _2}) = d(I,{\Delta _3}) \Leftrightarrow \frac{{\left| {3(1 + t) + 4(1 – t) – 1} \right|}}{{\sqrt {{3^2} + {4^2}} }} = \frac{{\left| {3(1 + t) – 4(1 – t) + 2} \right|}}{{\sqrt {{3^2} + {{( – 4)}^2}} }}\)
\( \Leftrightarrow \left| {6 – t} \right| = \left| {7t + 1} \right| \Leftrightarrow \left[ \begin{array}{l}6 – t = 7t + 1\\6 – t = – 7t – 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t = \frac{5}{8}\\t = \frac{{ – 7}}{6}\end{array} \right.\)
Với \(t = \frac{5}{8} \Rightarrow I\left( {\frac{{13}}{8};\frac{3}{8}} \right)\) \( \Rightarrow \)\(R = \frac{{43}}{{40}}\). Khi đó (C) có PT: \({\left( {x – \frac{{13}}{8}} \right)^2} + {\left( {y – \frac{3}{8}} \right)^2} = \frac{{1849}}{{1600}}\)
Với \(t = – \frac{7}{6} \Rightarrow I\left( { – \frac{1}{6};\frac{{13}}{6}} \right)\)\( \Rightarrow \)\(R = \frac{{43}}{{30}}\). Khi đó (C) có PT: \({\left( {x + \frac{1}{6}} \right)^2} + {\left( {y – \frac{{13}}{6}} \right)^2} = \frac{{1849}}{{900}}\)
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 5
Giải bài 55 trang 89 SBT Toán 10 Cánh diều tập 2 – CD
Lập phương trình đường thẳng ∆ là tiếp tuyến của đường tròn (C): (x + 2)2 + (y − 3)2 = 4 trong mỗi trường hợp sau:
a) ∆ tiếp xúc (C) tại điểm có tung độ bằng 3
b) ∆ vuông góc với đường thẳng 5x – 12y + 1 = 0
c) ∆ đi qua điểm D(0 ; 4)
Phương pháp giải
Bước 1: Tìm tọa độ tâm I của (C)
Bước 2:
a) Tham số hóa và xác định tọa độ tiếp điểm và VTPT của tiếp tuyến
b)
– Xác định tọa độ VTPT của tiếp tuyến, viết PTTQ với VTPT vừa tìm được
– Sử dụng công thức khoảng cách để tìm hệ số tự do trong PT tiếp tuyến
c)
– Viết PTTQ của tiếp tuyến biết điểm đi qua D(0 ; 4) và biểu diễn hệ số tự do theo tọa độ của VTPT
– Sử dụng công thức khoảng cách để tìm tọa độ VTPT
Bước 3: Viết PT tiếp tuyến của (C) với các yếu tố tìm được ở bước 2
Lời giải chi tiết
(C) có tâm I(-2 ; 3), bán kính R = 2
a) Theo giả thiết, điểm M(m; 3) là tiếp điểm của ∆ và (C)
Ta có: \(IM = 2 \Leftrightarrow I{M^2} = 4 \Leftrightarrow {(m + 2)^2} = 4 \Leftrightarrow \left[ \begin{array}{l}m + 2 = 2\\m + 2 = – 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 0\\m = – 4\end{array} \right.\)
Với m = 0 thì M(0 ; 3) \( \Rightarrow \)∆ đi qua M và nhận \(\overrightarrow {IM} = (2;0)\) làm VTPT nên có PT: x = 0
Với m = -4 thì M(-4 ; 3) \( \Rightarrow \)∆ đi qua M và nhận \(\overrightarrow {IM} = ( – 2;0)\) làm VTPT nên có PT: x + 4 = 0
b) Theo giả thiết, ∆ vuông góc với đường thẳng d: 5x – 12y + 1 = 0 mà d có VTPT \(\overrightarrow {{n_d}} = (5; – 12)\)
\( \Rightarrow \Delta \) nhận \(\overrightarrow n = (12;5)\) làm VTPT \( \Rightarrow \Delta \) có PTTQ: 12x + 5y + c = 0
Ta có: \(d(I,\Delta ) = R \Leftrightarrow \frac{{\left| {12.( – 2) + 5.3 + c} \right|}}{{\sqrt {{{12}^2} + {5^2}} }} = 2\)\( \Leftrightarrow \left| {c – 9} \right| = 26 \Leftrightarrow \left[ \begin{array}{l}c – 9 = 26\\c – 9 = – 26\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}c = 35\\c = – 17\end{array} \right.\)
Với c = 35 thì ∆ có PT: 12x + 5y + 35 = 0
Với c = -17 thì ∆ có PT: 12x + 5y – 17 = 0
c) Giả sử ∆ có PTTQ: \(ax + by + c = 0\)
Ta có: \(D(0;4) \in \Delta \Rightarrow 4b + c = 0 \Leftrightarrow c = – 4b\)\( \Rightarrow \Delta :ax + by – 4b = 0\)
Ta có: \(d(I,\Delta ) = R \Leftrightarrow \frac{{\left| { – 2a + 3b – 4b} \right|}}{{\sqrt {{a^2} + {b^2}} }} = 2\)\( \Leftrightarrow \left| { – 2a – b} \right| = 2\sqrt {{a^2} + {b^2}} \)
\( \Leftrightarrow 4{a^2} + 4ab + {b^2} = 4({a^2} + {b^2}) \Leftrightarrow 3{b^2} = 4ab \Leftrightarrow \left[ \begin{array}{l}b = 0\\3b = 4a\end{array} \right.\)
Với b = 0, chọn a = 1 \( \Rightarrow \Delta \) có PT: x = 0
Với 3b = 4a, chọn a = 3, b = 4 \( \Rightarrow \Delta \) có PT: 3x + 4y – 16 = 0
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 5
Giải bài 56 trang 89 SBT Toán 10 Cánh diều tập 2 – CD
Trong mặt phẳng toạ độ Oxy, cho đường tròn (C): (x + 2)2 + (y − 4)2 = 25 và điểm A(-1; 3).
a) Xác định vị trí tương đối của điểm A đối với đường tròn (C)
b) Đường thẳng d thay đổi đi qua A cắt đường tròn tại M và N. Viết phương trình đường thẳng d sao cho MN ngắn nhất
Phương pháp giải
Bước 1: Xác định tọa độ tâm I và bán kính R của (C)
Bước 2: So sánh độ dài IA và bán kính R để xét vị trí tương đối của A với (C)
Bước 3: Áp dụng tính chất dây cung càng xa tâm có độ dài càng nhỏ để tìm GTLN của \(d(I,d)\)
Bước 4: Viết PTTQ của d với các yếu tố tìm được ở bước 3
Lời giải chi tiết
a) (C) có tâm I(-2 ; 4) và bán kính R = 5
Ta có: \(\overrightarrow {IA} = (1; – 1) \Rightarrow IA = \sqrt 2 \)
Có: \(IA = \sqrt 2 < R \Rightarrow \) Điểm A nằm bên trong đường tròn (C)
b) Theo giả thiết, d cắt (C) tại 2 điểm M, N thỏa mãn MN ngắn nhất \( \Leftrightarrow \) khoảng cách từ tâm I đến d lớn nhất
Gọi H là hình chiếu của I trên d. Ta có: \(IH \le IA\)
\( \Rightarrow \) IH đạt GTLN khi và chỉ khi H trùng với A
\( \Rightarrow IA \bot d\) \( \Rightarrow d\) nhận \(\overrightarrow {IA} = (1; – 1)\) làm vectơ pháp tuyến nên có PT: x – y + 4 = 0
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 5
Giải bài 57 trang 90 SBT Toán 10 Cánh diều tập 2 – CD
Trong mặt phẳng toạ độ Oxy, cho các đường thẳng: ∆1: x + y + 1 = 0, ∆2: 3x + 4y + 20 = 0, ∆3: 2x – y + 50 = 0 và đường tròn (C): (x + 3)2 + (y −1)2 = 9. Xác định vị trí tương đối của các đường thẳng đã cho đối với đường tròn (C).
Phương pháp giải
Bước 1: Xác định tọa độ tâm I và bán kính của đường tròn (C)
Bước 2: Tính khoảng cách từ tâm I đến các đường thẳng và kết luận về vị trí tương đối của các đường thẳng đã cho với (C)
Lời giải chi tiết
(C) có tâm I(-3 ; 1) và bán kính R = 3
+) Xét ∆1: x + y + 1 = 0
Ta có: \(d(I,{\Delta _1}) = \frac{{\left| { – 3 + 1 + 1} \right|}}{{\sqrt {{1^2} + {1^2}} }} = \frac{{\sqrt 2 }}{2} < R\) \( \Rightarrow {\Delta _1}\) cắt đường tròn (C) tại 2 điểm
+) Xét ∆2: 3x + 4y + 20 = 0
Ta có: \(d(I,{\Delta _2}) = \frac{{\left| {3.( – 3) + 4.1 + 20} \right|}}{{\sqrt {{3^2} + {4^2}} }} = 3 = R\) \( \Rightarrow {\Delta _2}\) tiếp xúc với đường tròn (C)
+ Xét ∆3: 2x – y + 50 = 0
Ta có: \(d(I,{\Delta _3}) = \frac{{\left| {2.( – 3) – 1 + 50} \right|}}{{\sqrt {{2^2} + {{( – 1)}^2}} }} = \frac{{43\sqrt 5 }}{5} > R\) \( \Rightarrow {\Delta _3}\) và đường tròn (C) không giao nhau
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 5
Giải bài 58 trang 90 SBT Toán 10 Cánh diều tập 2 – CD
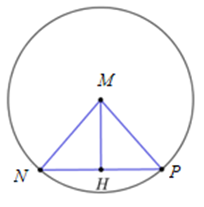
Trong mặt phẳng toạ độ Oxy, cho điểm M(1 ; 1) và đường thẳng: 3x + 4y + 3 = 0. Viết phương trình đường tròn (C), biết (C) có tâm M và đường thẳng ∆ cắt (C) tại hai điểm N, P thoả mãn tam giác MNP đều.
Phương pháp giải
Tìm bán kính đường tròn (C)
Bước 1: Tính khoảng cách từ M đến ∆
Bước 2: Xét ∆MNP đều biết độ dài đường cao kẻ từ M, tính độ dài các cạnh của tam giác là bán kính của (C)
Bước 3: Viết PT đường tròn với tâm M và bán kính tìm được ở bước 2
Lời giải chi tiết

Gọi H là hình chiếu của M lên đường thẳng ∆
Ta có: \(MH = d(M,\Delta ) = \frac{{\left| {3 + 4 + 3} \right|}}{{\sqrt {{3^2} + {4^2}} }} = 2\)
Theo giả thiết, ∆MNP đều \( \Rightarrow \widehat {MNH} = {60^0}\)
Xét \(\Delta MNH\) vuông tại H có \(MN = \frac{{MH}}{{\sin \widehat {MNH}}} = \frac{2}{{\sin {{60}^0}}} = \frac{{4\sqrt 3 }}{3}\)\( \Rightarrow R = \frac{{4\sqrt 3 }}{3}\)
Vậy (C) có PT: \({(x – 1)^2} + {(y – 1)^2} = \frac{{16}}{3}\)
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 5
=======
THUỘC: Giải sách bài tập toán 10 – Cánh diều
