GIẢI CHI TIẾT Giải SBT Bài 1 Chương 7 – SBT Toán 10 CÁNH DIỀU
===========
Giải bài 1 trang 61 SBT Toán 10 Cánh diều tập 2 – CD
Toạ độ của vectơ \(\overrightarrow u = – 3\overrightarrow i + 2\overrightarrow j \) là:
A. \(( – 3;2)\)
B. \((2; – 3)\)
C. \(( – 3\overrightarrow i ;2\overrightarrow j )\)
D. \((3;2)\)
Phương pháp giải
Áp dụng định lí: Nếu \(\overrightarrow u = a\overrightarrow i + b\overrightarrow j \) thì \(\overrightarrow u = (a;b)\)
Lời giải chi tiết
Do \(\overrightarrow u = – 3\overrightarrow i + 2\overrightarrow j \) nên \(\overrightarrow u = ( – 3;2)\)
Chọn A
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 1
Giải bài 2 trang 61 SBT Toán 10 Cánh diều tập 2 – CD
Tọa độ của vectơ \(\overrightarrow u = 5\overrightarrow j \) là:
A. \((5;0)\)
B. \((5;\overrightarrow j )\)
C. \((0;5\overrightarrow j )\)
D. \((0;5)\)
Phương pháp giải
Áp dụng định lí: Nếu \(\overrightarrow u = a\overrightarrow i + b\overrightarrow j \) thì \(\overrightarrow u = (a;b)\)
Lời giải chi tiết
Ta có: \(\overrightarrow u = 5\overrightarrow j = 0.\overrightarrow i + 5\overrightarrow j \Rightarrow \overrightarrow u = (0;5)\)
Chọn D
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 1
Giải bài 3 trang 61 SBT Toán 10 Cánh diều tập 2 – CD
Trong mặt phẳng toạ độ Oxy, cho A(2; −5). Toạ độ của vectơ \(\overrightarrow {OA} \) là:
A. (2 ; 5)
B. (2; −5)
C. (−2; −5)
D. (−2; 5)
Phương pháp giải
Áp dụng định nghĩa tọa độ điểm M được gọi là tọa độ của vectơ \(\overrightarrow {OM} \)
Lời giải chi tiết
Do A(2;− 5) nên \(\overrightarrow {OA} = (2; – 5)\)
Chọn B
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 1
Giải bài 4 trang 61 SBT Toán 10 Cánh diều tập 2 – CD
Trong mặt phẳng toạ độ Oxy, cho A(−1; 3), B(2; −1). Toạ độ của vectơ \(\overrightarrow {AB} \) là:
A. (1; -4)
B. (-3; 4)
C. (3; -4)
D. (1; -2)
Phương pháp giải
Nếu \(A({x_A};{y_A}),B({x_B};{y_B})\) thì \(\overrightarrow {AB} = ({x_B} – {x_A};{y_B} – {y_A})\)
Lời giải chi tiết
Ta có: A(−1; 3), B(2; −1) \( \Rightarrow \overrightarrow {AB} = (3; – 4)\)
Chọn C
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 1
Giải bài 5 trang 61 SBT Toán 10 Cánh diều tập 2 – CD
Trong mặt phẳng toạ độ Oxy, cho \(\overrightarrow u = ( – 2; – 4),\overrightarrow v = (2x – y;y)\). Hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) bằng nhau nếu:
A.\(\left\{ \begin{array}{l}x = 1\\y = – 4\end{array} \right.\)
B. \(\left\{ \begin{array}{l}x = – 3\\y = – 4\end{array} \right.\)
C. \(\left\{ \begin{array}{l}x = 1\\y = 4\end{array} \right.\)
D. \(\left\{ \begin{array}{l}x = – 3\\y = 4\end{array} \right.\)
Phương pháp giải
\(\overrightarrow a = ({x_1};{y_1})\) và \(\overrightarrow b = ({x_2};{y_2})\) bằng nhau khi và chỉ khi \(\left\{ \begin{array}{l}{x_1} = {x_2}\\{y_1} = {y_2}\end{array} \right.\)
Lời giải chi tiết
Ta có: \(\overrightarrow u = \overrightarrow v \Leftrightarrow \left\{ \begin{array}{l}2x – y = – 2\\y = – 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = – 3\\y = – 4\end{array} \right.\)
Chọn B
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 1
Giải bài 6 trang 61 SBT Toán 10 Cánh diều tập 2 – CD
Cho hình bình hành ABCD có A(–1 ; –2), B(3; 2), C(4; − 1). Toạ độ của đỉnh D là:
A. (8; 3)
B. (3; 8)
C. (-5; 0)
D. (0; -5)
Phương pháp giải
Bước 1: Tham số hóa tọa độ điểm D và xác định tọa độ vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {DC} \)
Bước 2: Áp dụng kết quả tứ giác ABCD là hình bình hành khi và chỉ khi \(\overrightarrow {DC} = \overrightarrow {AB} \) để tìm tọa độ điểm D
Lời giải chi tiết
Giả sử D(a; b) ta có \(\overrightarrow {DC} = (4 – a; – 1 – b)\) và \(\overrightarrow {AB} = (4;4)\)
ABCD là hình bình hành \( \Leftrightarrow \overrightarrow {DC} = \overrightarrow {AB} \Leftrightarrow \left\{ \begin{array}{l}4 – a = 4\\ – 1 – b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 0\\b = – 5\end{array} \right. \Rightarrow D(0; – 5)\)
Chọn D
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 1
Giải bài 7 trang 61 SBT Toán 10 Cánh diều tập 2 – CD
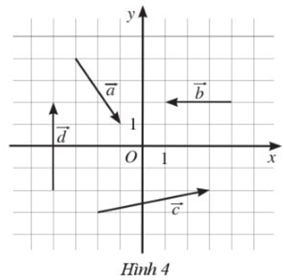
Tìm toạ độ của các vectơ trong Hình 4.

Phương pháp giải
Bước 1: Xác định tọa độ các điểm A, B, C, D sao cho \(\overrightarrow {OA} = \overrightarrow a ;\overrightarrow {OB} = \overrightarrow b ;\overrightarrow {OC} = \overrightarrow c ;\overrightarrow {OD} = \overrightarrow d \)
Bước 2: Tìm tọa độ các vectơ \(\overrightarrow a ;\overrightarrow b ;\overrightarrow c ;\overrightarrow d \) dựa vào tọa độ các vectơ \(\overrightarrow {OA} ;\overrightarrow {OB} ;\overrightarrow {OC} ;\overrightarrow {OD} \)
Lời giải chi tiết
– Vẽ \(\overrightarrow {OA} = \overrightarrow a \), ta có \(A(2; – 3)\) nên \(\overrightarrow a = (2; – 3)\)
– Vẽ \(\overrightarrow {OB} = \overrightarrow b \), ta có \(B( – 3;0)\) nên \(\overrightarrow b = ( – 3;0)\)
– Vẽ \(\overrightarrow {OC} = \overrightarrow c \), ta có \(C(5;1)\) nên \(\overrightarrow c = (5;1)\)
– Vẽ \(\overrightarrow {OD} = \overrightarrow d \), ta có \(D(0;4)\) nên \(\overrightarrow d = (0;4)\)
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 1
Giải bài 8 trang 62 SBT Toán 10 Cánh diều tập 2 – CD
Tìm các số thực a và b sao cho mỗi cặp vectơ sau bằng nhau:
a) \(\overrightarrow m = (2a + 3;b – 1)\) và \(\overrightarrow n = (1; – 2)\)
b) \(\overrightarrow u = (3a – 2;5)\)và \(\overrightarrow v = (5;2b + 1)\)
c) \(\overrightarrow x = (2a + b;2b)\) và \(\overrightarrow y = (3 + 2b;b – 3a)\)
Phương pháp giải
\(\overrightarrow a = ({x_1};{y_1})\) và \(\overrightarrow b = ({x_2};{y_2})\) bằng nhau khi và chỉ khi \(\left\{ \begin{array}{l}{x_1} = {x_2}\\{y_1} = {y_2}\end{array} \right.\)
Lời giải chi tiết
a) \(\overrightarrow m = (2a + 3;b – 1)\) và \(\overrightarrow n = (1; – 2)\)
\(\overrightarrow m = \overrightarrow n \Leftrightarrow \left\{ \begin{array}{l}2a + 3 = 1\\b – 1 = – 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = – 1\\b = – 1\end{array} \right.\)
b) \(\overrightarrow u = (3a – 2;5)\)và \(\overrightarrow v = (5;2b + 1)\)
\(\overrightarrow u = \overrightarrow v \Leftrightarrow \left\{ \begin{array}{l}3a – 2 = 5\\5 = 2b + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{7}{3}\\b = 2\end{array} \right.\)
c) \(\overrightarrow x = (2a + b;2b)\) và \(\overrightarrow y = (3 + 2b;b – 3a)\)
\(\overrightarrow x = \overrightarrow y \Leftrightarrow \left\{ \begin{array}{l}2a + b = 3 + 2b\\2b = b – 3a\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2a – b = 3\\3a + b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{3}{5}\\b = – \frac{9}{5}\end{array} \right.\)
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 1
Giải bài 9 trang 62 SBT Toán 10 Cánh diều tập 2 – CD
Trong mặt phẳng toạ độ Oxy, cho ba điểm không thẳng hàng A(– 4 ; 2), B(2 ; 4), C(8 ; – 2). Tìm toạ độ của điểm D sao cho tứ giác ABCD là hình bình hành.
Phương pháp giải
Bước 1: Tham số hóa tọa độ điểm D và xác định tọa độ vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {DC} \)
Bước 2: Áp dụng kết quả tứ giác ABCD là hình bình hành khi và chỉ khi \(\overrightarrow {DC} = \overrightarrow {AB} \) để tìm tọa độ điểm D
Lời giải chi tiết
Giả sử D(a; b) ta có \(\overrightarrow {DC} = (8 – a; – 2 – b)\) và \(\overrightarrow {AB} = (6;2)\)
ABCD là hình bình hành \( \Leftrightarrow \overrightarrow {DC} = \overrightarrow {AB} \Leftrightarrow \left\{ \begin{array}{l}8 – a = 6\\ – 2 – b = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = – 4\end{array} \right. \Rightarrow D(2; – 4)\)
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 1
Giải bài 10 trang 62 SBT Toán 10 Cánh diều tập 2 – CD
Trong mặt phẳng toạ độ Oxy, cho tứ giác ABCD có \(A({x_A};{y_A});B({x_B};{y_B});C({x_C};{y_C});D({x_D};{y_D})\). Chứng minh rằng tứ giác ABCD là hình bình hành khi và chỉ khi \({x_A} + {x_C} = {x_B} + {x_D}\) và \({y_A} + {y_C} = {y_B} + {y_D}\)
Phương pháp giải
Bước 1: Xxác định tọa độ vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {DC} \)
Bước 2: Áp dụng kết quả tứ giác ABCD là hình bình hành khi và chỉ khi \(\overrightarrow {DC} = \overrightarrow {AB} \) để chứng minh
Lời giải chi tiết
Ta có: \(\overrightarrow {AB} = ({x_B} – {x_A};{y_B} – {y_A})\) và \(\overrightarrow {DC} = ({x_C} – {x_D};{y_C} – {y_D})\)
ABCD là hình bình hành \( \Leftrightarrow \overrightarrow {AB} = \overrightarrow {CD} \Leftrightarrow \left\{ \begin{array}{l}{x_B} – {x_A} = {x_C} – {x_D}\\{y_B} – {y_A} = {y_C} – {y_D}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_B} + {x_D} = {x_C} + {x_A}\\{y_B} + {y_D} = {y_C} + {y_A}\end{array} \right.\) (ĐPCM)
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 1
Giải bài 11 trang 62 SBT Toán 10 Cánh diều tập 2 – CD
Trong mặt phẳng toạ độ Oxy, cho ba điểm không thẳng hàng M(1 ; – 2), N(3 ; 1), P(− 1 ; 2). Tìm toạ độ điểm Q sao cho tứ giác MNPQ là hình thang có MN // PQ và PQ = 2MN.
Phương pháp giải
Từ giả thiết tìm tọa độ điểm Q thỏa mãn \(\overrightarrow {PQ} = 2\overrightarrow {NM} \)
Lời giải chi tiết
Ta có: MN // PQ nên \(\overrightarrow {MN} \) và \(\overrightarrow {PQ} \) cùng phương
Mặt khác, PQ = 2MN \( \Rightarrow \overrightarrow {PQ} = 2\overrightarrow {NM} \)
Gọi tọa độ điểm Q là \(Q(a;b)\). Ta có: \(\overrightarrow {PQ} = (a + 1;b – 2)\) và \(\overrightarrow {NM} = ( – 2; – 3)\)
\( \Rightarrow \overrightarrow {PQ} = 2\overrightarrow {NM} \Leftrightarrow \left\{ \begin{array}{l}a + 1 = 2.( – 2)\\b – 2 = 2.( – 3)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a + 1 = – 4\\b – 2 = – 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = – 5\\b = – 4\end{array} \right.\) . Vậy Q(-5 ; -4)
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 1
=======
THUỘC: Giải sách bài tập toán 10 – Cánh diều
