Giải SBT bài 4 Định lí và chứng minh một định lí (C4 Toán 7 – Chân trời)

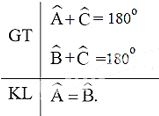
Giải SBT bài 4 Định lí và chứng minh một định lí (C4 Toán 7 – Chân trời)
————

Giải bài 1 trang 86 SBT Toán 7 Chân trời sáng tạo tập 1 – CTST

Ta gọi hai góc có tổng bằng 180° là hai góc bù nhau. Hãy viết giả thiết, kết luận bằng kí hiệu và chứng minh định lí: “Hai góc cùng bù một góc thứ ba thì hai góc đó bằng nhau”.

Hướng dẫn giải chi tiết Bài 1

Phương pháp giải

Viết giả thiết và kết luận bằng kí hiệu:

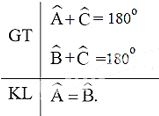
Lời giải chi tiết

Chứng minh định lí:

Theo GT ta có:

\(\widehat A\) bù với \(\widehat C\) nên \(\widehat A\)+\(\widehat C\)=180°

Suy ra \(\widehat A\)=180° − \(\widehat C\) (1)

\(\widehat B\) bù với \(\widehat C\) nên \(\widehat B+\widehat C\)=180°

Suy ra \(\widehat B\)=180° − \(\widehat C\) (2)

Từ (1) và (2) suy ra \(\widehat A\)=\(\widehat B\)

Vậy \(\widehat A\)=\(\widehat B\)

 

–>

— *****

Giải bài 2 trang 86 SBT Toán 7 Chân trời sáng tạo tập 1 – CTST

Cho định lí “Hai góc đối đỉnh thì bằng nhau”.

a) Hãy vẽ hình minh hoạ, phát biểu giả thiết của định lí trên.

b) Hãy chứng minh định lí đó.

Hướng dẫn giải chi tiết Bài 2

Phương pháp giải

Chứng minh định lí là dùng lập luận để từ giả thiết và những khẳng định đúng đã biết suy ra kết luận của định lí.

Lời giải chi tiết

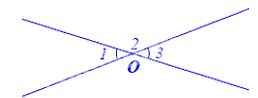
a) Hình vẽ minh họa:

Viết giả thiết và kết luận bằng kí hiệu:

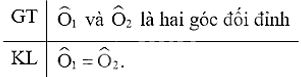
b) Chứng minh định lí:

Ta có:

\(\widehat {{O_1}}\) và \(\widehat {{O_3}}\) là hai góc kề bù nên

\(\widehat {{O_1}}\)+\(\widehat {{O_3}}\)=180°

Suy ra \(\widehat {{O_1}}\)=180°−\(\widehat {{O_3}}\) (1)

\(\widehat {{O_2}}\) và \(\widehat {{O_3}}\) là hai góc kề bù nên

\(\widehat {{O_2}}\)+\(\widehat {{O_3}}\)=180°

Suy ra \(\widehat {{O_2}}\)=180°−\(\widehat {{O_3}}\) (2)

Từ (1) và (2) suy ra \(\widehat {{O_1}}\)=\(\widehat {{O_2}}\).

Vậy \(\widehat {{O_1}}\)=\(\widehat {{O_2}}\).

 

–>

— *****

Giải bài 3 trang 86 SBT Toán 7 Chân trời sáng tạo tập 1 – CTST

Chứng minh định lí: “Góc tạo bởi hai tia phân giác của hai góc kề bù là một góc vuông”.Chứng minh định lí: “Góc tạo bởi hai tia phân giác của hai góc kề bù là một góc vuông”.

Hướng dẫn giải chi tiết Bài 3

Phương pháp giải

Chứng minh định lí là dùng lập luận để từ giả thiết và những khẳng định đúng đã biết suy ra kết luận của định lí.

Lời giải chi tiết

Hình vẽ minh họa:

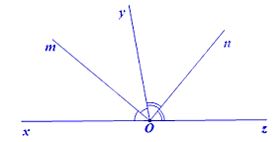
Viết giả thiết và kết luận bằng kí hiệu:

Chứng minh định lí:

Vì tia Om là tia phân giác của \(\widehat {xOy}\) nên ta có:

\(\widehat {xOm}\)=\(\widehat {mOy}\)=\(\dfrac{1}{2}\)\(\widehat {xOy}\) (1)

Vì tia On là tia phân giác của \(\widehat {yOz}\) nên ta có:

\(\widehat {yOn}\)=\(\widehat {nOz}\)=\(\dfrac{1}{2}\)\(\widehat {yOz}\) (2)

Từ (1) và (2) ta có:

\(\widehat {mOy} + \widehat {yOn} = \dfrac{1}{2}\widehat {xOy} + \dfrac{1}{2}\widehat {yOz} = \dfrac{1}{2}(\widehat {xOy} + \widehat {yOz})\)

Mà \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề bù nên:

\(\widehat {xOy}\)+\(\widehat {yOz}\)=180°

Do đó \(\widehat {mOy}\)+\(\widehat {yOn}\)=\(\dfrac{1}{2}\).180°=90°

Hay \(\widehat {mOn}\)=90°.

Vậy \(\widehat {mOn}\)=90° 

 

–>

— *****

Giải bài 4 trang 86 SBT Toán 7 Chân trời sáng tạo tập 1 – CTST

Chứng minh định lí: “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau”.

Hướng dẫn giải chi tiết Bài 4

Phương pháp giải

Sử dụng dấu hiệu nhận biết 2 đường thẳng song song.

Lời giải chi tiết

Hình vẽ minh họa:

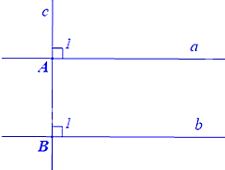
Viết giả thiết và kết luận bằng kí hiệu:

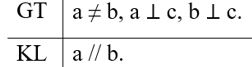
Chứng minh định lí:

Vì a ⊥ c (GT) nên \(\widehat {{A_1}}\)=90°

Vì b ⊥ c (GT) nên \(\widehat {{B_1}}\)=90°

Do đó \(\widehat {{A_1}}\) = \(\widehat {{B_1}}\) (=90°)

Mà \(\widehat {{A_1}}\) và \(\widehat {{B_1}}\) ở vị trí đồng vị

Suy ra a // b (Dấu hiệu nhận biết 2 đường thẳng song song).

Vậy a // b.

 

–>

— *****

Giải bài 5 trang 86 SBT Toán 7 Chân trời sáng tạo tập 1 – CTST

Hãy phát biểu phần kết luận còn thiếu của các định lí sau:

a) Hai góc cùng phụ một góc thứ ba thì .?.

b) Nếu hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì ?

Hướng dẫn giải chi tiết Bài 5

Phương pháp giải

Xem lại định lí ở SGK

Lời giải chi tiết

a) Hai góc cùng phụ một góc thứ ba thì  bằng nhau .

b) Nếu hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì  hai đường thẳng đó song song với nhau .

 

–>

— *****