Giải SBT bài 1 Các góc ở vị trí đặc biệt (C4 Toán 7 – Chân trời)

Giải SBT bài 1 Các góc ở vị trí đặc biệt (C4 Toán 7 – Chân trời)
========

Giải bài 1 trang 75 SBT Toán 7 Chân trời sáng tạo tập 1 – CTST

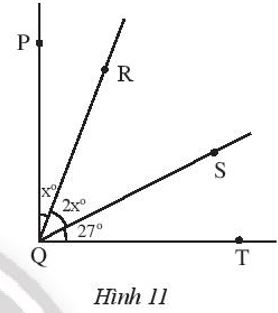
Cho Hình 11

a) Tìm các góc kề với \(\widehat {RQS}\)

b) Cho biết \(\widehat {PQT}\)=90°. Tìm số đo của các góc \(\widehat {RQS}\) và \(\widehat {RQP}\)

Hướng dẫn giải chi tiết Bài 1

Phương pháp giải

Ta sử dụng định nghĩa về 2 góc kề nhau và tính chất các góc phụ nhau để tìm x 

Lời giải chi tiết

a) Các góc kề với \(\widehat {RQS}\) là: \(\widehat {PQR}\) và \(\widehat {SQT}\)

b) Vì \(\widehat {RQS}\) kề với \(\widehat {PQR}\) và \(\widehat {SQT}\)nên ta có:

\(\widehat {RQS} + \widehat {PQR} + \widehat {SQT} = \widehat {PQT}\)

Hay x° + 2x° + 27° = 90°

Suy ra 3x° = 63°

Do đó x° = 21°.

Suy ra 2x° = 2.21° = 42°.

Vậy \(\widehat {RQS}\) = 2x° = 42° và \(\widehat {PQR}\) = x° = 21°.

 

–>

— *****

Giải bài 2 trang 75 SBT Toán 7 Chân trời sáng tạo tập 1 – CTST

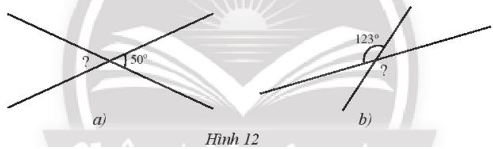
Tìm số đo góc có dấu “?” trong Hình 12.

Hướng dẫn giải chi tiết Bài 2

Phương pháp giải

Ta thấy các góc cần tìm đều là góc đối đỉnh với 1 góc có sẵn số đo

Lời giải chi tiết

a)

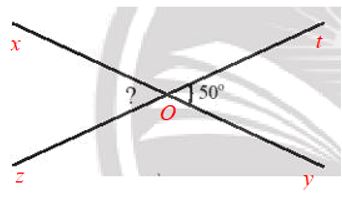
Giả sử đường thẳng xy cắt zt tạo điểm O tạo thành \(\widehat {tOy}\) =50° như hình vẽ.

Ta cần đi tìm số đo của góc \(\widehat {xOz}\)

Ta có: \(\widehat {xOz}\) và \(\widehat {tOy}\) là hai góc đối đỉnh.

Nên \(\widehat {xOz}\) =\(\widehat {tOy}\) =50°.

Vậy \(\widehat {xOz}\)= 50°.

b)

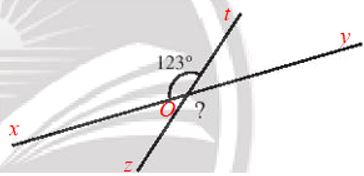
Giả sử đường thẳng xy cắt zt tạo điểm O tạo thành \(\widehat {xOt}\)= 123° như hình vẽ.

Ta cần đi tìm số đo của góc \(\widehat {zOy}\).

Ta có: \(\widehat {xOt}\) và \(\widehat {zOy}\) là hai góc đối đỉnh.

Nên \(\widehat {zOy}\)=\(\widehat {xOt}\)=123°.

Vậy \(\widehat {zOy}\)=123°

 

–>

— *****

Giải bài 3 trang 75 SBT Toán 7 Chân trời sáng tạo tập 1 – CTST

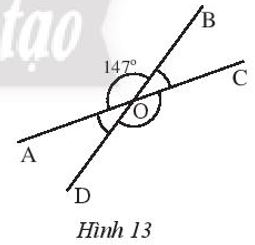
Tìm số đo các góc chưa biết trong Hình 13.

Hướng dẫn giải chi tiết Bài 3

Phương pháp giải

Ta sử dụng tính chất 2 góc đối đỉnh và các góc kề bù để tìm số đo các góc chưa biết trong hình.

Lời giải chi tiết

Ta có: \(\widehat {AOB}\) và \(\widehat {COD}\) là hai góc đối đỉnh nên:

\(\widehat {COD}\)=\(\widehat {AOB}\) = 147°

Vì \(\widehat {AOB}\) và \(\widehat {BOC}\) là hai góc kề bù nên:

\(\widehat {AOB}\)+\(\widehat {BOC}\) = 180°

Suy ra \(\widehat {BOC}\)=180°−\(\widehat {AOB}\) = 180°−147° = 33°.

Ta lại có: \(\widehat {BOC}\) và \(\widehat {AOD}\) là hai góc đối đỉnh nên:

\(\widehat {AOD}\)=\(\widehat {BOC}\) = 33°.

Vậy \(\widehat {BOC}\) = 33°,\(\widehat {COD}\) = 147° và \(\widehat {AOD}\) = 33°. 

 

–>

— *****

Giải bài 4 trang 75 SBT Toán 7 Chân trời sáng tạo tập 1 – CTST

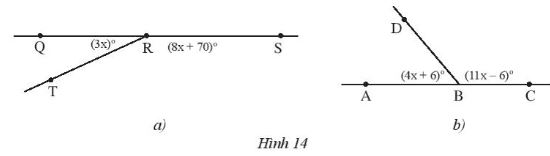
Tìm giá trị của x trong Hình 14

Hướng dẫn giải chi tiết Bài 4

Phương pháp giải

Ta sử dụng tính chất của 2 góc kề bù để tìm x

Lời giải chi tiết

a) Vì \(\widehat {QRT}\) và \(\widehat {TRS}\)là hai góc kề bù nên:

\(\widehat {QRT}\)+\(\widehat {TRS}\)=180°

Suy ra (3x)° + (8x + 70)° = 180°

Nên (3x + 8x + 70)° = 180°

Do đó 11x + 70 = 180

Suy ra 11x = 110

Suy ra x = 10.

Vậy x = 10.

b) Vì \(\widehat {ABD}\) và \(\widehat {DBC}\) là hai góc kề bù nên:

\(\widehat {ABD}\)+\(\widehat {DBC}\)=180°

Suy ra (4x + 6)° + (11x – 6)° = 180°

Nên (4x + 6 + 11x – 6)° = 180°

Do đó 15x = 180

Suy ra x = 12.

Vậy x = 12 

 

–>

— *****

Giải bài 5 trang 75 SBT Toán 7 Chân trời sáng tạo tập 1 – CTST

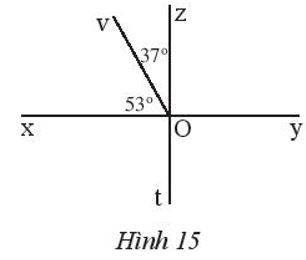
Cho Hình 15 chứng minh hai đường thẳng xy và zt vuông góc.

Hướng dẫn giải chi tiết Bài 5

Phương pháp giải

Ta sử dụng tính chất 2 góc kề nhưng ở đây ta thấy chúng còn là kề bù để chứng minh 2 đường thẳng vuông góc

Lời giải chi tiết

Vì \(\widehat {xOv}\) và \(\widehat {vOz}\)là hai góc kề nhau nên:

\(\widehat {xOv}\)+\(\widehat {vOz}\)=\(\widehat {xOz}\)

Do đó \(\widehat {xOz}\)=53°+37°=90°

Suy ra Ox ⊥ Oz hay xy ⊥ zt.

Vậy hai đường thẳng xy và zt vuông góc.

 

–>

— *****