Giải SBT Bài 3: Phép cộng và phép trừ đa thức một biến (C7 SBT Toán 7 Chân trời)

Giải SBT Bài 3: Phép cộng và phép trừ đa thức một biến (C7 SBT Toán 7 Chân trời)
———

Giải bài 1 trang 30 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Cho hai đa thức \(P\left( x \right) =  – 4{x^4} – 3{x^2} + 7\) và \(Q\left( x \right) = 2{x^4} – 5{x^2} + 8x – 1\). Hãy tính \(P\left( x \right) + Q\left( x \right)\) và \(P\left( x \right) – Q\left( x \right)\).

Hướng dẫn giải chi tiết Bài 1

Phương pháp giải

Bước 1: Thực hiện cộng trừ các đơn thức cùng một biến để rút gọn đa thức đã cho.

Bước 2: Sắp xếp các đơn thức theo lũy thừa giảm dần của biến.

Bước 3: Thực hiện phép tính theo hàng ngang hoặc cột dọc.

Lời giải chi tiết

\(P\left( x \right) + Q\left( x \right) =  – 4{x^4} – 3{x^2} + 7 + 2{x^4} – 5{x^2} + 8x – 1 =  – 2{x^4} – 8{x^2} + 8x + 6\)

\(P\left( x \right) – Q\left( x \right) =  – 4{x^4} – 3{x^2} + 7 – \left( {2{x^4} – 5{x^2} + 8x – 1} \right) =  – 6{x^4} + 2{x^2} – 8x + 8\).

 

–>

— *****

Giải bài 2 trang 30 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Cho đa thức \(A\left( t \right) = 2{t^4} – 8{t^3} + 9t + 3\). Tìm đa thức \(B\left( t \right)\) sao cho \(B\left( t \right) – A\left( t \right) =  – 4{t^3} + 3{t^2} + 8t\).

Hướng dẫn giải chi tiết Bài 2

Phương pháp giải

Bước 1: Thực hiện cộng trừ các đơn thức cùng một biến để rút gọn đa thức đã cho.

Bước 2: Sắp xếp các đơn thức theo lũy thừa giảm dần của biến.

Bước 3: Thực hiện phép tính theo hàng ngang hoặc cột dọc.

Lời giải chi tiết

\(\begin{array}{l}B\left( t \right) – A\left( t \right) =  – 4{t^3} + 3{t^2} + 8t \Rightarrow B\left( t \right) =  – 4{t^3} + 3{t^2} + 8t + A\left( t \right)\\ =  – 4{t^3} + 3{t^2} + 8t + 2{t^4} – 8{t^3} + 9t + 3 = 2{t^4} – 12{t^3} + 3{t^2} + 17t + 3\end{array}\)

Vậy \(B\left( t \right) = 2{t^4} – 12{t^3} + 3{t^2} + 17t + 3\).

 

–>

— *****

Giải bài 3 trang 30 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Cho đa thức \(M\left( x \right) = 4{x^3} – 7{x^2} + 2x – 9\). Tìm đa thức \(N\left( x \right)\) sao cho \(M\left( x \right) + N\left( x \right) = 2{x^3} – 6x\).

Hướng dẫn giải chi tiết Bài 3

Phương pháp giải

Bước 1: Thực hiện cộng trừ các đơn thức cùng một biến để rút gọn đa thức đã cho.

Bước 2: Sắp xếp các đơn thức theo lũy thừa giảm dần của biến.

Bước 3: Thực hiện phép tính theo hàng ngang hoặc cột dọc.

Lời giải chi tiết

Ta có \(M\left( x \right) + N\left( x \right) = 2{x^3} – 6x \Rightarrow N\left( x \right) = 2{x^3} – 6x – M\left( x \right) = 2{x^3} – 6x – \left( {4{x^3} – 7{x^2} + 2x – 9} \right)\)\( – 2{x^3} + 7{x^2} – 8x + 9\)

Vậy \(N\left( x \right) =  – 2{x^3} + 7{x^2} – 8x + 9\)

 

–>

— *****

Giải bài 4 trang 30 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Cho ba đa thức \(P\left( x \right) = 3{x^4} – 2{x^2} + 8x – 10\); \(Q\left( x \right) = 4{x^3} – 6{x^2} + 7x – 1\) và \(R\left( x \right) =  – 3{x^4} + 5{x^2} – 8x – 5\). Tính \(P\left( x \right) + Q\left( x \right) + R\left( x \right)\) và \(P\left( x \right) – Q\left( x \right) – R\left( x \right)\).

Hướng dẫn giải chi tiết bài 4

Phương pháp giải

Bước 1: Thực hiện cộng trừ các đơn thức cùng một biến để rút gọn đa thức đã cho.

Bước 2: Sắp xếp các đơn thức theo lũy thừa giảm dần của biến.

Bước 3: Thực hiện phép tính theo hàng ngang hoặc cột dọc.

Lời giải chi tiết

\(\begin{array}{*{20}{c}}{}&{3{x^4}}&{}&{}& – &{2{x^2}}& + &{8x}& – &{10}\\ + &{}&{}&{}&{}&{}&{}&{}&{}&{}\\{}&{}&{}&{4{x^3}}& – &{6{x^2}}& + &{7x}& – &1\\ + &{}&{}&{}&{}&{}&{}&{}&{}&{}\\{}&{ – 3{x^4}}&{}&{}& + &{5{x^2}}& – &{8x}& – &5\\\hline{}&{}&{}&{4{x^3}}& – &{3{x^2}}& + &{7x}& – &{16}\end{array}\)

Vậy \(P\left( x \right) + Q\left( x \right) + R\left( x \right) = 4{x^3} – 3{x^2} + 7x – 16\)

\(\begin{array}{*{20}{c}}{}&{3{x^4}}&{}&{}& – &{2{x^2}}& + &{8x}& – &{10}\\ – &{}&{}&{}&{}&{}&{}&{}&{}&{}\\{}&{}&{}&{4{x^3}}& – &{6{x^2}}& + &{7x}& – &1\\ – &{}&{}&{}&{}&{}&{}&{}&{}&{}\\{}&{ – 3{x^4}}&{}&{}& + &{5{x^2}}& – &{8x}& – &5\\\hline{}&{6{x^4}}& – &{4{x^3}}& – &{{x^2}}& + &{9x}& – &4\end{array}\)

Vậy \(P\left( x \right) – Q\left( x \right) – R\left( x \right) = 6{x^4} – 4{x^3} – {x^2} + 9x – 4\).

 

–>

— *****

Giải bài 5 trang 30 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Cho đa thức \(P\left( x \right) =  – 3{x^2} + 7x – 5\). Hãy viết \(P\left( x \right)\) thành tổng của hai đa thức bậc bốn.

Hướng dẫn giải chi tiết Bài 5

Phương pháp giải

Bậc của đa thức \(P\left( x \right)\) là 2, do đó để viết \(P\left( x \right)\) thành tổng của hai đa thức bậc bốn, thì hai đơn thức bậc bốn phải có hệ số trái dấu nhau

Lời giải chi tiết

\(P\left( x \right) = \left( {2{x^4} + 4{x^2} + 2x – 1} \right) + \left( { – 2{x^4} – 7{x^2} + 5x – 4} \right) =  – 3{x^2} + 7x – 5\)

 

–>

— *****

Giải bài 6 trang 30 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

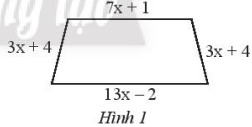
Viết biểu thức biểu thị chu vi của hình thang cân trong Hình 1.

Hướng dẫn giải chi tiết Bài 6

Phương pháp giải

Sử dụng các công thức đã học về chu vi của hình thang để viết biểu thức.

Lời giải chi tiết

Chu vi hình thang bằng tổng của bốn cạnh. Do đó ta có biểu thức

\(7x + 1 + 3x + 4 + 13x – 2 + 3x + 4 = 26x + 7\).

 

–>

— *****

Giải bài 7 trang 30 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Cho tam giác (xem Hình 2) có chu vi bằng \(12t – 6\), Hãy tìm cạnh chưa biết của tam giác đó

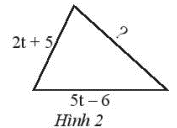
Hướng dẫn giải chi tiết Bài 7

Phương pháp giải

Chu vi của tam giác bằng tổng ba cạnh của tam giác đó. Nên muốn tìm cạnh chưa biết ta lấy chu vi trừ đi các cạnh đã biết.

Lời giải chi tiết

Biểu thức biểu thị cạnh chưa biết là:

\(12t – 6 – \left( {2t + 5} \right) – \left( {5t – 6} \right) = 5t – 5\).

 

–>

— *****

Giải bài 8 trang 30 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

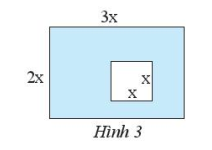
Hãy viết biểu thức biểu thị diện tích của phần tô đậm trong Hình 3.

Hướng dẫn giải chi tiết Bài 8

Phương pháp giải

Sử dụng các công thức tính diện tích đã học để viết được biểu thức.

Diện tích hình chữ nhật bằng tích chiều dài và chiều rộng

Diện tích hình vuông bằng cạnh bình phương.

Lời giải chi tiết

Diện tích hình chữ nhật là \(2x.3x = 6{x^2}\)

Diện tích hình vuông là \({x^2}\)

Diện tích phần tô đậm là \(6{x^2} – {x^2} = 5{x^2}\).

 

–>

— *****

Giải bài 9 trang 31 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Số lượng xe du lịch được bán ra tại một nước từ năm 1983 tới năm 1996 được mô tả theo công thức \(C =  – 0,016{t^4} + 0,49{t^3} – 4,8{t^2} + 14t + 70\) (tính bằng đơn vị nghìn chiếc), trong khi đó số xe tải thì tính theo \(T =  – 0,01{t^4} + 0,31{t^3} – 3{t^2} + 11t + 23\), với t là số năm tính từ 1983. Viết biểu thức biểu thị số xe (cả xe du lịch và xe tải) được bán ra trong khoảng thời gian nêu trên. Tính số xe được bán ra vào năm 1990 (ứng với \(t = 7\)).

Hướng dẫn giải chi tiết Bài 9

Phương pháp giải

Thực hiện phép cộng đa thức một biến

Bước 1: Sắp xếp các đơn thức của hai đa thức cùng theo thứ tự lũy thừa giảm dần (hoặc tăng dần) của biến.

Bước 2: Thực hiện phép tính theo hàng ngang hoặc cột dọc.

Lời giải chi tiết

Biểu thức biểu thị số xe (cả xe du lịch và xe tải) được bán ra từ năm 1983 đến năm 1996 là

\(\begin{array}{l}C + T =  – 0,016{t^4} + 0,49{t^3} – 4,8{t^2} + 14t + 70 + \left( { – 0,01{t^4} + 0,31{t^3} – 3{t^2} + 11t + 23} \right)\\ = \left( { – 0,016 – 0,01} \right){t^4} + \left( {0,49 + 0,31} \right){t^3} + \left( { – 4,8 – 3} \right){t^2} + \left( {14 + 11} \right)t + 70 + 23\\ =  – 0,026{t^4} + 0,8{t^3} – 7,8{t^2} + 25t + 93\end{array}\)

Vậy \(C + T =  – 0,026{t^4} + 0,8{t^3} – 7,8{t^2} + 25t + 93\)

Số xe được bán ra vào năm 1990 (ứng với \(t = 7\)) là

\(C + T =  – 0,{026.7^4} + 0,{8.7^3} – 7,{8.7^2} + 25.7 + 93 = 97,774\)
Vậy số xe được bán ra vào năm 1990 là 97774 chiếc.

 

–>

— *****

Giải bài 10 trang 31 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Dân số nước Mỹ từ năm 1980 tới năm 1996 được tính theo công thức:

\(P =  – 0,8{t^4} + 27{t^3} – 262{t^2} + 3010t + 227000\)

Và số người từ 85 tuổi trở lên thì tính theo công thức:

\(S = 0,02{t^4} – 0,7{t^3} + 6,4{t^2} + 213t + 7740\)

Trong đó P, S tính theo đơn vị nghìn người, t là số năm tính từ 1980. Viết biểu thức biểu thị số người Mỹ dưới 85 tuổi và tính số người đó vào năm 1995 (ứng với \(t = 15\)).

Hướng dẫn giải chi tiết Bài 10

Phương pháp giải

Thực hiện phép trừ đa thức một biến

Bước 1: Sắp xếp các đơn thức của hai đa thức cùng theo thứ tự lũy thừa giảm dần (hoặc tăng dần) của biến.

Bước 2: Thực hiện phép tính theo hàng ngang hoặc cột dọc.

Lời giải chi tiết

Biểu thức biểu thị số người Mỹ dưới 85 tuổi là

\(\begin{array}{l}P – S =  – 0,8{t^4} + 27{t^3} – 262{t^2} + 3010t + 227000 – \left( {0,02{t^4} – 0,7{t^3} + 6,4{t^2} + 213t + 7740} \right)\\ =  – 0,82{t^4} + 27,7{t^3} – 268,4{t^2} + 2797t + 219260\end{array}\)

Khi \(t = 15\) thì số người Mỹ dưới 85 tuổi là

\(P – S =  – 0,{82.15^4} + 27,{7.15^3} – 268,{4.15^2} + 2797.15 + 219260 = 252800\) người. 

 

–>

— *****