Giải SBT Bài 4: Phép nhân và phép chia đa thức một biến (C7 SBT Toán 7 Chân trời)
===========
Giải bài 1 trang 32 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST
Thực hiện phép nhân \(\left( {7x – 2} \right)\left( { – 2x + 5} \right)\).
Hướng dẫn giải chi tiết Bài 1
Phương pháp giải
Nắm rõ quy tắc nhân đa thức một biến: Muốn nhân một đa thức với một đa thức ta nhân mỗi số hạng của đa thức này với từng số hạng của đa thức kia rồi cộng các tích với nhau
Lời giải chi tiết
\(\left( {7x – 2} \right)\left( { – 2x + 5} \right) = 7x\left( { – 2x} \right) + 7x.5 + \left( { – 2} \right)\left( { – 2x} \right) + \left( { – 2} \right).5 = – 14{x^2} + 39x – 10\)
–>
— *****
Giải bài 2 trang 32 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST
Thực hiện phép nhân \(\left( {3x – 4} \right)\left( { – 2{x^2} + 7x + 4} \right)\).
Hướng dẫn giải chi tiết Bài 2
Phương pháp giải
Nắm rõ quy tắc nhân đa thức một biến: Muốn nhân một đa thức với một đa thức ta nhân mỗi số hạng của đa thức này với từng số hạng của đa thức kia rồi cộng các tích với nhau.
Lời giải chi tiết
\(\begin{array}{l}\left( {3x – 4} \right)\left( { – 2{x^2} + 7x + 4} \right)\\ = 3x\left( { – 2{x^2}} \right) + 3x.7x + 3x.4 + \left( { – 4} \right).\left( { – 2{x^2}} \right) + \left( { – 4} \right).7x + \left( { – 4} \right).4\\ = – 6{x^3} + 21{x^2} + 12x + 8{x^2} – 28x – 16\\ = – 6{x^3} + 29{x^2} – 16x – 16\end{array}\)
–>
— *****
Giải bài 3 trang 32 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST
Thực hiện phép nhân \(\left( {4{x^2} – 2x + 1} \right)\left( { – 2{x^2} + 5x + 3} \right)\).
Hướng dẫn giải chi tiết Bài 3
Phương pháp giải
Nắm rõ quy tắc nhân đa thức một biến: Muốn nhân một đa thức với một đa thức ta nhân mỗi số hạng của đa thức này với từng số hạng của đa thức kia rồi cộng các tích với nhau.
Lời giải chi tiết
\(\begin{array}{l}\left( {4{x^2} – 2x + 1} \right)\left( { – 2{x^2} + 5x + 3} \right)\\ = 4{x^2}\left( { – 2{x^2}} \right) + 4{x^2}.5x + 4{x^2}.3 – 2x.\left( { – 2{x^2}} \right) – 2x.5x – 2x.3 + \left( { – 2{x^2}} \right) + 5x + 3\\ = – 8{x^4} + 20{x^3} + 12{x^2} + 4{x^3} – 10{x^2} – 6x – 2{x^2} + 5x + 3\\ = – 8{x^4} + 24{x^3} – x + 3\end{array}\)
–>
— *****
Giải bài 4 trang 33 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST
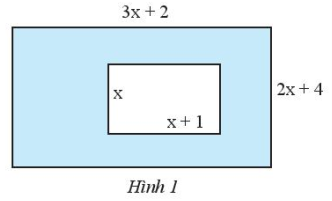
Hãy lập biểu thức có dạng đa thức theo biến \(x\) biểu thị diện tích của phần được tô đậm trong Hình 1.

Hướng dẫn giải chi tiết Bài 4
Phương pháp giải
Sử dụng các công thức tính diện tích đã học để viết được biểu thức.
Diện tích hình chữ nhật bằng tích chiều dài và chiều rộng
Lời giải chi tiết
Diện tích hình chữ nhật lớn là \(\left( {3x + 2} \right)\left( {2x + 4} \right) = 2x.3x + 2x.2 + 4.3x + 4.2 = 6{x^2} + 16x + 8\).
Diện tích hình chữ nhật nhỏ là \(x\left( {x + 1} \right) = {x^2} + x\).
Diện tích cần tìm là \(6{x^2} + 16x + 8 – \left( {{x^2} + x} \right) = 5{x^2} + 15x + 8\).
–>
— *****
Giải bài 5 trang 33 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST
Thực hiện phép chia \(\left( {9{x^5} – 15{x^4} + 27{x^3} – 12{x^2}} \right):3{x^2}\).
Hướng dẫn giải chi tiết Bài 5
Phương pháp giải
Phép chia đa thức cho đơn thức: Lấy từng hạng tử của đa thức chia cho đơn thức rồi cộng các thương với nhau.
Lời giải chi tiết
\(\begin{array}{l}\left( {9{x^5} – 15{x^4} + 27{x^3} – 12{x^2}} \right):3{x^2}\\ = 9{x^5}:3{x^2} + \left( { – 15{x^4}} \right):3{x^2} + 27{x^3}:3{x^2} + \left( { – 12{x^2}} \right):3{x^2}\\ = 3{x^3} – 5{x^2} + 9x – 4\end{array}\)
–>
— *****
Giải bài 6 trang 33 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST
Thực hiện phép chia \(\left( {2{x^2} – 5x + 3} \right):\left( {2x – 3} \right)\).
Hướng dẫn giải chi tiết Bài 6
Phương pháp giải
Chia đa thức chia đa thức bằng cách đặt phép tính chia.
Lời giải chi tiết
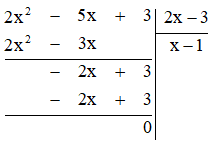
Vậy \(\left( {2{x^2} – 5x + 3} \right):\left( {2x – 3} \right) = x – 1\)
–>
— *****
Giải bài 7 trang 33 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST
Thực hiện phép chia \(\left( {4{x^2} – 5} \right):\left( {x – 2} \right)\).
Hướng dẫn giải chi tiết Bài 7
Phương pháp giải
Chia đa thức chia đa thức bằng cách đặt phép tính chia.
Lời giải chi tiết
Ta thực hiện đặt tính phép chia đa thức:
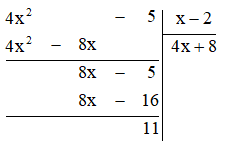
Vậy \(\frac{{4{x^2} – 5}}{{x – 2}} = 4x + 8 + \frac{{11}}{{x – 2}}\).
–>
— *****
Giải bài 8 trang 33 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST
Thực hiện phép chia \(\left( {4{x^3} – 7x + 2} \right):\left( {2{x^2} – 3} \right)\).
Hướng dẫn giải chi tiết bài 8
Phương pháp giải
Chia đa thức chia đa thức bằng cách đặt phép tính chia.
Lời giải chi tiết
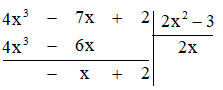
Vậy \(\frac{{4{x^3} – 7x + 2}}{{2{x^2} – 3}} = 2x + \frac{{ – x + 2}}{{2{x^2} – 3}}\)
–>
— *****
Giải bài 9 trang 33 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST
Tính chiều dài của một hình chữ nhật có diện tích bằng \(4{y^2} + 4y – 3\) (cm2) và chiều rộng bằng \(\left( {2y – 1} \right)\)(cm).
Hướng dẫn giải chi tiết Bài 9
Phương pháp giải
Chiều dài hình chữ nhật là thương của phép chia diện tích cho chiều rộng.
Lời giải chi tiết
Ta có
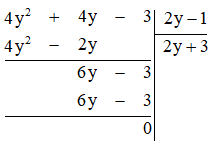
Vậy chiều dài hình chữ nhật đã cho là \(2y + 3\) cm.
–>
— *****
Giải bài 10 trang 33 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST
Cho hình hộp chữ nhật có thể tích bằng \(V = 3{x^3} + 8{x^2} – 45x – 50\) (cm3), chiều dài bằng \(\left( {x + 5} \right)\) cm và chiều cao \(\left( {x + 1} \right)\) cm. Hãy tính chiều rộng của hình hộp chữ nhật.
Hướng dẫn giải chi tiết Bài 10
Phương pháp giải
Thể tích của hình hộp chữ nhật là tích của ba kích thước.
Chiều rộng bằng thể tích chia cho tích của chiều dài và chiều cao
Lời giải chi tiết
Ta có chiều rộng được tính bởi phép tính:
\(\left( {3{x^3} + 8{x^2} – 45x – 50} \right):\left[ {\left( {x + 5} \right)\left( {x + 1} \right)} \right] = \left( {3{x^3} + 8{x^2} – 45x – 50} \right):\left( {{x^2} + 6x + 5} \right)\)
Ta có
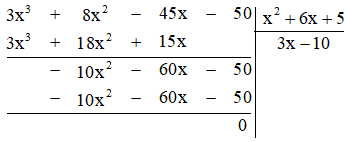
Vậy chiều rộng của hình chữ nhật là \(3x – 10\) cm.
–>
— *****
