Giải SBT Cuối chương 7 – Toán 7 SBT Chân trời

Giải SBT Cuối chương 7 – Toán 7 SBT Chân trời
==========

Giải bài 1 trang 33 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Cho \(B = x{y^3} + 4xy – 2{x^2} + 3\). Tính giá trị của biểu thức \(B\) khi \(x =  – 1\), \(y = 2\).

Hướng dẫn giải chi tiết Bài 1

Phương pháp giải

Thay các giá trị của biến và tính.

Lời giải chi tiết

Thay \(x =  – 1\), \(y = 2\) vào \(B = x{y^3} + 4xy – 2{x^2} + 3\) ta có

\(B = \left( { – 1} \right){.2^3} + 4\left( { – 1} \right).2 – 2.{\left( { – 1} \right)^2} + 3 =  – 15\).

 

–>

— *****

Giải bài 2 trang 33 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Trong các biểu thức sau, biểu thức nào là đơn thức một biến?

a) \(2y\);       

b) \(3x + 5\);      

c) \(12\);       

d) \(\frac{1}{3}{t^2}\).

Hướng dẫn giải chi tiết Bài 2

Phương pháp giải

Đơn thức một biến là biểu thức đại số chỉ gồm một số, hoặc một biến, hoặc một tích giữa các số và biến đó.

Lời giải chi tiết

Các đơn thức một biến là a; c; d.

 

–>

— *****

Giải bài 3 trang 33 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Trong các biểu thức sau, biểu thức nào là đa thức một biến?

\(5 – 2x\);          \(6{x^2} + 8{x^3} + 3x – 2\);             

\(\frac{2}{{x – 1}}\);          \(\frac{1}{4}t – 5\).

Hướng dẫn giải chi tiết Bài 3

Phương pháp giải

Nắm rõ khái niệm đơn thức một biến, đa thức một biến để xác định.

Đơn thức một biến là biểu thức đại số chỉ gồm một số, hoặc một biến, hoặc một tích giữa các số và biến đó.

Đa thức một biến là tổng của những đơn thức cùng một biến.

Lời giải chi tiết

Các đa thức một biến là “ \(5 – 2x;\,\,6{x^2} + 8{x^3} + 3x – 2\); \(\frac{1}{4}t – 5\).

 

–>

— *****

Giải bài 4 trang 33 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Hãy viết một đa thức một biến bậc bốn có 5 số hạng.

Hướng dẫn giải chi tiết Bài 4

Phương pháp giải

Đa thức một biến bậc bốn tức là bậc của biến lớn nhất là 4.

Lời giải chi tiết

Đa thức một biến bậc bốn có 5 số hạng là:

A(x) = x⁴ – 2x³ + 3x² – 4x + 5.

Nhận xét:  Bài này có nhiều cách trả lời.

 

–>

— *****

Giải bài 5 trang 33 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Hãy nêu bậc của các đa thức sau:

\(A = 5{x^2} – 2{x^4} + 7\); 

\(B = 17\);      

\(C = 3x – 4{x^3} + 2{x^2} + 1\).

Hướng dẫn giải chi tiết Bài 5

Phương pháp giải

Bậc của đa thức là số mũ lớn nhất của biến sau khi đã rút gọn đa thức.

Lời giải chi tiết

Bậc của \(A = 5{x^2} – 2{x^4} + 7\) là 2.

Bậc của \(B = 17\)là 0.

Bậc của \(C = 3x – 4{x^3} + 2{x^2} + 1\) là 3.

 

–>

— *****

Giải bài 6 trang 33 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Cho đa thức \(P\left( x \right) = {x^3} + 64\). Tìm nghiệm của đa thức trong tập hợp \(\left\{ {0;4; – 4} \right\}\)

Hướng dẫn giải chi tiết Bài 6

Phương pháp giải

Thay \(x = {x_0}\) vào \(P\left( x \right)\) nếu \(P\left( {{x_0}} \right) = 0\) thì \(x = {x_0}\) là nghiệm của \(P\left( x \right)\).

Lời giải chi tiết

Với \(x = 0\) ta có \(P\left( 0 \right) = {0^3} + 64 = 64 \ne 0\), suy ra \(0\) không là nghiệm của \(P\left( x \right)\).

Với \(x = 4\) ta có \(P\left( 4 \right) = {4^3} + 64 = 128 \ne 0\), suy ra \(4\) không là nghiệm của \(P\left( x \right)\).

Với \(x =  – 4\) ta có \(P\left( { – 4} \right) = {\left( { – 4} \right)^3} + 64 = 0\), suy ra \( – 4\) là nghiệm của \(P\left( x \right)\).

Vậy \( – 4\) là nghiệm của \(P\left( x \right)\).

 

–>

— *****

Giải bài 7 trang 33 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Tam giác có độ dài hai cạnh là \(3y + 2\); \(6y – 4\) và chu vi bằng \(23y – 5\). Tìm cạnh chưa biết trong tam giác đó.

Hướng dẫn giải chi tiết Bài 7

Phương pháp giải

Chu vi của tam giác bằng tổng ba cạnh của tam giác đó. Nên muốn tìm cạnh chưa biết ta lấy chu vi trừ đi các cạnh đã biết.

Lời giải chi tiết

Cạnh chưa biết trong tam giác đó là \(23y – 5 – \left( {3y + 2} \right) – \left( {6y – 4} \right) = 14y – 3\). 

 

–>

— *****

Giải bài 8 trang 34 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Cho đa thức \(M\left( x \right) = 3{x^5} – 4{x^3} + 9x + 2\). Tìm các đa thức \(N\left( x \right)\), \(Q\left( x \right)\) sao cho \(N\left( x \right) – M\left( x \right) =  – 5{x^4} – 4{x^3} + 2{x^2} + 8x\) và \(Q\left( x \right) + M\left( x \right) = 3{x^4} – 2{x^3} + 9{x^2} – 7\)

Hướng dẫn giải chi tiết Bài 8

Phương pháp giải

Bước 1: Thực hiện cộng trừ các đơn thức cùng một biến để rút gọn đa thức đã cho.

Bước 2: Sắp xếp các đơn thức theo lũy thừa giảm dần của biến.

Bước 3: Thực hiện phép tính theo hàng ngang hoặc cột dọc.

Lời giải chi tiết

\(N\left( x \right) – M\left( x \right) =  – 5{x^4} – 4{x^3} + 2{x^2} + 8x \Rightarrow N\left( x \right) =  – 5{x^4} – 4{x^3} + 2{x^2} + 8x + M\left( x \right)\)

\( – 5{x^4} – 4{x^3} + 2{x^2} + 8x + 3{x^5} – 4{x^3} + 9x + 2 = 3{x^5} – 5{x^4} – 8{x^3} + 2{x^2} + 17x + 2\)

Vậy \(N\left( x \right) = 3{x^5} – 5{x^4} – 8{x^3} + 2{x^2} + 17x + 2\).

\(Q\left( x \right) + M\left( x \right) = 3{x^4} – 2{x^3} + 9{x^2} – 7 \Rightarrow Q\left( x \right) = 3{x^4} – 2{x^3} + 9{x^2} – 7 – M\left( x \right)\)

\(3{x^4} – 2{x^3} + 9{x^2} – 7 – \left( {3{x^5} – 4{x^3} + 9x + 2} \right) = 3{x^4} – 2{x^3} + 9{x^2} – 7 – 3{x^5} + 4{x^3} – 9x – 2 =  – 3{x^5} + 3{x^4} + 2{x^3} + 9{x^2} – 9x – 9\) 

 

–>

— *****

Giải bài 9 trang 34 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Thực hiện phép nhân.

a) \(\left( {4x – 5} \right)\left( {3x + 4} \right)\);                         

b) \(\left( {2{x^2} – 3x + 5} \right)\left( {4x + 3} \right)\)

Hướng dẫn giải chi tiết Bài 9

Phương pháp giải

Nắm rõ quy tắc nhân đa thức một biến: Muốn nhân một đa thức với một đa thức ta nhân mỗi số hạng của đa thức này với từng số hạng của đa thức kia rồi cộng các tích với nhau.

Lời giải chi tiết

a) \(\left( {4x – 5} \right)\left( {3x + 4} \right) = 4x.3x + 4x.4 – 5.3x – 5.4 = 12{x^2} + x – 20\);                                                 

b) \(\left( {2{x^2} – 3x + 5} \right)\left( {4x + 3} \right) = 2{x^2}.4x + 2{x^2}.3 – 3x.4x – 3x.3 + 5.4x + 5.3 = 8{x^3} – 6{x^2} + 11x + 15\) 

 

–>

— *****

Giải bài 10 trang 34 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Thực hiện phép chia.

a) \(\left( {64{y^2} – 16{y^4} + 8{y^5}} \right):4y\)   

b) \(\left( {5{t^2} – 8t + 3} \right):\left( {t – 1} \right)\)

Hướng dẫn giải chi tiết Bài 10

Phương pháp giải

 

Lời giải chi tiết

 

 

–>

— *****

Giải bài 11 trang 34 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Thực hiện phép chia.

a) \(\left( {{x^4} + 6{x^2} + 8} \right):\left( {{x^2} + 2} \right)\)        

b) \(\left( {3{x^3} – 2{x^2} + 3x – 2} \right):\left( {{x^2} + 1} \right)\)

Hướng dẫn giải chi tiết Bài 11

Phương pháp giải

Chia đa thức chia đa thức bằng cách đặt phép tính chia.

Lời giải chi tiết

a) 

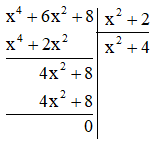
Vậy \(\left( {{x^4} + 6{x^2} + 8} \right):\left( {{x^2} + 2} \right) = {x^2} + 4\)

b)

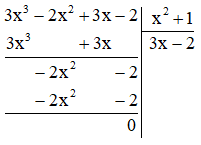
Vậy \(\left( {3{x^3} – 2{x^2} + 3x – 2} \right):\left( {{x^2} + 1} \right) = 3x – 2\).

 

–>

— *****

Giải bài 12 trang 34 SBT Toán 7 Chân trời sáng tạo tập 2 – CTST

Thực hiện phép chia.

a) \(\left( {2{x^2} – 7x + 4} \right):\left( {x – 2} \right)\)      

b) \(\left( {2{x^3} + 3{x^2} + 3x + 4} \right):\left( {{x^2} + 2} \right)\)

Hướng dẫn giải chi tiết Bài 12

Phương pháp giải

Chia đa thức chia đa thức bằng cách đặt phép tính chia.

Lời giải chi tiết

a) 

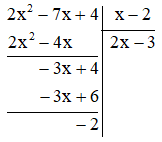
Vậy  \(\frac{{2{x^2} – 7x + 4}}{{x – 2}} = 2x – 3 – \frac{2}{{x – 2}}\).

b)

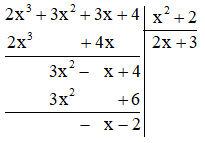
Vậy  \(\frac{{2{x^3} + 3{x^2} + 3x + 4}}{{{x^2} + 2}} = 2x + 3 – \frac{{x + 2}}{{{x^2} + 2}}\)

 

–>

— *****