Giải SBT Bài 2 Chương 9 – SBT Toán 10 CHÂN TRỜI – GIẢI CHI TIẾT
===========
Giải Bài 1 trang 65 SBT Toán 10 Chân trời sáng tạo tập 2 – CTST
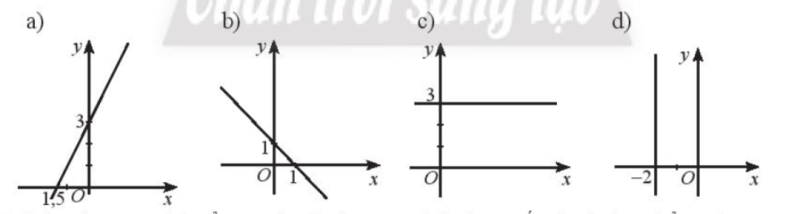
Tìm các giá trị của tham số a, b, c để phương trình \(ax + by + c = 0\) có thể biểu diễn được các đường thẳng trong hình dưới đây

Phương pháp giải
Đường thẳng \(d:ax + by + c = 0\), điểm \(A\left( {{a_0},{b_0}} \right)\) thuộc đường thẳng d khi \(a{a_0} + b{b_0} + c = 0\)
Lời giải chi tiết
a) \(\left\{ \begin{array}{l}\left( {0;3} \right) \in d\\\left( { – 1,5;0} \right) \in d\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a.0 + b.3 + c = 0\\a\left( { – 1,5} \right) + b.0 + c = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}3b + c = 0\\\left( { – 1,5} \right)a + c = 0\end{array} \right.\)
Chọn \(c = 3 \Rightarrow a = 2,b = – 1\)
Phương trình đường thẳng là \(2x – y + 3 = 0\)
b) \(\left\{ \begin{array}{l}\left( {0;1} \right) \in d\\\left( {1;0} \right) \in d\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a.0 + b.1 + c = 0\\a.1 + b.0 + c = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}b + c = 0\\a + c = 0\end{array} \right.\)
Cho \(c = – 1 \Rightarrow a = 1,b = 1\)
Phương trình đường thẳng là \(x + y – 1 = 0\)
c) \(\left\{ \begin{array}{l}\left( {0;3} \right) \in d\\\left( {1;3} \right) \in d\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a.0 + b.3 + c = 0\\a.1 + b.3 + c = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}3b + c = 0\\a + 3b + c = 0\end{array} \right.\)
Cho \(c = – 3 \Rightarrow a = 0,b = 1\)
Phương trình đường thẳng là \(y – 3 = 0\)
d) \(\left\{ \begin{array}{l}\left( { – 2;1} \right) \in d\\\left( { – 2;0} \right) \in d\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a.\left( { – 2} \right) + b.1 + c = 0\\a\left( { – 2} \right) + b.0 + c = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l} – 2a + b + c = 0\\ – 2a + c = 0\end{array} \right.\)
Cho \(c = 2 \Rightarrow a = 1,b = 0\)
Phương trình đường thẳng là \(x + 2 = 0\)
GIẢI SBT Toán 10 Chân trời sáng tạo Chương 9 Bài 2
Giải Bài 2 trang 65 SBT Toán 10 Chân trời sáng tạo tập 2 – CTST
Lập phương trình tổng quát và phương trình tham số của đường thẳng d trong mỗi trường hợp sau:
a) d đi qua điểm \(M\left( {2;2} \right)\) và vectơ chỉ phương \(\overrightarrow u = \left( {4;7} \right)\)
b) d đi qua điểm \(N\left( {0;1} \right)\) và có vectơ pháp tuyến là \(\overrightarrow n = \left( { – 5;3} \right)\)
c) d đi qua \(A\left( { – 2; – 3} \right)\) và có hệ số góc \(k = 3\)
d) d đi qua hai điểm \(P\left( {1;1} \right),Q\left( {3;4} \right)\)
Phương pháp giải
+ Phương trình tổng quát đường thẳng đi qua \(M\left( {{x_1},{y_1}} \right)\) nhận \(\overrightarrow {{a_1}} = \left( {a;b} \right)\) là vectơ pháp tuyến là: \(a\left( {x – {x_1}} \right) + b\left( {y – {y_1}} \right) = 0\)
+ Phương trình nhận \(\overrightarrow {{a_2}} = \left( {c;d} \right)\) là vectơ chỉ phương → \(\overrightarrow {{a_3}} = \left( {d; – c} \right)\)là vectơ pháp tuyến của đường thẳng đó
Lời giải chi tiết
a)
+ Phương trình tham số: \(d:\left\{ \begin{array}{l}x = 2 + 4t\\y = 2 + 7t\end{array} \right.\)
+ \(\overrightarrow u = \left( {4;7} \right) \Rightarrow \overrightarrow n = \left( {7; – 4} \right) \Rightarrow d:7\left( {x – 2} \right) – 4\left( {y – 2} \right) = 0 \Rightarrow 7x – 4y – 6 = 0\)
b)
+ Phương trình tổng quát: \(d: – 5\left( {x – 0} \right) + 3\left( {y – 1} \right) = 0 \Rightarrow d: – 5x + 3y – 3 = 0\)
+ \(\overrightarrow n = \left( { – 5;3} \right) \Rightarrow \overrightarrow v = \left( {3;5} \right) \Rightarrow d:\left\{ \begin{array}{l}x = 3t\\y = 1 + 5t\end{array} \right.\)
c)
+ Phương trình tổng quát: \(y = 3\left( {x + 2} \right) – 3 \Rightarrow d:y = 3x + 3\)
+ \(\overrightarrow n = \left( {3; – 1} \right) \Rightarrow \overrightarrow v = \left( {1;3} \right) \Rightarrow d:\left\{ \begin{array}{l}x = – 2 + t\\y = – 3 + 3t\end{array} \right.\)
d)
+ \(\overrightarrow {PQ} = \left( {2;3} \right) \Rightarrow d:\left\{ \begin{array}{l}x = 1 + 2t\\y = 1 + 3t\end{array} \right.\)
+ \(\overrightarrow {PQ} = \left( {2;3} \right) \Rightarrow \overrightarrow n = \left( {3; – 2} \right) \Rightarrow d:3\left( {x – 1} \right) – 2\left( {y – 1} \right) = 0 \Rightarrow 3x – 2y – 1 = 0\)
GIẢI SBT Toán 10 Chân trời sáng tạo Chương 9 Bài 2
Giải Bài 3 trang 66 SBT Toán 10 Chân trời sáng tạo tập 2 – CTST
Cho tam giác ABC, biết \(A\left( {1;4} \right),B\left( {0;1} \right),C\left( {4;3} \right)\)
a) Lập phương trình tổng quát của đường thẳng BC
b) Lập phương trình tham số của đường trung tuyến AM
c) Lập phương trình tổng quát của đường cao AH
Phương pháp giải
Phương trình tổng quát đường thẳng đi qua \(M\left( {{x_1},{y_1}} \right)\) nhận \(\overrightarrow {{a_1}} = \left( {a;b} \right)\) là vectơ pháp tuyến là: \(a\left( {x – {x_1}} \right) + b\left( {y – {y_1}} \right) = 0\)
Lời giải chi tiết
Ta có \(A\left( {1;4} \right),B\left( {0;1} \right),C\left( {4;3} \right)\)
a) \(\overrightarrow {BC} = \left( {4;2} \right) \Rightarrow \overrightarrow n = \left( {1; – 2} \right) \Rightarrow BC:1\left( {x – 0} \right) – 2\left( {y – 1} \right) = 0 \Rightarrow x – 2y + 2 = 0\)
b) M là trung điểm của BC → \(\begin{array}{l}M\left( {2;2} \right) \Rightarrow \overrightarrow {AM} = \left( {1; – 2} \right)\\ \Rightarrow AM:\left\{ \begin{array}{l}x = 1 + t\\y = 4 – 2t\end{array} \right.\end{array}\)
c) \(\overrightarrow {AH} \bot \overrightarrow {BC} \Rightarrow \overrightarrow {{n_{AH}}} = \overrightarrow {BC} = \left( {2;1} \right)\)
\( \Rightarrow AH:2\left( {x – 1} \right) + 1\left( {y – 4} \right) = 0 \Rightarrow AH:2x + y – 6 = 0\)
GIẢI SBT Toán 10 Chân trời sáng tạo Chương 9 Bài 2
Giải Bài 4 trang 66 SBT Toán 10 Chân trời sáng tạo tập 2 – CTST
Lập phương trình tổng quát của đường thẳng \(\Delta \) trong mỗi trường hợp sau:
a) \(\Delta \) đi qua \(M\left( {3;3} \right)\) và song song với đường thẳng \(x + 2y – 2022 = 0\)
b) \(\Delta \) đi qua \(N\left( {2; – 1} \right)\) và vuông góc với đường thẳng \(3x + 2y + 99 = 0\)
Phương pháp giải
Trong mặt phẳng toạ độ, mọi đường thẳng đều có phương trình tổng quát dạng ax + by + c =0, với a và b không đồng thời bằng 0. Ngược lại, mỗi phương trình dạng ax + by + c =0, với a và b không đồng thời bằng 0, đều là phương trình của một đường thẳng, nhận \(\overrightarrow n \left( {a;b} \right)\) là một vectơ pháp tuyến.
Lời giải chi tiết
a)
+ \(\Delta \) song song với đường thẳng \(x + 2y – 2022 = 0\) → \(\Delta 😡 + 2y + c = 0\left( {c \ne – 2022} \right)\)
+ \(\Delta \) đi qua \(M\left( {3;3} \right)\) → \(3 + 2.3 + c = 0 \Rightarrow c = – 9 \Rightarrow \Delta 😡 + 2y – 9 = 0\)
b)
+ \(\Delta \) vuông góc với đường thẳng \(3x + 2y + 99 = 0 \Rightarrow \Delta :2x – 3y + c = 0\)
+ \(\Delta \) đi qua \(N\left( {2; – 1} \right)\) → \(2.2 – 3\left( { – 1} \right) + c = 0 \Rightarrow c = – 7 \Rightarrow \Delta :2x – 3y – 7 = 0\)
GIẢI SBT Toán 10 Chân trời sáng tạo Chương 9 Bài 2
Giải Bài 5 trang 66 SBT Toán 10 Chân trời sáng tạo tập 2 – CTST
Xét vị trí tương đối của các cặp đường thẳng \({d_1}\) và \({d_2}\) sau đây:
a) \({d_1}:2x + y + 9 = 0\) và \({d_2}:2x + 3y – 9 = 0\)
b) \({d_1}:\left\{ \begin{array}{l}x = 2 + t\\y = 1 – 2t\end{array} \right.\) và \({d_2}:2x + y + 10 = 0\)
c) \({d_1}:\left\{ \begin{array}{l}x = 1 – t\\y = 8 – 5t\end{array} \right.\) và \({d_2}:5x – y + 3 = 0\)
Phương pháp giải
\({\Delta _1}\) cắt \({\Delta _2}\) tại \(M\left( {{x_0};{y_0}} \right)\) ⇔ hệ (*) có nghiệm duy nhất \(\left( {{x_0};{y_0}} \right)\).
\({\Delta _1}\) song song với \({\Delta _2}\) ⇔ hệ (*) vô nghiệm.
\({\Delta _1}\) trùng \({\Delta _2}\) ⇔ hệ (*) có vô số nghiệm.
Lời giải chi tiết
a) Vectơ pháp tuyến của \({d_1}\) và \({d_2}\) lần lượt là \(\overrightarrow {{n_1}} = \left( {2;1} \right),\overrightarrow {{n_2}} = \left( {2;3} \right)\)→ Hai đường thẳng cắt nhau
b) Vectơ pháp tuyến của \({d_1}\) và \({d_2}\) lần lượt là: \(\overrightarrow {{n_1}} = \left( {2;1} \right),\overrightarrow {{n_2}} = \left( {2;1} \right)\)
Ta thấy \(\overrightarrow {{n_2}} = \overrightarrow {{n_1}} \) → Hai đường thẳng song song hoặc trùng nhau
Xét \(A\left( {2;1} \right)\) thuộc \({d_1}\), ta thấy A không thuộc \({d_2}\) → Hai đường thẳng này song song với nhau
c) Vectơ pháp tuyến của \({d_1}\) và \({d_2}\) lần lượt là: \(\overrightarrow {{n_1}} = \left( {5; – 1} \right),\overrightarrow {{n_2}} = \left( {5; – 1} \right)\)
Ta thấy \(\overrightarrow {{n_2}} = \overrightarrow {{n_1}} \) → Hai đường thẳng song song hoặc trùng nhau
Xét \(A\left( {1;8} \right)\) thuộc \({d_1}\), ta thấy A cũng thuộc \({d_2}\) → Hai đường thẳng này trùng nhau
GIẢI SBT Toán 10 Chân trời sáng tạo Chương 9 Bài 2
Giải Bài 6 trang 66 SBT Toán 10 Chân trời sáng tạo tập 2 – CTST
Cho đường thẳng d có phương trình tham số \(\left\{ \begin{array}{l}x = 1 + t\\y = 2 + 2t\end{array} \right.\)
Tìm giao điểm của d với đường thẳng \(\Delta 😡 + y – 2 = 0\)
Phương pháp giải
\({\Delta _1}\) cắt \({\Delta _2}\) tại \(M\left( {{x_0};{y_0}} \right)\) ⇔ hệ (*) có nghiệm duy nhất \(\left( {{x_0};{y_0}} \right)\).
\({\Delta _1}\) song song với \({\Delta _2}\) ⇔ hệ (*) vô nghiệm.
\({\Delta _1}\) trùng \({\Delta _2}\) ⇔ hệ (*) có vô số nghiệm.
Lời giải chi tiết
Gọi \(A\left( {{x_A};{y_A}} \right)\) là giao điểm của 2 đường thẳng.
\( \Rightarrow A \in d\) và \(A \in \Delta \)
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{{x_A} = 1 + t}\\
{{y_A} = 2 + 2t}
\end{array}} \right.\) và \({x_A} + {y_A} – 2 = 0\)
\( \Rightarrow (1 + t) + (2 + 2t) – 2 = 0 \Rightarrow 3t + 1 = 0 \Rightarrow t = \frac{{ – 1}}{3}\)
\( \Rightarrow {x_A} = \frac{2}{3};{y_A} = \frac{4}{3}\)
Vậy giao của hai đường thẳng là \( A\left( {\frac{2}{3};\frac{4}{3}} \right)\)
GIẢI SBT Toán 10 Chân trời sáng tạo Chương 9 Bài 2
Giải Bài 7 trang 66 SBT Toán 10 Chân trời sáng tạo tập 2 – CTST
Tìm số đo của góc giữa hai đường thẳng \({d_1}\) và \({d_2}\) trong các trường hợp sau:
a) \({d_1}:5x – 3y + 1 = 0\) và \({d_2}:10x – 6y – 7 = 0\)
b) \({d_1}:7x – 3y + 7 = 0\) và \({d_2}:3x + 7y – 10 = 0\)
c) \({d_1}:2x – 4y + 9 = 0\) và \({d_2}:6x – 2y – 2023 = 0\)
Phương pháp giải
\(\left( {a;b} \right)\) và \(\left( {c;d} \right)\) cùng là vectơ pháp tuyến hoặc chỉ phương của hai đường thẳng \({d_1}\) và \({d_2}\).
Góc giữa hai đường thẳng là \(\varphi \), thì \(cos\varphi = \frac{{\left| {ac + bd} \rig
Lời giải chi tiết
a) Vectơ pháp tuyến của hai đường thẳng lần lượt là \(\left( {5; – 3} \right)\) và \(\left( {10; – 6} \right) = 2\left( {5; – 3} \right)\)
=> Hai vecto pháp tuyến cùng phương.
→ Hai đường thẳng song song với nhau\( \Rightarrow \varphi = {0^ \circ }\)
b) Vectơ pháp tuyến của hai đường thẳng lần lượt là \(\left( {7; – 3} \right)\) và \(\left( {3;7} \right)\).
Ta có: \(\left( {7; – 3} \right).\left( {3;7} \right) = 0\)
\(\Rightarrow \) Hai đường thẳng vuông góc với nhau \( \Rightarrow \varphi = {90^ \circ }\)
c) Vectơ pháp tuyến của hai đường thẳng lần lượt là \(\left( {2; – 4} \right)\) và \(\left( {6; – 2} \right)\).
\(cos\varphi = \frac{{\left| {2.6 + \left( { – 4} \right).\left( { – 2} \right)} \right|}}{{\sqrt {{2^2} + {{\left( { – 4} \right)}^2}} \sqrt {{6^2} + {{\left( { – 2} \right)}^2}} }} = \frac{1}{{\sqrt 2 }} \Rightarrow \varphi = {45^ \circ }\)
GIẢI SBT Toán 10 Chân trời sáng tạo Chương 9 Bài 2
Giải Bài 7 trang 66 SBT Toán 10 Chân trời sáng tạo tập 2 – CTST
Tìm số đo của góc giữa hai đường thẳng \({d_1}\) và \({d_2}\) trong các trường hợp sau:
a) \({d_1}:5x – 3y + 1 = 0\) và \({d_2}:10x – 6y – 7 = 0\)
b) \({d_1}:7x – 3y + 7 = 0\) và \({d_2}:3x + 7y – 10 = 0\)
c) \({d_1}:2x – 4y + 9 = 0\) và \({d_2}:6x – 2y – 2023 = 0\)
Phương pháp giải
\(\left( {a;b} \right)\) và \(\left( {c;d} \right)\) cùng là vectơ pháp tuyến hoặc chỉ phương của hai đường thẳng \({d_1}\) và \({d_2}\).
Góc giữa hai đường thẳng là \(\varphi \), thì \(cos\varphi = \frac{{\left| {ac + bd} \rig
Lời giải chi tiết
a) Vectơ pháp tuyến của hai đường thẳng lần lượt là \(\left( {5; – 3} \right)\) và \(\left( {10; – 6} \right) = 2\left( {5; – 3} \right)\)
=> Hai vecto pháp tuyến cùng phương.
→ Hai đường thẳng song song với nhau\( \Rightarrow \varphi = {0^ \circ }\)
b) Vectơ pháp tuyến của hai đường thẳng lần lượt là \(\left( {7; – 3} \right)\) và \(\left( {3;7} \right)\).
Ta có: \(\left( {7; – 3} \right).\left( {3;7} \right) = 0\)
\(\Rightarrow \) Hai đường thẳng vuông góc với nhau \( \Rightarrow \varphi = {90^ \circ }\)
c) Vectơ pháp tuyến của hai đường thẳng lần lượt là \(\left( {2; – 4} \right)\) và \(\left( {6; – 2} \right)\).
\(cos\varphi = \frac{{\left| {2.6 + \left( { – 4} \right).\left( { – 2} \right)} \right|}}{{\sqrt {{2^2} + {{\left( { – 4} \right)}^2}} \sqrt {{6^2} + {{\left( { – 2} \right)}^2}} }} = \frac{1}{{\sqrt 2 }} \Rightarrow \varphi = {45^ \circ }\)
GIẢI SBT Toán 10 Chân trời sáng tạo Chương 9 Bài 2
Giải Bài 8 trang 66 SBT Toán 10 Chân trời sáng tạo tập 2 – CTST
Tính khoảng cách từ điểm M đến đường thẳng \(\Delta \) trong các trường hợp sau:
a) \(M\left( {2;3} \right)\) và \(\Delta :8x – 6y + 7 = 0\)
b) \(M\left( {0;1} \right)\) và \(\Delta :4x + 9y – 20 = 0\)
c) \(M\left( {1;1} \right)\) và \(\Delta :3y – 5 = 0\)
d) \(M\left( {4;9} \right)\) và \(\Delta 😡 – 25 = 0\)
Phương pháp giải
Khoảng cách từ 1 điểm \(A\left( {{x_0};{y_0}} \right)\) đến đường thẳng \(d:ax + by + c = 0\) là:
\(d\left( {A,d} \right) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)
Lời giải chi tiết
a) \(d\left( {M,\Delta } \right) = \frac{{\left| {8.2 – 6.3 + 7} \right|}}{{\sqrt {{8^2} + {{\left( { – 6} \right)}^2}} }} = \frac{1}{2}\)
b) \(d\left( {M,\Delta } \right) = \frac{{\left| {4.0 + 9.1 – 20} \right|}}{{\sqrt {{4^2} + {9^2}} }} = \frac{{11}}{{\sqrt {97} }}\)
c) \(d\left( {M,\Delta } \right) = \frac{{\left| {3.1 – 5} \right|}}{{\sqrt {{0^2} + {3^2}} }} = \frac{2}{3}\)
d) \(d\left( {M,\Delta } \right) = \frac{{\left| {4 – 25} \right|}}{{\sqrt {{1^2} + {0^2}} }} = 21\)
GIẢI SBT Toán 10 Chân trời sáng tạo Chương 9 Bài 2
Giải Bài 9 trang 66 SBT Toán 10 Chân trời sáng tạo tập 2 – CTST
Tìm c để đường thẳng \(\Delta :4x – 3y + c = 0\) tiếp xúc với đường tròn \(\left( C \right)\) có \(J\left( {1;2} \right)\) và bán kính \(R = 3\)
Phương pháp giải
\(\Delta\) tiếp xúc với đường tròn \(\left( C \right)\) tâm J
Lời giải chi tiết
\(d\left( {J,\Delta } \right) = R\)
\( \Leftrightarrow \frac{{\left| {4.1 – 3.2 + c} \right|}}{{\sqrt {{4^2} + {3^2}} }} = 3 \Leftrightarrow \frac{{\left| {c – 2} \right|}}{5} = 3 \Leftrightarrow\left| {c – 2} \right| = 15 \Leftrightarrow \left[ \begin{array}{l}c = 17\\c = – 13\end{array} \right.\)
Vậy \(c=17\) hoặc \(c=-13\) thì \(\Delta\) tiếp xúc với \(\left( C \right)\).
GIẢI SBT Toán 10 Chân trời sáng tạo Chương 9 Bài 2
Giải Bài 10 trang 66 SBT Toán 10 Chân trời sáng tạo tập 2 – CTST
Tính khoảng cách giữa hai đường thẳng: \(\Delta :6x + 8y – 11 = 0\) và \(\Delta ‘:6x + 8y – 1 = 0\)
Phương pháp giải
Khoảng cách giữa hai đường thẳng song song \(d:ax + by + c = 0\) và \(d’:ax + by + c’ = 0\) là \(d\left( {d,d’} \right) = \frac{{\left| {c – c’} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)
Lời giải chi tiết
Ta thấy \(\Delta \) và \(\Delta ‘\) song song với nhau do có cùng VTPT \(\overrightarrow n = (6;8)\)
\( \Rightarrow \) Khoảng cách giữa hai đường thẳng là:
\(d\left( {\Delta ,\Delta ‘} \right) = \frac{{\left| { – 11 – \left( { – 1} \right)} \right|}}{{\sqrt {{6^2} + {8^2}} }} = 1\)
GIẢI SBT Toán 10 Chân trời sáng tạo Chương 9 Bài 2
Giải Bài 11 trang 66 SBT Toán 10 Chân trời sáng tạo tập 2 – CTST
Một trạm viễn thông \(S\) có tọa độ \(\left( {5;1} \right)\). Một người đang ngồi trên chiếc xe khách chạy trên đoạn cao tốc có dạng một đường thẳng \(\Delta \) có phương trình \(12x + 5y – 20 = 0\). Tính khoảng cách ngắn nhất giữa người đó và trạm viễn thông \(S\). Biết rằng mỗi đơn vị độ dài tương ứng với 1 km.
Phương pháp giải
Khoảng cách từ 1 điểm \(A\left( {{x_0};{y_0}} \right)\) đến đường thẳng \(d:ax + by + c = 0\) là:
\(d\left( {A,d} \right) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)
Lời giải chi tiết
Khoảng cách ngắn nhất giữa người đó và trạm viễn thông S là đường vuông góc (hay khoảng cách) từ S đến đường thẳng \(\Delta \)
\( \Rightarrow d\left( {S,\Delta } \right) = \frac{{\left| {12.5 + 5.1 – 20} \right|}}{{\sqrt {{{12}^2} + {5^2}} }} = \frac{{45}}{{13}} \approx 3,46\)
Vậy khoảng cách ngắn nhất giữa người đó và trạm viễn thông S là 3,46 km.
GIẢI SBT Toán 10 Chân trời sáng tạo Chương 9 Bài 2
===========
THUỘC: Giải sách bài tập Toán 10 – Chân trời
