Giải bài tập Bài 8: Tính chất ba đường cao của tam giác (C8 Toán 7 Chân trời)
=============
Giải bài 1 trang 78 SGK Toán 7 Chân trời sáng tạo tập 2 – CTST
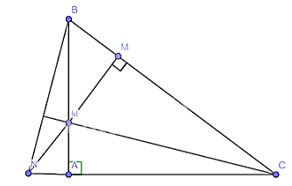
Cho tam giác ABC vuông tại A. Lấy điểm H thuộc cạnh AB. Vẽ HM vuông góc với BC tại M. Tia MH cắt tia CA tại N. Chứng minh rằng CH vuông góc với NB.
Hướng dẫn giải chi tiết Bài 1
Phương pháp giải
Ta chứng minh H là trực tâm của tam giác NBC
Lời giải chi tiết

Vì tam giác ABC vuông tại A theo giả thiết nên BA vuông góc với AC
Vì HM cắt AC tại N mà HM vuông góc với BC (giả thiết)
\( \Rightarrow \) NM vuông góc với BC tại M
Xét tam giác NBC có NM và BA là 2 đường cao
Mà MN cắt AB tại H nên H là trực tâm của tam giác NBC
\( \Rightarrow \) CH đường cao của tam giác NBC (3 đường cao của tam giác đi qua 1 điểm)
\( \Rightarrow \) CH vuông góc với NB
–>
— *****
Giải bài 2 trang 78 SGK Toán 7 Chân trời sáng tạo tập 2 – CTST
Cho tam giác ABC vuông tại A. Trên tia BA lấy điểm M sao cho BM = BC. Tia phân giác của góc B cắt AC tại H. Chứng minh rằng MH vuông góc với BC.
Hướng dẫn giải chi tiết Bài 2
Phương pháp giải
– Ta chứng minh H là trực tâm của tam giác AMC
– Từ đó ta chứng minh MH vuông góc với BC
Lời giải chi tiết
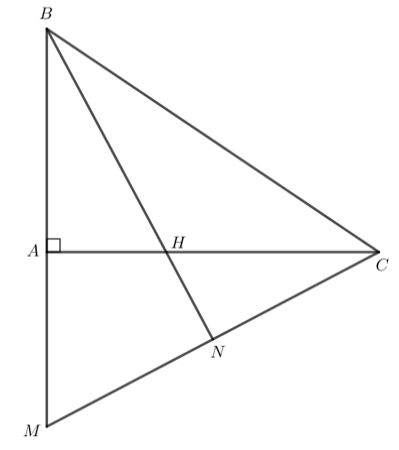
Tam giác BMC có BM = BC nên tam giác BMC cân tại B.
Tam giác BMC cân tại B, có BN là đường phân giác nên BN cũng là đường cao của tam giác BMC.
Do đó BNMC.
Tam giác BMC có CABM, BNMC nên CA, BN là hai đường cao của tam giác BMC.
Mà CA và BN cắt nhau tại H nên H là trực tâm của tam giác BMC.
Do đó MHBC.
–>
— *****
Giải bài 3 trang 78 SGK Toán 7 Chân trời sáng tạo tập 2 – CTST
Cho tam giác ABC vuông cân tại A. Lấy điểm E thuộc cạnh AC. Trên tia đối của tia AB lấy điểm D sao cho AD = AE. Chứng minh rằng:
a) DE vuông góc với BC
b) BE vuông góc với DC
Hướng dẫn giải chi tiết Bài 3
Phương pháp giải
– Ta chứng minh vuông góc qua các tam giác vuông cân
– Ta chứng minh E là trực tâm của tam giác BCD
– Từ đó ta chứng minh DE vuông góc với BC và BE vuông góc DC
Lời giải chi tiết
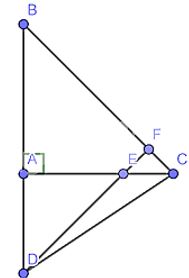
a) Vì tam giác ABC vuông cân tại A
\( \Rightarrow \) \(\widehat B = \widehat C = {45^o}\)(2 góc ở đáy bằng nhau)
Xét tam giác AED có :
AE = AD
AC vuông góc với AB
\( \Rightarrow \) Tam giác AED vuông cân tại A
\( \Rightarrow \widehat {ADE} = \widehat {AED} = {45^o}\)
Mà \(\widehat {AED};\widehat {CEF}\)là 2 góc đối đỉnh \( \Rightarrow \widehat {AED} = \widehat {CEF} = {45^o}\)
Xét tam giác CEF áp dụng định lí tổng 3 góc trong tam giác ta có :
\( \Rightarrow \widehat F + \widehat C + \widehat E = {180^o}\)
\( \Rightarrow \widehat F = {180^o} – {45^o} – {45^o} = {90^o} \Rightarrow EF \bot BC \Rightarrow DE \bot BC\)
b) Vì DE vuông góc với BC \( \Rightarrow \) DE là đường cao của tam giác BCD
Vì AC cắt DE tại E nên E là trực tâm tam giác BCD (Do AC cũng là đường cao của tam giác BCD)
\( \Rightarrow \)BE cùng là đường cao của tam giác BCD (định lí 3 đường cao trong tam giác đi qua trực tâm)
\( \Rightarrow \)BE vuông góc với DC
–>
— *****
Giải bài 4 trang 78 SGK Toán 7 Chân trời sáng tạo tập 2 – CTST
Cho tam giác nhọn ABC có ba đường cao AB, BE, CF. Biết AD = BE = CF. Chứng minh rằng tam giác ABC đều.
Hướng dẫn giải chi tiết Bài 4
Phương pháp giải
– Ta chứng tam giác BFC = tam giác BEC
– Từ đó suy ra góc B = góc C
– Chứng minh tương tự suy ra được góc A = góc B = góc C
Lời giải chi tiết
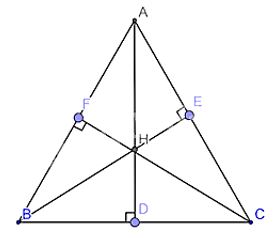
Xét tam giác BFC và tam giác BEC có :
BC chung
FC = BE
\(\widehat {BFC} = \widehat {BEC} = {90^o}\)
( cạnh huyền – cạnh góc vuông)
\( \Rightarrow \widehat C = \widehat B\) ( 2 góc tương ứng ) (1)
Xét tam giác CFA và tam giác ADC ta có :
CF = AD
AC chung
\(\widehat {ADC} = \widehat {AFC} = {90^o}\)
(cạnh huyền – cạnh góc vuông)
\( \Rightarrow \widehat C = \widehat A\)(2 góc tương ứng ) (2)
Từ (1) và (2) \( \Rightarrow \widehat C = \widehat A = \widehat B\) \( \Rightarrow \)Tam giác ABC là tam giác đều do có 3 góc bằng nhau
–>
— *****
