Giải bài tập Bài 5: Đường trung trực của một đoạn thẳng (C8 Toán 7 Chân trời)
===========
Giải bài 1 trang 70 SGK Toán 7 Chân trời sáng tạo tập 2 – CTST
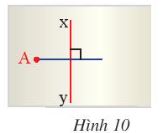
Hình 10 minh họa một tờ giấy có hình vẽ đường trung trực xy của đoạn thẳng AB mà hình ảnh điểm B bị nhòe mất. Hãy nêu cách xác định điểm B.

Hướng dẫn giải chi tiết Bài 1
Phương pháp giải
– Ta tìm giao điểm của trung trực và đoạn thẳng AB
– Rồi từ điểm đó tìm điểm B sao cho khoảng cách từ điểm đó đên A bằng B và B, A và giao điểm phải thẳng hàng, B không trùng với A
Lời giải chi tiết
Gọi giao điểm của AB và xy là O
\( \Rightarrow \) O là trung điểm AB ( Do xy là đường trung trực của AB)
\( \Rightarrow \) Đo khoảng cách AO và từ điểm O kẻ OB sao cho OA = OB và nằm khác phía với điểm A so với đường thẳng xy ( A, B, O thẳng hàng )
–>
— *****
Giải bài 2 trang 70 SGK Toán 7 Chân trời sáng tạo tập 2 – CTST
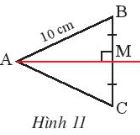
Quan sát Hình 11, cho biết M là trung điểm của BC, AM vuông góc với BC và AB = 10 cm, Tính AC.
Hướng dẫn giải chi tiết Bài 2
Phương pháp giải
Ta chứng minh 2 tam giác AMC và AMB bằng nhau
Lời giải chi tiết
Xét tam giác AMB và tam giác AMC có :
AM cạnh chung
MB = MC ( do M là trung điểm BC )
\(\widehat {BMA} = \widehat {CMA} = {90^o}\)
\( \Rightarrow \) Tam giác AMB = tam giác AMC (c-g-c)
\( \Rightarrow \)AB = AC = 10 cm ( cạnh tương ứng bằng nhau)
–>
— *****
Giải bài 3 trang 70 SGK Toán 7 Chân trời sáng tạo tập 2 – CTST
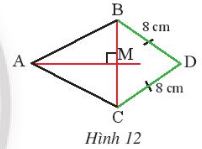
Quan sát Hình 12, cho biết AM là đường trung trực của đoạn thẳng BC và DB = DC = 8 cm. Chứng minh rằng ba điểm A, M, D thẳng hàng.
Hướng dẫn giải chi tiết Bài 3
Phương pháp giải
Chứng minh D thuộc trung trực của BC \( \Rightarrow \) A, M, D thẳng hàng
Lời giải chi tiết
Xét tam giác BCD có BD = CD ( giả thiết )
\( \Rightarrow \) D thuộc trung trực BC do cách đều 2 đầu mút đoạn BC
Mà AM là trung trực của BC
\( \Rightarrow \) D thuộc đường thẳng AM
\( \Rightarrow \) A, M, D thẳng hàng
–>
— *****
Giải bài 4 trang 70 SGK Toán 7 Chân trời sáng tạo tập 2 – CTST
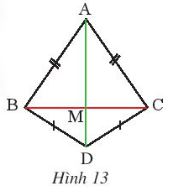
Quan sát Hình 13, biết AB = AC, DB = DC. Chứng minh rằng M là trung điểm của BC.
Hướng dẫn giải chi tiết Bài 4
Phương pháp giải
– Ta chứng minh 2 tam giác ABD và ACD bằng nhau
– Suy ra 2 tam giác BAM và CAM bằng nhau \( \Rightarrow \) BM = CM
Lời giải chi tiết
Xét tam giác ABD và tam giác ACD có :
AB = AC ( giả thiết )
BD = CD ( giả thiết )
AD cạnh chung
\( \Rightarrow \Delta ABD =\Delta ACD (c-c-c)\)
\( \Rightarrow \)\(\widehat {BAD} = \widehat {CAD}\)( 2 góc tương ứng )
Xét tam giác ABM và ta giác ACM có :
AB = AC ( giả thiết )
AM cạnh chung
\(\widehat {BAD} = \widehat {CAD}\)( chứng minh trên )
\(\Delta ABM=\Delta ACM (c-g-c)\)
\(\Rightarrow MC = MB\) ( 2 cạnh tương ứng )
\( \Rightarrow \) M là trung điểm BC
–>
— *****
Giải bài 5 trang 70 SGK Toán 7 Chân trời sáng tạo tập 2 – CTST
Cho hai điểm M và N nằm trên đường trung trực d của đoạn thẳng EF. Chứng minh rẳng \(\Delta EMN=\Delta FMN\)
Hướng dẫn giải chi tiết Bài 5
Phương pháp giải
Chứng minh 2 tam giác bằng nhau theo trường hợp (c-c-c)
Lời giải chi tiết
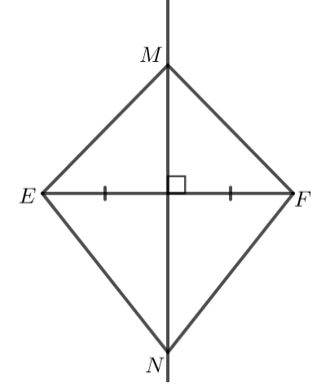
Vì M thuộc trung trực EF nên ME = MF ( tính chất điểm thuộc trung trực )
Tương tự \( \Rightarrow \) NE = NF ( tính chất điểm thuộc trung trực )
Xét 2 tam giác MEN và MFN có :
MN là cạnh chung
ME = MF
NE = NF
\(\Rightarrow \Delta MEN = \Delta MFN (c-c-c)\)
–>
— *****
Giải bài 6 trang 70 SGK Toán 7 Chân trời sáng tạo tập 2 – CTST
Trên bản đồ qui hoạch một khu dân cư có một con đường d và hai điểm dân cư A và B (Hình 14). Hãy tìm bên đường một địa điểm M để xây dựng một trạm y tế sao cho trạm y tế cách đều hai điểm dân cư.
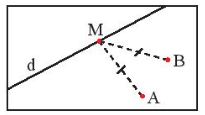
Hướng dẫn giải chi tiết Bài 6
Phương pháp giải
– Để MA = MB \( \Rightarrow \) M thuộc trung trực AB
– Tìm M thuộc d
Lời giải chi tiết
Để M cách đều A, B khi và chỉ khi M thuộc trung trực của đoạn AB
Vì M phải thuộc d \( \Rightarrow \) M là giao điểm của trung trực AB và đường thẳng d
–>
— *****
