Giải bài tập Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác (C4 Toán 7 Kết nối)

Giải bài tập Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác (C4 Toán 7 Kết nối)

————————-

Giải bài 4.4 trang 67 SGK Toán 7 KNTT tập 1

Cho tam giác ABC và DEF như hình 4.18. Trong các khẳng định sau, khẳng định nào đúng?

(1)(Delta ABC = Delta DEF)

(2) (Delta ACB = Delta EDF)

(3) (Delta BAC = Delta DFE)

(4)(Delta CAB = Delta DEF)

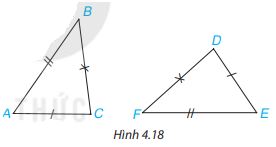
Phương pháp giải

Quan sát hình vẽ chỉ ra các cặp cạnh bằng nhau từ đó suy ra thứ tự đỉnh của hai tam giác bằng nhau.

Lời giải chi tiết

Xét tam giác (Delta ACB) và (Delta EDF) có:

(begin{array}{l}AC = ED\AB = EF\CB = DFend{array})

(Rightarrow Delta ACB = Delta EDF)(c.c.c)

Xét tam giác (Delta CAB) và (Delta DEF) có:

(begin{array}{l}CA = DE\AB = EF\CB = DFend{array})

(Rightarrow Delta CAB = Delta DEF)(c.c.c)

Vậy khẳng định (2) và (4) đúng.

Chú ý: Khi (Delta ABC = Delta DEF), ta cũng có thể viết (Delta BAC = Delta EDF) hay (Delta CBA = Delta FED);….

Giải bài 4.5 trang 67 SGK Toán 7 KNTT tập 1

Trong Hình 4.19, hãy chỉ ra hai cặp tam giác bằng nhau.

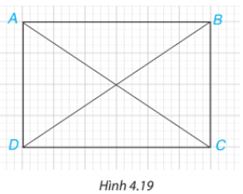
Phương pháp giải

Chỉ ra hai cặp tam giác có độ dài ba cặp cạnh bằng nhau.

Lời giải chi tiết

+) Xét (Delta ABC) và (Delta CDA) có:

AB=CD

DB chung

BC=AD

(Rightarrow Delta ABC)=(Delta CDA)(c.c.c)

+) Xét (Delta ABD) và (Delta CDB) có:

AB=CD

DB chung

AD=CB

(Rightarrow Delta ABD)=(Delta CDB)(c.c.c)

Giải bài 4.6 trang 67 SGK Toán 7 KNTT tập 1

Cho Hình 4.20, biết (AB = CB, AD = CD,widehat{DAB} = {90^circ },widehat{BDC} = {30^circ })

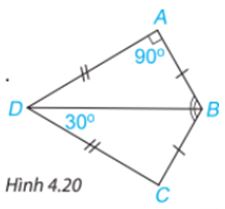
a) Chứng minh rằng (Delta ABD = Delta CBD).

b) Tính (widehat {ABC}).

Phương pháp giải

a) Chứng minh ba cặp cạnh của hai tam giác bằng nhau.

b) (widehat {ABC} = widehat {ABD} + widehat {CBD})

Lời giải chi tiết

a) Xét (Delta ABD) và (Delta CBD)có:

DA=DC(gt)

BD chung

BA=BC

Vậy (Delta ABD = Delta CBD)(c.c.c)

b) Ta có (widehat A = widehat C = {90^o})(hai góc tương ứng)

(begin{array}{l}widehat C + widehat {CDB} + widehat {DBC} = {180^o}\ Rightarrow {90^o} + {30^o} + widehat {DBC} = {180^o}\ Rightarrow widehat {DBC} = {60^o}end{array})

Mà (Delta ABD = Delta CBD) nên (widehat {ABD} = widehat {CBD}) ( 2 góc tương ứng)

(Rightarrow widehat {ABD} = widehat {CBD} = {60^o}\Rightarrow widehat {ABC} = widehat {ABD} + widehat {CBD} = {60^o} + {60^o} = {120^o})

==============