Giải bài 7 trang 56 SBT Toán 10 – CTST

Giải bài 7 trang 56 SBT Toán 10 – CTST – CHÂN TRỜI SÁNG TẠO
THUỘC BÀI SỐ: Bài 2. Hàm số bậc hai – SBT Toán 10 CTST

=======

Đề bài

Giả sử hàm số bậc hai mô phỏng vòm phía trong một trụ của cầu nhật tân là:

                             \(y = f\left( x \right) =  – \frac{{187}}{{856}}{x^2} + \frac{{8041}}{{856}}x\) (đơn vị đo: mét)

a) Hãy tính chiêu dài đoạn dây dọi sử dụng nếu khoảng cách từ chân của trụ cầu đễn quả nặng là 30 cm

b) Hãy tính khoảng cách từ chân trụ cầu đến quả nặng nếu biết chiều dài đoạn dây dọi sử dụng là 15 m

Phương pháp giải – Xem chi tiết

Bước 1: Xác định x, y từ yêu cầu bài toán

Bước 2: Thay tọa đồ vừa tìm được vào phương trình và tìm giá trị còn lại

Lời giải chi tiết

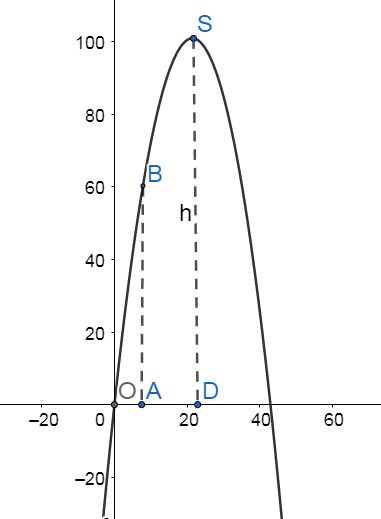
Mô phỏng các giả thiết bài toán bằng hình vẽ dưới đây

a) Khoảng cách từ chân trụ của cầu tới quả dọi là 30 cm tương ứng với  \(OA = 0,3 \Rightarrow {x_B} = 0,3\), chiều dài dây dọi tương ứng với  \({y_B}\)

Thay \(x = 0,3\) vào phương trình \(y = f\left( x \right) =  – \frac{{187}}{{856}}{x^2} + \frac{{8041}}{{856}}x\) ta tìm được:

\(y = f\left( {0,3} \right) =  – \frac{{187}}{{856}}{\left( {0,3} \right)^2} + \frac{{8041}}{{856}}\left( {0,3} \right) \simeq 2,8\)

Vậy khi khoảng cách từ chân trụ của cầu tới quả dọi là 30 cm thì chiều dại dây dọi gần bằng 2,8 m

b) Chiều dài dây dọi tương ứng với  \({y_B} = 15\) và khoảng cách từ chân trụ của cầu tới quả dọi tương ứng với  \({x_B}\)

Thay \({y_B} = 15\) vào phương trình \(y = f\left( x \right) =  – \frac{{187}}{{856}}{x^2} + \frac{{8041}}{{856}}x\) ta có:

\(15 =  – \frac{{187}}{{856}}{\left( {{x_B}} \right)^2} + \frac{{8041}}{{856}}\left( {{x_B}} \right) \Rightarrow \left[ \begin{array}{l}{x_B} \simeq 1,6\\{x_B} \simeq 41,3\end{array} \right.\)

Vậy khoảng cách từ chân trụ cầu đến quả nặng khi chiều dài dây dọi có thể là 1,6m và 41,3 m tính từ chân cầu bên trái

============

Thuộc chủ đề: Giải sách bài tập toán 10 – CHÂN TRỜI