Giải bài 6 trang 55 SBT Toán 10 – CTST

Giải bài 6 trang 55 SBT Toán 10 – CTST – CHÂN TRỜI SÁNG TẠO
THUỘC BÀI SỐ: Bài 2. Hàm số bậc hai – SBT Toán 10 CTST

=======

Đề bài

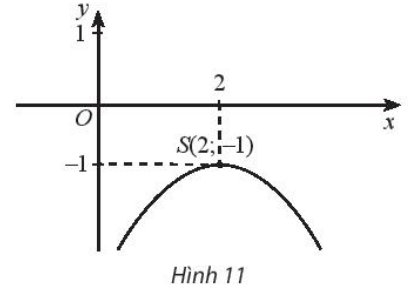
Tìm tập xác định, giá trị lớn nhất của hàm số, tập giá trị và các khoảng biến thiên của hàm số biết đồ thị hàm số là một parabol có đỉnh S như hình 11

Lời giải chi tiết

Hàm số có đồ thị là một parabol nê đó là hàm số bậc hai, suy có có tập xác định \(D = \mathbb{R}\)

Từ đồ thị hàm số ta thấy rằng, parabol quay bề lõm xuống dưới và có đỉnh \(S\left( {2; – 1} \right)\) nên có bảng biến thiên như sau:

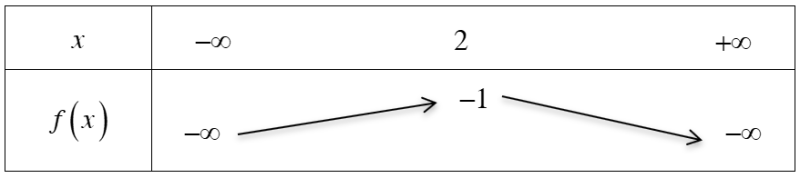
Từ bảng biến thiên ta có: giá trị lớn nhất của hàm số là \( – 1\), tập giá trị của hàm số là \(T = \left( { – \infty ; – 1} \right]\), đồng biến trên khoảng \(\left( { – \infty ; – 1} \right)\) và nghịch biến trên khoảng \(\left( { – 1; + \infty } \right)\)

============

Thuộc chủ đề: Giải sách bài tập toán 10 – CHÂN TRỜI