
Câu hỏi:
Cho đồ thị hàm số \(y = a{x^4} + b{x^2} + c\) đạt cực đại tại A(0;3) và cực tiểu B(-1;-5). Tính giá trị của 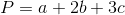 .
.
- A. P=-5
- B. P=-9
- C. P=-15
- D. P=3
Hãy chọn trả lời đúng trước khi xem đáp án và lời giải bên dưới.
Có vấn đề về lời giải xin các bạn để lại phản hồi cuối bài.
Đáp án đúng: C
\(y’ = 4a{x^3} + 2bx\)
Hàm số đạt cực đại tại A(0;-3) ta có: y’(0)=0; y (0)=-3 suy ra c=-3.
Hàm số đạt cực tiểu tại B(-1;-5) ta có: y’(-1) = 0; y (-1)=-5
Suy ra: \(\left\{ \begin{array}{l} – 4a – 2b = 0\\ a + b – 3 = – 5 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} a = 2\\ b = – 4 \end{array} \right.\)
Thay vào P ta có: P=2-8-9 =-15.
======
Các bạn xem lại Lý thuyết cực trị hàm số.
