Bài 4: Hệ trục tọa độ – Hướng dẫn giải bài 1.36, 1.37, 1.38, 1.39 trang 43; bài 1.40, 1.41, 1.42, 1.43, 1.44, 1.45, 1.46, 1.47 trang 44 Sách bài tập (SBT) Toán Hình lớp 10 .
Bài 1.36 trang 43
Viết tọa độ của các vec tơ sau:
\(\overrightarrow a = 2\overrightarrow i + 3\overrightarrow j\)
\(\overrightarrow b = {1 \over 3}\overrightarrow i – 5\overrightarrow j \)
\(\overrightarrow c = 3\overrightarrow i \)
\(\overrightarrow d = – 2\overrightarrow j \)
Gợi ý làm bài
\(\eqalign{
& \overrightarrow a = (2;3); \cr
& \overrightarrow b = 2({1 \over 3}; – 5); \cr
& \overrightarrow c = (3;0); \cr
& \overrightarrow d = (0; – 2). \cr} \)
Bài 1.37 trang 43 SBT Toán 10
Viết vec tơ \(\overrightarrow u \) dưới dạng \(\overrightarrow u = x\overrightarrow i + y\overrightarrow j \) khi viết tọa độ của \(\overrightarrow u \) là:
\((2; – 3),( – 1;4),(2;0),(0; – 1),(0;0)\)
Giải
\(\overrightarrow u = (2; – 3) = > \overrightarrow u = 2\overrightarrow i – 3\overrightarrow j \)
\(\overrightarrow u = ( – 1;4) = > \overrightarrow u = – \overrightarrow i + 4\overrightarrow j \)
\(\overrightarrow u = (2;0) = > \overrightarrow u = 2\overrightarrow i \)
\(\overrightarrow u = (0; – 1) = > \overrightarrow u = – \overrightarrow j \)
\(\overrightarrow u = (0;0) = > \overrightarrow u = 0\overrightarrow i + 0\overrightarrow j = \overrightarrow 0 \)
Bài 1.38 trang 43
Cho \(\overrightarrow a = (1; – 2),\overrightarrow b (0;3)\). Tìm tọa độ của các vec tơ \(\overrightarrow x = \overrightarrow a + \overrightarrow b ,\overrightarrow y = \overrightarrow a – \overrightarrow b ,\overrightarrow z = 3\overrightarrow a – 4\overrightarrow b \)
Bài giải
\(\vec x = \vec a + \vec b \Rightarrow \left\{ \matrix{
x_{\vec x}^{} = x_{\vec a}^{} + x_{\vec b}^{} = 1 \hfill \cr
y_{\vec x}^{} = y_{\vec a}^{} + y_{\vec b}^{} = 1 \hfill \cr} \right.\)
\(\vec y = \vec a – \vec b \Rightarrow \left\{ \matrix{
x_{\vec y}^{} = x_{\vec a}^{} – x_{\vec b}^{} = 1 \hfill \cr
y_{\vec y}^{} = y_{\vec a}^{} – y_{\vec b}^{} = – 5 \hfill \cr} \right.\)
\(\vec z = 3\vec a – 4\vec b \Rightarrow \left\{ \matrix{
x_{\vec z}^{} = 3x_{\vec a}^{} – 4x_{\vec b}^{} = 3 \hfill \cr
y_{\vec z}^{} = 3y_{\vec a}^{} – 4y_{\vec b}^{} = – 18 \hfill \cr} \right.\)
Bài 1.39
Xét xem các cặp vec tơ sau có cùng phương không? Trong trường hợp cùng phương thì xét xem chúng cùng hướng hay ngược hướng.
a) \(\overrightarrow a = (2;3),\overrightarrow b = ( – 10; – 15)\)
b) \(\overrightarrow u = (0;7),\overrightarrow v = (0;8)\)
c) \(\overrightarrow m = ( – 2;1),\overrightarrow b = ( – 6;3)\)
d) \(\overrightarrow c = (3;4),\overrightarrow d = (6;9)\)
e) \(\overrightarrow e = (0;5),\overrightarrow f = (3;0)\)
Gợi ý làm bài
a) \(\overrightarrow a ,\overrightarrow b \) ngược hướng;
b) \(\overrightarrow u ,\overrightarrow v \) cùng hướng;
c) \(\overrightarrow m ,\overrightarrow n \) cùng hướng;
d) \(\overrightarrow c ,\overrightarrow d \) không cùng phương;
e) \(\overrightarrow e ,\overrightarrow f \) hông cùng phương;
Bài 1.40 trang 44 SBT Toán 10
a) Cho \(A( – 1;8),B(1;6),C(3;4)\). Chứng minh ba điểm A, B, C thẳng hàng.
b) Cho \(A(1;1),B(3;2),C(m + 4;2m + 1)\). Tìm m để ba điểm A, B, C thẳng hàng.
Gợi ý
a) \(\overrightarrow {AB} = (2; – 2),\overrightarrow {AC} = (4; – 4)\)
Vậy \(\overrightarrow {AC} = 2\overrightarrow {AB} \) =>ba điểm A, B, C thẳng hàng.
b) \(\overrightarrow {AB} = (2;1),\overrightarrow {AC} = (m + 3;2m)\)
Ba điểm A, B, C thẳng hàng \( \Leftrightarrow {{3m} \over 2} = {{2m} \over 2} \Leftrightarrow m = 1\)
Bài 1.41 trang 44
Cho bốn điểm \(A( – 2; – 3),B(3;7),C(0;3),D( – 4; – 5)\).
Chứng minh rằng hai đường thẳng AB và CD song song với nhau.
Hướng dẫn giải
\(\overrightarrow {AB} = (5;10),\overrightarrow {CD} = ( – 4; – 8)\). Ta có: \(\overrightarrow {CD} = – {4 \over 5}\overrightarrow {AB} \), vậy hai đường thẳng AB và CD song song hoặc trùng nhau.
Ta có \(\overrightarrow {AC} = (2;6)\) và \(\overrightarrow {AB} \) không trùng phương vì \({5 \over 2} \ne {{10} \over 6}\)
Vậy AB // CD
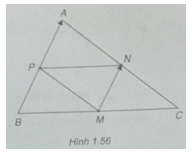
Bài 1.42 trang 44
Cho tam giác ABC. Các điểm \(M(1;1),N(2;3),P(0; – 4)\) lần lượt là trung điểm các cạnh BC, CA, AB. Tính tọa độ các đỉnh của tam giác.

\(\overrightarrow {MN} = (1;2)\)
\(\overrightarrow {PA} = ({x_A};{y_A} + 4)\)
Vì \(\overrightarrow {PA} = \overrightarrow {MN} \) suy ra
\(\left\{ \matrix{
{x_A} = 1 \hfill \cr
{y_A} + 4 = 2 \hfill \cr} \right. = > \left\{ \matrix{
{x_A} = 1 \hfill \cr
{y_A} = – 2 \hfill \cr} \right.\)
Tương tự, ta tính được
\(\left\{ \matrix{
{x_B} = – 1 \hfill \cr
{y_B} = – 6 \hfill \cr} \right. = > \left\{ \matrix{
{x_C} = 3 \hfill \cr
{y_C} = 8 \hfill \cr} \right.\)
Vậy tọa độ các đỉnh của tam giác là \(A(11; – 2),B( – 1; – 6),C(3;8)\)
Bài 1.43 trang 44
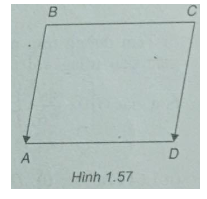
Cho hình bình hành ABCD. Biết \(A(2; – 3),B(4;5),C(0; – 1)\). Tính tọa độ của đỉnh D.
\(\overrightarrow {BA} = ( – 2; – 8)\)
\(\overrightarrow {CD} = ({x_D};{y_D} + 1)\). Vì \(\overrightarrow {BA} = \overrightarrow {CD} \) nên
\(\left\{ \matrix{
{x_D} = – 2 \hfill \cr
{y_D} + 1 = – 8 \hfill \cr} \right. = > \left\{ \matrix{
{x_D} = – 2 \hfill \cr
{y_D} = – 9 \hfill \cr} \right.\)
Vậy tọa độ đỉnh D(-2; -9)
Nhận xét: Ta có thể tính tọa độ đỉnh D dựa vào biểu thức \(\overrightarrow {BD} = \overrightarrow {BA} + \overrightarrow {BC} \)
Bài 1.44 trang 44
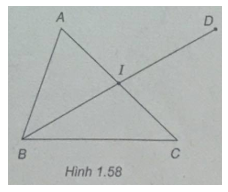
Cho tam giác ABC có A( – 5;6), B( – 4; – 1), C(4;3). Tìm tọa độ trung điểm I của AC. Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành.
Gọi I là trung điểm của AC
\(\eqalign{
& {x_I} = {{ – 5 + 4} \over 2} = – {1 \over 2}, \cr
& {y_I} = {{6 + 3} \over 2} = {9 \over 2} \cr} \)
Tứ giác ABCD là hình bình hành I là trung điểm của BD.
Vậy
\(\eqalign{
& \left\{ \matrix{
{{{x_D} – 4} \over 2} = – {1 \over 2} \hfill \cr
{{{y_D} – 1} \over 2} = {9 \over 2} \hfill \cr} \right. = > \left\{ \matrix{
{x_D} – 4 = – 1 \hfill \cr
{y_D} – 1 = 9 \hfill \cr} \right. \cr
& = > \left\{ \matrix{
{x_D} = 3 \hfill \cr
{y_D} = 10 \hfill \cr} \right. \cr} \)
Vậy tọa độ đỉnh D là (3;10).
Bài 1.45 trang 44 Toán 10
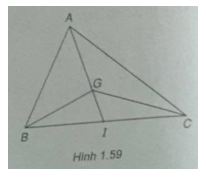
Cho tam giác ABC có A( – 3;6), B(9; – 10), C( – 5;4).
a) Tìm tọa độ của trọng tâm G của tam giác ABC
b) Tìm tọa độ điểm D sao cho tứ giác BGCD là hình bình hành
a) \(\left\{ \matrix{
{x_G} = {{ – 3 + 9 – 5} \over 3} = {1 \over 3} \hfill \cr
{y_G} = {{6 – 10 + 4} \over 3} = 0 \hfill \cr} \right.\)
b)Tứ giác BGCD là hình bình hành thì tọa độ điểm D là \(D({{11} \over 3}; – 6)\)
Bài 1.46
Cho tam giác đều ABC cạnh a. Chọn hệ tọa độ \((O;\overrightarrow i ,\overrightarrow j )\), trong đó O là trung điểm của cạnh BC, cùng hướng với , cùng hướng với .
a) Tính tọa độ của các đỉnh của tam giác ABC.
b) Tìm tọa độ trung điểm E của AC.
c) Tìm tọa độ tâm đường tròn ngoại tiếp tam giác ABC.
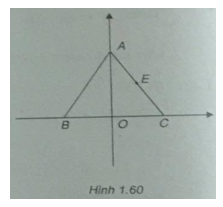
a) Ta có: Tam giác ABC cạnh a mà B là trung điểm BC nên \(OC = OB = {a \over 2}\)
\( \Rightarrow C\left( {{a \over 2};0} \right)$ và $B\left( { – {a \over 2};0} \right)\)
\(\eqalign{
& AO = \sqrt {{\rm{AC}}_{}^2 – {\rm{OC}}_{}^2} = \sqrt {a_{}^2 – \left( {{a \over 2}} \right)_{}^2} \cr
& = {{a\sqrt 3 } \over 2} \Rightarrow {\rm{A}}\left( {0;{{a\sqrt 3 } \over 2}} \right) \cr} \)
b) E là trung điểm AC
\( \Rightarrow \left\{ \matrix{
x_{\rm{E}}^{} = {{x_{\rm{A}}^{} + x_{\rm{C}}^{}} \over 2} = {a \over 4} \hfill \cr
y_{\rm{E}}^{} = {{y_{\rm{A}}^{} + y_{\rm{C}}^{}} \over 2} = {{a\sqrt 3 } \over 4} \hfill \cr} \right.\)
c) Do tam giác ABC đều nên tâm đường tròn ngoại tiếp tam giác trùng với trọng tâm G.
\(\left\{ \matrix{
x_{\rm{G}}^{} = {{x_{\rm{A}}^{} + x_{\rm{B}}^{} + x_{\rm{C}}^{}} \over 3} = 0 \hfill \cr
y_{\rm{G}}^{} = {{y_{\rm{A}}^{} + y_{\rm{B}}^{} + y_{\rm{C}}^{}} \over 3} = {{a\sqrt 3 } \over 6} \hfill \cr} \right.\)
Bài 1.47 trang 44
Cho lục giác ABCDEF. Chọn hệ tọa độ \((O;\overrightarrow i ,\overrightarrow j )\), trong đó O là tâm của lục giác đều, hai véc tơ \(\overrightarrow i \) và \(\overrightarrow {OD} \) cùng hướng, \(\overrightarrow j \) và \(\overrightarrow {EC} \) cùng hướng . Tính tọa độ các đỉnh của lục giác biết độ dài của lục giác là 6.
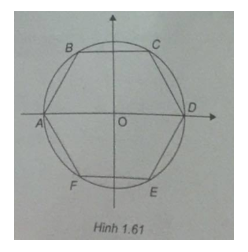
Do ABCDEF là lục giác đều nên \(AD = 2BC = 12 \Rightarrow AO = OD = 6\)
\( \Rightarrow A( – 6;0),D(6;0)\)
Gọi C’ là hình chiếu của C trên Ox
\(\eqalign{
& \Rightarrow OC’ = DC’ = 3 \cr
& \Rightarrow CC’ = \sqrt {CD_{}^2 – DC'{}^2} = \sqrt {6_{}^2 – 3_{}^2} = 3\sqrt 3 \cr} \)
\( \Rightarrow C(3;3\sqrt 3 )\)
B đối xứng với C qua Oy nên \(B( – 3;3\sqrt 3 )\)
E đối xứng với C qua Ox nên \(E(3; – 3\sqrt 3 )\)
F đối xứng với C qua O nên \(F( – 3; – 3\sqrt 3 )\)
