GIẢI CHI TIẾT Giải SBT Bài 3 Chương 7 – SBT Toán 10 CÁNH DIỀU
===========
Giải bài 24 trang 73 SBT Toán 10 Cánh diều tập 2 – CD
Cho đường thẳng ∆: 2x − 3y + 5 = 0. Vectơ nào dưới đây là một vectơ pháp tuyến của ∆?
A. \(\overrightarrow {{n_1}} = (2; – 3)\)
B. \(\overrightarrow {{n_2}} = ( – 3;2)\)
C. \(\overrightarrow {{n_3}} = (2;3)\)
D. \(\overrightarrow {{n_4}} = (3;2)\)
Phương pháp giải
Đường thẳng ax + by + c = 0 có vectơ pháp tuyến \(\overrightarrow n = (a;b)\)
Lời giải chi tiết
∆: 2x − 3y + 5 = 0 có vectơ pháp tuyến là \(\overrightarrow n = (2; – 3)\)
Chọn A
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 3
Giải bài 25 trang 73 SBT Toán 10 Cánh diều tập 2 – CD
Cho đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 3 – t\\y = 4 + 2t\end{array} \right.\). Vectơ nào dưới đây là một vectơ chỉ phương của ∆?
A. \(\overrightarrow {{u_1}} = (3;4)\)
B. \(\overrightarrow {{u_2}} = ( – 2;1)\)
C. \(\overrightarrow {{u_3}} = ( – 1;2)\)
D. \(\overrightarrow {{u_4}} = ( – 2; – 1)\)
Phương pháp giải
Đường thẳng \(\Delta :\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\end{array} \right.\) có vectơ chỉ phương \(\overrightarrow u = (a;b)\)
Lời giải chi tiết
\(\Delta :\left\{ \begin{array}{l}x = 3 – t\\y = 4 + 2t\end{array} \right.\) có một vectơ chỉ phương là \(\overrightarrow u = ( – 1;2)\)
Chọn C
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 3
Giải bài 26 trang 73 SBT Toán 10 Cánh diều tập 2 – CD
Cho đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 2 – 5t\\y = – 1 + 3t\end{array} \right.\). Trong các điểm có tọa độ dưới đây điểm nào nằm trên đường thẳng ∆?
A. (-3; -2)
B. (2; -1)
C. (-2; 1)
D. (-5; 3)
Phương pháp giải
Bước 1: Tìm điểm đi qua trên phương trình đường thẳng
Bước 2: Nếu không có điểm trên PT, thay tọa độ các điểm và giải tìm t, nếu 2 giá trị t trong hệ giống nhau thì điểm đó thuộc ∆
Lời giải chi tiết
Ta thấy điểm (2; -1) thuộc đường thẳng ∆
Chọn B
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 3
Giải bài 27 trang 73 SBT Toán 10 Cánh diều tập 2 – CD
Cho đường thẳng ∆: x − 3y + 4 = 0. Phương trình nào dưới đây là phương trình tham số của ∆?
A. \(\left\{ \begin{array}{l}x = – 1 + 3t\\y = – 1 + t\end{array} \right.\)
B. \(\left\{ \begin{array}{l}x = – 1 + 3t\\y = 1 + t\end{array} \right.\)
C. \(\left\{ \begin{array}{l}x = – 1 – 3t\\y = 1 + t\end{array} \right.\)
D. \(\left\{ \begin{array}{l}x = 1 – 3t\\y = 1 – t\end{array} \right.\)
Phương pháp giải
Bước 1: Tìm 1 vectơ chỉ phương của ∆ (lấy 1 vectơ nhân vô hướng với VTPT của ∆ bằng 0)
Bước 2: Tìm 1 điểm đi qua của ∆ (có thể thử các điểm trong đáp án)
Lời giải chi tiết
∆ có VTPT là \(\overrightarrow n = (1; – 3) \Rightarrow \)VTCP của ∆ là \(\overrightarrow {{u_1}} = (3;1)\)hoặc \(\overrightarrow {{u_2}} = ( – 3; – 1)\) Loại C
Xét điểm (-1; 1) ta có -1 – 3.1 + 4 = 0 \( \Rightarrow ( – 1;1) \in \Delta \)
Chọn B
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 3
Giải bài 28 trang 73 SBT Toán 10 Cánh diều tập 2 – CD
Cho đường thẳng \(\Delta :\left\{ \begin{array}{l}x = – 2 + 2t\\y = 3 – 5t\end{array} \right.\). Phương trình nào dưới đây là phương trình tổng quát của ∆?
A. 5x + 2y – 4 = 0
B. 2x – 5y + 19 = 0
C. -5x + 2y – 16 = 0
D. 5x + 2y + 4 = 0
Phương pháp giải
Bước 1: Tìm 1 vectơ pháp tuyến của ∆ (lấy 1 vectơ nhân vô hướng với VTCP của ∆ bằng 0)
Bước 2: Tìm 1 điểm đi qua của ∆ (Lấy điểm trong PT tham số)
Bước 3: Tìm PT tổng quát thỏa mãn 2 điều kiện trên
Lời giải chi tiết
∆ có VTCP là \(\overrightarrow u = (2; – 5) \Rightarrow \)VTPT của ∆ là \(\overrightarrow {{u_1}} = (5;2)\)hoặc \(\overrightarrow {{u_2}} = ( – 5; – 2)\) Loại B, C
∆ có điểm đi qua là (-2; 3)
PTTQ của ∆ là: 5x + 2y + 4 = 0
Chọn D
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 3
Giải bài 29 trang 73 SBT Toán 10 Cánh diều tập 2 – CD
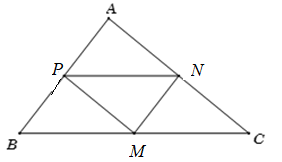
Cho tam giác ABC, biết toạ độ trung điểm các cạnh BC, CA, AB lần lượt là M(-1 ; 1), N(3 ; 4), P(5 ; 6).
a) Viết phương trình tham số của các đường thẳng AB, BC, CA
b) Viết phương trình tổng quát của các đường trung trực của tam giác ABC
Phương pháp giải
Bước 1: Tìm tọa độ các vectơ \(\overrightarrow {MN} ,\overrightarrow {MP} ,\overrightarrow {NP} \) rồi xác định các VTCP của AB, BC, CA
Bước 2: Viết PT tham số của các đường thẳng AB, BC, CA khi biết điểm đi qua và VTCP
Bước 3: Tìm các VTPT của các đường trung trực của ∆ABC là các vectơ \(\overrightarrow {MN} ,\overrightarrow {MP} ,\overrightarrow {NP} \)
Bước 4: Viết PTTQ các đường trung trực của tam giác ABC
Lời giải chi tiết

a) Theo giả thiết, MN, MP, NP là các đường trung bình của ∆ABC \( \Rightarrow MN//AB,MP//AC,NP//BC\)
Khi đó, AB, AC, BC lần lượt nhận các vectơ \(\overrightarrow {MN} = (4;3),\overrightarrow {MP} = (6;5),\overrightarrow {NP} = (2;2)\) làm VTCP
+ AB đi qua P, nhận \(\overrightarrow {MN} = (4;3)\) làm VTCP nên có PT tham số: \(\left\{ \begin{array}{l}x = 5 + 4t\\y = 6 + 3t\end{array} \right.\)
+ AC đi qua N, nhận \(\overrightarrow {MP} = (6;5)\) làm VTCP nên có PT tham số: \(\left\{ \begin{array}{l}x = 3 + 6k\\y = 4 + 5k\end{array} \right.\)
+ BC đi qua M, nhận \(\overrightarrow u = (1;1)\)cùng phương với \(\overrightarrow {NP} = (2;2)\) làm VTCP nên có PT tham số:
\(\left\{ \begin{array}{l}x = – 1 + p\\y = 1 + p\end{array} \right.\)
b) Ta có:
+ Đường trung trực của cạnh AB đi qua P và nhận \(\overrightarrow {MN} = (4;3)\) làm VTPT nên có PTTQ:
4x + 3y – 38 = 0
+ Đường trung trực của cạnh AC đi qua N và nhận \(\overrightarrow {MP} = (6;5)\) làm VTPT nên có PTTQ:
6x + 5y – 38 = 0
+ Đường trung trực của cạnh BC đi qua M và nhận \(\overrightarrow {NP} = (2;2)\) làm VTPT nên có PTTQ:
2x + 2y = 0 \( \Leftrightarrow x + y = 0\)
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 3
Giải bài 30 trang 73 SBT Toán 10 Cánh diều tập 2 – CD
Cho tam giác ABC có A(3 ; 7), B(–2 ; 2), C(6 ; 1). Viết phương trình tổng quát của các đường cao của tam giác ABC.
Phương pháp giải
Bước 1: Tìm tọa độ VTPT của các đường cao là cạnh đối diện tương ứng
Bước 2: Tìm điểm đi qua là các đỉnh của tam giác
Bước 3: Viết PTTQ của các đường cao khi biết điểm đi qua và VTPT tương ứng
Lời giải chi tiết
Ta có: \(\overrightarrow {AB} = ( – 5; – 5),\overrightarrow {AC} = (3; – 6),\overrightarrow {BC} = (8; – 1)\)
Gọi AH, BM, CN là các đường cao của ∆ABC. Khi đó:
+ \(AH \bot BC \Rightarrow \) AH đi qua A và nhận \(\overrightarrow {BC} = (8; – 1)\) làm VTPT nên có PT: 8x – y – 17 = 0
+ \(BM \bot AC \Rightarrow \) BM đi qua B và nhận \(\overrightarrow {{n_1}} = (1; – 2)\) cùng phương với \(\overrightarrow {AC} = (3; – 6)\) làm VTPT nên có PT:
x – 2y + 6 = 0
+ \(CN \bot AB \Rightarrow \) CN đi qua C và nhận \(\overrightarrow {{n_2}} = (1;1)\) cùng phương với \(\overrightarrow {AB} = ( – 5; – 5)\) làm VTPT nên có PT:
x + y – 7 = 0
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 3
Giải bài 31 trang 74 SBT Toán 10 Cánh diều tập 2 – CD
Cho đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 4 + t\\y = – 1 + 2t\end{array} \right.\) và điểm A(2 ; 1). Hai điểm M, N nằm trên ∆.
a) Tìm toạ độ điểm M sao cho AM = \(\sqrt {17} \)
b) Tìm toạ độ điểm N sao cho đoạn thẳng AN ngắn nhất
Phương pháp giải
Bước 1: Tham số hóa điểm M và N theo PT tham số ∆
Bước 2: Sử dụng công thức khoảng cách để lập biểu thức độ dài AM và AN
Bước 3: Giải PT để tìm tọa độ điểm M và đánh giá biểu thức độ dài AN để tìm điểm N thỏa mãn giả thiết
Lời giải chi tiết
Do \(M,N \in \Delta \) nên \(M(4 + t; – 1 + 2t)\) và \(N(4 + k; – 1 + 2k)\)
a) Ta có: \(\overrightarrow {AM} = (t + 2;2t – 2)\)
Theo giả thiết, AM = \(\sqrt {17} \) \( \Rightarrow A{M^2} = 17 \Leftrightarrow {(t + 2)^2} + {(2t – 2)^2} = 17\)\( \Leftrightarrow 5{t^2} – 4t – 9 = 0\)\( \Leftrightarrow \left[ \begin{array}{l}t = – 1\\t = \frac{9}{5}\end{array} \right.\)
Với t = -1 thì \(M(3; – 3)\)
Với \(t = \frac{9}{5}\) thì \(M\left( {\frac{{29}}{5};\frac{{13}}{5}} \right)\)
Vậy có 2 điểm M thỏa mãn là \(M(3; – 3)\) và \(M\left( {\frac{{29}}{5};\frac{{13}}{5}} \right)\)
b) Ta có: \(\overrightarrow {AN} = (k + 2;2k – 2)\)
\(AN = \sqrt {{{\left( {k + 2} \right)}^2} + {{(2k – 2)}^2}} \)\( \Leftrightarrow A{N^2} = {\left( {k + 2} \right)^2} + {(2k – 2)^2} \Leftrightarrow A{N^2} = 5{k^2} – 4k + 8\)
AN nhỏ nhất \( \Leftrightarrow A{N^2} = 5{k^2} – 4k + 8\) nhỏ nhất
Ta có: \(5{k^2} – 4k + 8 = 5{\left( {k – \frac{2}{5}} \right)^2} + \frac{{44}}{5}\)\( \Rightarrow A{N^2} \ge \frac{{44}}{5} \Rightarrow AN \ge \frac{{2\sqrt {55} }}{5}\)
Dấu “=” xảy ra khi và chỉ khi \(k = \frac{2}{5}\) \( \Rightarrow N\left( {\frac{{22}}{5}; – \frac{1}{5}} \right)\)
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 3
Giải bài 32 trang 74 SBT Toán 10 Cánh diều tập 2 – CD
Cho ba điểm A(-2 ; 2), B(7 ; 5), C(4 ; – 5) và đường thẳng ∆: 2x + y – 4 = 0
a) Tìm toạ độ điểm M thuộc ∆ và cách đều hai điểm A và B
b*) Tìm toạ độ điểm N thuộc ∆ sao cho |\(\overrightarrow {NA} + \overrightarrow {NB} + \overrightarrow {NC} \)| có giá trị nhỏ nhất.
Phương pháp giải
Bước 1: Tham số hóa điểm M và N theo PT tổng quát ∆
Bước 2: Sử dụng công thức khoảng cách để lập PT AM = BM
Bước 3: Giải PT để tìm tọa độ điểm M
Bước 4: Tìm tọa độ điểm I thỏa mãn \(\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} = \overrightarrow 0 \)
Bước 5: Biến đổi và tìm GTNN của biểu thức |\(\overrightarrow {NA} + \overrightarrow {NB} + \overrightarrow {NC} \)| để tìm điểm N thỏa mãn giả thiết
Lời giải chi tiết
a) Gọi \(M(t;4 – 2t) \in \Delta \)
Ta có: \(\overrightarrow {AM} = (t + 2; – 2t + 2)\), \(\overrightarrow {BM} = (t – 7; – 2t – 1)\)
Theo giả thiết, M cách đều hai điểm A và B \( \Rightarrow AM = BM \Leftrightarrow A{M^2} = B{M^2}\)
\( \Leftrightarrow {(t + 2)^2} + {( – 2t + 2)^2} = {(t – 7)^2} + {( – 2t – 1)^2}\)
\( \Leftrightarrow – 4t + 8 = – 10t + 50 \Leftrightarrow 6t = 42 \Leftrightarrow t = 7\)
Vậy M(7 ; -10)
b*) Ta có: \(\overrightarrow {AB} = (9;3),\overrightarrow {AC} = (6; – 7)\)
Vì \(\frac{9}{6} \ne \frac{3}{{ – 7}}\) nên \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) không cùng phương \( \Rightarrow A,B,C\) không thẳng hàng
Gọi G là trọng tâm ∆ABC \( \Rightarrow G\left( {3;\frac{2}{3}} \right)\) và \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \)
Xét \(\left| {\overrightarrow {NA} + \overrightarrow {NB} + \overrightarrow {NC} } \right| = \left| {\overrightarrow {NG} + \overrightarrow {GA} + \overrightarrow {NG} + \overrightarrow {GB} + \overrightarrow {NG} + \overrightarrow {GC} } \right|\)\( = \left| {3\overrightarrow {NG} } \right| = 3NG\)
\(\left| {\overrightarrow {NA} + \overrightarrow {NB} + \overrightarrow {NC} } \right|\) nhỏ nhất khi và chỉ khi NG nhỏ nhất \( \Leftrightarrow \) N là hình chiếu của G trên ∆
Gọi d là đường thẳng đi qua G, vuông góc với ∆
∆ có VTPT \(\overrightarrow n = (2;1)\) \( \Rightarrow \) ∆ có một VTCP là \(\overrightarrow u = (1; – 2)\)
Do \(d \bot \Delta \) nên d nhận \(\overrightarrow u = (1; – 2)\)làm VTPT \( \Rightarrow \) d có PT: 3x – 6y – 5 = 0
N là giao điểm của d và ∆ \( \Rightarrow \) tọa độ điểm N là nghiệm của hệ PT: \(\left\{ \begin{array}{l}2x + y – 4 = 0\\3x – 6y – 5 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{{29}}{{15}}\\y = \frac{2}{{15}}\end{array} \right.\)
Vậy \(N\left( {\frac{{29}}{{15}};\frac{2}{{15}}} \right)\)
GIẢI SBT Toán 10 Cánh Diều Chương 7 Bài 3
=======
THUỘC: Giải sách bài tập toán 10 – Cánh diều
