Giải bài tập Bài 4: Đường vuông góc và đường xiên (C8 Toán 7 Chân trời)

Giải bài tập Bài 4: Đường vuông góc và đường xiên (C8 Toán 7 Chân trời)
==========

Giải bài 1 trang 66 SGK Toán 7 Chân trời sáng tạo tập 2 – CTST

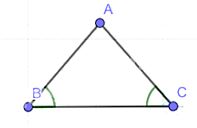
a) So sánh các góc của tam giác ABC có AB = 4 cm, BC = 7 cm, AC = 6 cm.

b) So sánh các cạnh của tam giác ABC có \(\widehat A\)\( = {50^o}\),\(\widehat C\)\( = {50^o}\)

Hướng dẫn giải chi tiết Bài 1

Phương pháp giải

– Sử dụng định lí về góc đối diện cạnh trong tam giác

– Sử dụng tính chất tam giác cân và tính góc còn lại của tam giác để so sánh độ dài các cạnh

Lời giải chi tiết

a) Theo đề bài ta có AB = 4cm, BC = 7cm, AC = 6cm

Có góc đối diện với cạnh AB là góc C, góc A đối diện với cạnh BC, góc B đối diện với cạnh AC

Theo định lí về góc đối diện với cạnh lớn hơn thì lớn hơn ta có :

\( \Rightarrow \widehat A > \widehat B > \widehat C\)

b)

Vì \(\widehat{B}=\widehat{C}\) nên tam giác ABC cân tại A

\( \Rightarrow AB = AC\)

Áp dụng định lí tổng 3 góc trong tam giác ABC, có:

\( \Rightarrow \widehat A = {180^o} – {100^0} = {80^o}\)

\( \Rightarrow \widehat A > \widehat B;\widehat C\)

\( \Rightarrow BC\) là cạnh lớn nhất tam giác ABC

Theo định lí về góc đối diện cạnh lớn hơn thì lớn hơn

 

–>

— *****

Giải bài 2 trang 66 SGK Toán 7 Chân trời sáng tạo tập 2 – CTST

Cho tam giác ABC có \(\widehat A = \)\({100^0}\),\(\widehat B\)\( = {40^o}\).

a) Tìm cạnh lớn nhất của tam giác ABC.

b) Tam giác ABC là tam giác gì? Vì sao?

Hướng dẫn giải chi tiết Bài 2

Phương pháp giải

– Sử dụng định lí về góc đối diện cạnh trong tam giác

– Sử dụng tính chất tam giác cân

Lời giải chi tiết

a) Theo định lí tổng 3 góc trong tam giác, ta có:

\( \Rightarrow \widehat A + \widehat B + \widehat C = {180^o}\)

\( \Rightarrow \widehat C = {180^o} – {100^o} – {40^o} = {40^o}\)

\( \Rightarrow \widehat A > \widehat C\) và \(\widehat A > \widehat B\)

\( \Rightarrow \) BC là cạnh lớn nhất của tam giác ABC do đối diện với góc A

b) Xét tam giác ABC có:

 \(\widehat C = \widehat B = {40^o}\)( chứng minh a )

\( \Rightarrow \) ABC là tam giác cân

 

–>

— *****

Giải bài 3 trang 66 SGK Toán 7 Chân trời sáng tạo tập 2 – CTST

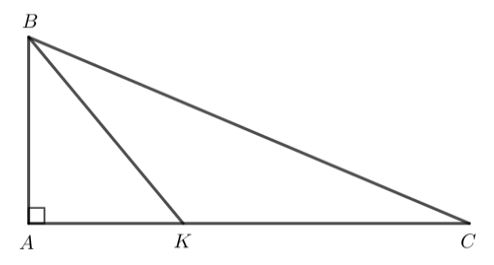
Cho tam giác ABC vuông tại A có \(\widehat B > {45^o}\)

a) So sánh các cạnh của tam giác

b) Lấy điểm K bất kì thuộc đoạn thẳng AC. So sánh độ dài BK và BC.

Hướng dẫn giải chi tiết Bài 3

Phương pháp giải

Sử dụng định lí về góc đối diện cạnh trong tam giác

Lời giải chi tiết

a) Vì tam giác ABC vuông tại A nên \(\widehat{A}=90^0; \widehat{B}+\widehat{C}=90^0\)

Vì \(\widehat B > {45^o} \Rightarrow \widehat C < {45^o} \Rightarrow \widehat A > \widehat B > \widehat C \Rightarrow BC > AC > AB\)

b) Vì \(\widehat {BKC}\) là góc ngoài tại đỉnh K của tam giác ABK nên \(\widehat {BKC}>\(\widehat {BAK}=90^0\)

Xét tam giác BCK, ta có :

\(\widehat {BKC} > {90^o} > \widehat {BCK}\)

\( \Rightarrow BC > BK\) ( quan hệ giữa góc và cạnh đối diện trong tam giác)

 

–>

— *****

Giải bài 4 trang 66 SGK Toán 7 Chân trời sáng tạo tập 2 – CTST

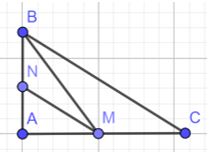
Quan sát Hình 10.

a) Tìm đoạn ngắn nhất trong các đoạn BA, BM, BC.

b) Tìm đoạn ngắn nhất trong các đoạn MA, MN, MB.

c) Chứng minh rằng MA < BC.

Hướng dẫn giải chi tiết Bài 4

Phương pháp giải

– Dựa vào tính chất từ 1 điểm ngoài đường thẳng thì đường vuông góc ngắn hơn các đường xiên .

– Ta chứng minh MA < AC < BC

Lời giải chi tiết

a) BA là đường vuông góc; 

BM và BC là các đường xiên kẻ từ B đến đường thẳng AC

Ta được đường ngắn nhất là đường thẳng vuông góc nên BA là đoạn ngắn nhất.

b) Tương tự câu a

MA là đường vuông góc; 

MN và MB là các đường xiên kẻ từ M đến đường thẳng AB

Ta được đường ngắn nhất là đường thẳng vuông góc nên MA là đoạn ngắn nhất.

c) Xét tam giác ABC vuông tại A

\( \Rightarrow \widehat A = {90^o}\)\( \Rightarrow \)A là góc lớn nhất tam giác ABC

\( \Rightarrow \) BC > AC ( định lí về góc đối diện và cạnh )

Vì M nằm giữa AC nên AM < AC

\( \Rightarrow \) AM < AC < BC

Vậy AM < BC

 

–>

— *****

Giải bài 5 trang 66 SGK Toán 7 Chân trời sáng tạo tập 2 – CTST

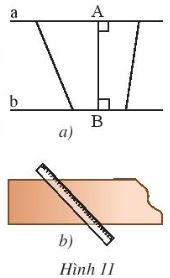
Trong Hình 11a, ta gọi độ dài đoạn thẳng AB là khoảng cách giữa hai đường thẳng song song a và b.

a) Một thanh nẹp gỗ có hai cạnh song song (Hình 11b). Chiều rộng của thanh nẹp gỗ là khoảng cách giữa hai cạnh đó. Hãy cho biết có phải chiều rộng của thanh nẹp gỗ là khoảng cách ngắn nhất từ một điểm trên cạnh này dến một điểm trên cạnh kia không.

b) Muốn đo chiều rộng của thanh nẹp, ta phải đặt thước như thế nào ? Vì sao?

Hướng dẫn giải chi tiết Bài 5

Phương pháp giải

Sử dụng mối quan hệ giữa đường vuông góc và đường xiên.

Lời giải chi tiết

a) Chiều rộng của thanh nẹp gỗ là khoảng cách ngắn nhất từ một điểm trên cạnh này đến một điểm trên cạnh kia (đoạn vuông góc là đoạn ngắn nhất )

b) Ta đặt thước vuông góc với 2 cạnh của nẹp vì chiều rộng của thanh nẹp là khoảng cách giữa 2 cạnh của nẹp

 

–>

— *****