Lý thuyết Bài 3: Giải tam giác và ứng dụng thực tế – Chân trời

Lý thuyết Bài 3: Giải tam giác và ứng dụng thực tế – Chân trời
============

1.1. Giải tam giác

Để giải tam giác, ta thường sử dụng một cách hợp lí cáe hệ thức hượng như: định lí sin, định lí côsin và các công thức tính điện tích tam giác.

Ví dụ: Giải tam giác ABC trong các trường hợp sau:

a) AB =85, AC =95 và \(\widehat A = {40^0}\),

b) AB = 15, AC=25 và BC=30.

Giải

Đặt a = BC, b =AC, c = AB

a) Ta cần tính cạnh a và hai góc \(\widehat B,\widehat C\) 

Áp dụng định lí côsin, ta có

aề=B3+ c°— 2becos.4=953 + 853— 2.95.85, cos40° 3878,38

Suy ra a= J3878,38 z 62,3

Áp dung hệ quả định lí côsin, ta có:

\({a^2} = {b^2} + {c^2} – 2.b.c.\cos A = {95^2} + {85^2} – 2.95.85.cos{40^0} \approx 3878,38\) 

Suy ra \(a \approx \sqrt {3878,38}  \approx 62,3\) 

Áp dụng hệ quả định lí côsin, ta có:

\(\cos B = \frac{{{a^2} + {c^2} – {b^2}}}{{2ac}} \approx \frac{{62,{3^2} + {{85}^2} – {{95}^2}}}{{2.62,3.85}} \approx 0,197\) 

Suy ra: \(\widehat B \approx {78^0}38′,\widehat C \approx {180^0} – {40^0} – {78^0}38′ = {61^0}22’\) 

1.2. Áp dụng giải tam giác vào thực tế

Vận dụng giải tam giác giúp ta giải quyết rât nhiêu bài toán trong thực tê, đặc biệt là trong thiết kế và xây dựng.

Ví dụ 1: Một đường hầm được dự kiến xây dựng xuyên qua một ngọn núi. Để ước tính chiều đài của đường hàm, một kĩ sư đã thực hiện các phép đo và cho ra kết quả như Hình sau. Tính chiều đài của đường hầm tử các số liệu đã khảo sát được.

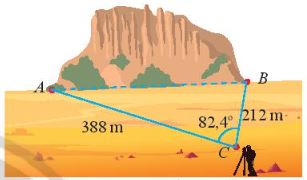
Giải

Áp dụng định lí côsin trong tam giác ABC, ta có:

\(A{B^2} = C{A^2} + C{B^2} – 2CA.CB.\cos C = 388{}^2 + {212^2} – 2.388.212.cos82,{4^0} \approx 173730\).

Suy ra: \(AB \approx \sqrt {173730}  = 417\left( m \right)\) 

Vậy đường hầm dài khoảng 417 m.

Ví dụ 2: 

Để xác định chiêu cao của một toà nhà cao tầng, một người đứng tại điểm AM, sử dụng giác kế nhìn thây đỉnh toà nhà với góc nâng \(\widehat {RQA} = {84^0}\), người đó lùi ra xa một khoảng cách LM = 49,4m thì nhìn thây đỉnh toà nhà với góc nâng \(\widehat {RPA} = {78^0}\). Tính chiều cao của toà nhà, biết rằng khoảng cách từ mặt đất đến ống ngắm của giác kê đó là PL = QM = 1,2m

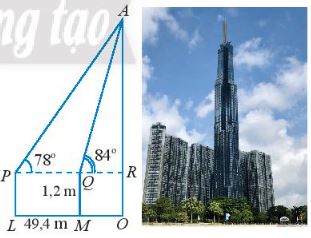
Giải

Ta có: \(\widehat {PAQ} = \widehat {AQR} – \widehat {APR} = {84^0} – {78^0} = {6^0}\).

Áp dụng định lí sin trong tam giác APQ, ta có:

\(\frac{{AQ}}{{\sin P}} = \frac{{PQ}}{{\sin A}} \Rightarrow \frac{{AQ}}{{\sin {{78}^0}}} = \frac{{PQ}}{{\sin {6^0}}} \Rightarrow AQ = \frac{{PQ.\sin {{78}^0}}}{{\sin {6^0}}}\) 

Trong tam giác vuông AQR, ta có:

\(AR = AQ.\sin {84^0} = \frac{{PQ.\sin {{78}^0}.\sin {{84}^0}}}{{\sin {6^0}}} = \frac{{49,4.\sin {{78}^0}.\sin {{84}^0}}}{{\sin {6^0}}} \approx 460\left( m \right)\) 

Vậy chiều cao của tòa nhà là \(AO = AR + RO \approx 460 + 1,2 = 461,2\left( m \right).\)

Câu 1:  Giải tam giác ABC trong các trường hợp sau:

a) \(a = 17,4;\widehat B = {44^o}30′;\widehat C = {64^o}.\)

b) \(a = 10;b = 6;c = 8.\)

Hướng dẫn giải

a) Ta cần tính góc \(\widehat A\) và hai cạnh \(b,c.\)

Ta có: \(\widehat A = {180^o} – \widehat B – \widehat C = {180^o} – {44^o}30′ – {64^o} = {71^o}30′.\)

Áp dụng định lí sin, ta có:

\(\begin{array}{l}\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} \Rightarrow \frac{{17,4}}{{\sin {{71}^o}30′}} = \frac{b}{{\sin {{44}^o}30′}} = \frac{c}{{\sin {{64}^o}}}\\ \Rightarrow \left\{ \begin{array}{l}b = \sin {44^o}30′.\frac{{17,4}}{{\sin {{71}^o}30′}} \approx 12,86\\c = \sin {64^o}.\frac{{17,4}}{{\sin {{71}^o}30′}} \approx 16,5\end{array} \right.\end{array}\)

b) Ta cần tính số đo ba góc \(\widehat A,\widehat B,\widehat C\)

Áp dụng hệ quả của định lí cosin, ta có:

 \(\begin{array}{l}\cos A = \frac{{{b^2} + {c^2} – {a^2}}}{{2bc}};\cos B = \frac{{{a^2} + {c^2} – {b^2}}}{{2ac}}\\ \Rightarrow \cos A = \frac{{{6^2} + {8^2} – {{10}^2}}}{{2.6.8}} = 0;\cos B = \frac{{{{10}^2} + {8^2} – {6^2}}}{{2.10.8}} = \frac{4}{5}\\ \Rightarrow \widehat A = {90^o},\widehat B = {36^o}52’11,63”\\ \Rightarrow \widehat C = {53^o}7’48,37”\end{array}\)

Câu 2:  Hai máy bay cùng cất cánh từ một sân bay nhưng bay theo hai hướng khác nhau. Một chiếc di chuyển với tốc độ 450 km/h theo hướng tây và chiếc còn lại di chuyển theo hướng lệch so với hướng bắc \({25^o}\) về phía tây với tốc độ 630 km/h (Hình sau). Sau 90 phút, hai máy bay cách nhau bao nhiêu kilomet? Giả sử chúng đang ở cùng độ cao.

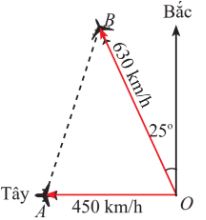
Hướng dẫn giải

Ta có: \(\widehat {BOA} = {90^o} – {25^o} = {75^o}.\)

Sau 90 phút = 1,5 giờ:

Máy bay thứ nhất đi được quãng đường (OA) là: \(450.1,5 = 675\;(km)\)

Máy bay thứ hai đi được quãng đường (OB) là: \(630.1,5 = 945\;(km)\)

Áp dụng định lí cosin trong tam giác OAB, ta có:

\(\begin{array}{l}A{B^2} = O{A^2} + O{B^2} – 2OA.OB\cos O\\ \Leftrightarrow A{B^2} = {675^2} + {945^2} – 2.675.945\cos {75^o}\\ \Rightarrow AB \approx 1009,2\end{array}\)

Vậy sau 90 phút, hai máy bay cách nhau khoảng 1009,2 km.

===========
Chuyên mục: Chương 4: Hệ thức lượng trong tam giác