Trả lời câu hỏi trong bài tập cuối chương IX trang 73 – Chân trời

Trả lời câu hỏi trong bài tập cuối chương IX trang 73 – Chân trời
============

Bài tập 1.  Trong mặt phẳng Oxy, cho bốn điểm A(2; 1), B(1; 4), C(4; 5), D(5; 2).

a. Chứng minh ABCD là hình vuông. 

b. Tìm tọa độ tâm I của hình vuông ABCD.

Hướng dẫn giải:

a. Ta có: $\vec{AB}$ = (-1; 3), $\vec{DC}$ = (-1; 3) $\Rightarrow$ $\vec{AB}$ = $\vec{DC}$ 

$\Rightarrow$ ABCD là hình bình hành.

Lại có: $\vec{AD}$ = (3; 1) $\Rightarrow$ $\vec{AB}$. $\vec{AD}$ = -1. 3 + 3. 1 = 0

$\Rightarrow$ $\vec{AB}$ $\perp$ $\vec{AD}$ hay AB $\perp$ AD

$\Rightarrow$ Hình bình hành ABCD là hình chữ nhật.

Ta có: AD = |$\vec{AD}$| = $\sqrt{3^{2} + 1^{2}}$ = $\sqrt{10}$

          AB = |$\vec{AB}$| = $\sqrt{(-1)^{2} + 3^{2}}$ = $\sqrt{10}$

$\Rightarrow$ AB = AD $\Rightarrow$ Hình chữ nhật ABCD là hình vuông (đpcm).

b. Tâm I của hình vuông ABCD là trung điểm của AC $\Rightarrow$ I = ($\frac{2 + 4}{2}$; $\frac{1+5}{2}$) $\Leftrightarrow$ I = (3; 3)

Vậy I = (3; 3).

Bài tập 2.  Cho AB và CD là dây cung vuông góc tại E của đường tròn (O). Vẽ hình chữ nhật AECF. Dùng phương pháp tọa độ để chứng minh EF vuông góc với DB.

Hướng dẫn giải:

Chọn hệ tọa độ Oxy như hình vẽ. A(a; 0), B(b; 0), C(0; c), D(0; d). Hai dây cung AB và CD vuông góc với nhau tại E (trùng với gốc tọa độ O).

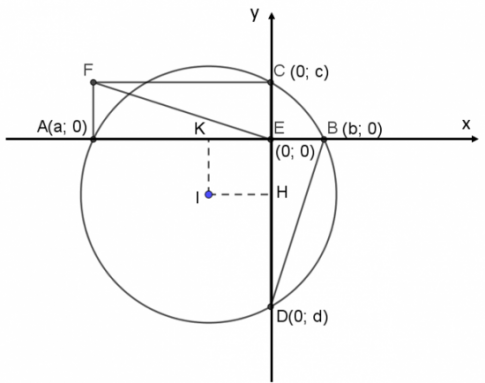
Vì ACEF là hình chữ nhật nên F(a; c). 

Gọi I là tâm đường tròn (O), K và H lần lượt là chân đường cao hạ từ I tới AB, CD.

$\Rightarrow$ K là trung điểm của AB $\Rightarrow$ K = ($\frac{a + b}{2}$; 0)

     H là trung điểm của CD $\Rightarrow$ H = (0; $\frac{c + d}{2}$)

$\Rightarrow$ I = ($\frac{a + b}{2}$; $\frac{c + d}{2}$)

Ta có: $\vec{IA}$ = (a – $\frac{a + b}{2}$; -$\frac{c + d}{2}$) = ($\frac{a – b}{2}$; -$\frac{c + d}{2}$)

         $\vec{IC}$ = ( -$\frac{a + b}{2}$; c – $\frac{c + d}{2}$) = (-$\frac{a + b}{2}$; $\frac{c – d}{2}$

Vì IA = IC (=R) $\Rightarrow$ $(\frac{a – b}{2})^{2}$ + $(-\frac{c + d}{2})^{2}$ = $(-\frac{a + b}{2})^{2}$ + $(\frac{c – d}{2})^{2}$

$\Leftrightarrow$ $(a – b)^{2}$ + $(c + d)^{2}$ = $(a + b)^{2}$ + $(c – d)^{2}$

$\Leftrightarrow$ $a^{2} – 2ab + b^{2} + c^{2} + 2cd + d^{2}$ = $a^{2} + 2ab + b^{2} + c^{2} – 2cd + d^{2}$

$\Leftrightarrow$ 4ab = 4cd $\Leftrightarrow$ ab = cd $\Leftrightarrow$ ab – cd = 0

Ta có: $\vec{EF}$ = (-a; -c}, $\vec{BD}$ = (-b; d)

$\Rightarrow$ $\vec{EF}$. $\vec{BD}$ = (-a).(-b) – c.d = ab – cd = 0 (chứng minh trên)

$\Rightarrow$ $\vec{EF}$ $\perp$ $\vec{BD}$ hay EF $\perp$ BD (đpcm).

===========
Chuyên mục: Học Toán lớp 10 – Chân trời