Trả lời câu hỏi trong bài 1 Giá trị lượng giác của một góc từ 0 độ đến 180 độ – Chân trời
============
1. GIÁ TRỊ LƯỢNG GIÁC
Khám phá 1: Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O bán kính R = 1 nằm phía trên trục hoành được gọi là nửa đường tròn đơn vị. Cho trước một góc nhọn $\alpha$, lấy điểm M trên nửa đường tròn đơn vị sao cho $\widehat{xOM}$ = $\alpha$. Giả sử điểm M có tọa độ ($x_{0}$; $y_{0}$). Trong tam giác vuông OHM, áp dụng cách tính các tỉ số lượng giác của một góc nhọn đã học ở lớp 9, chứng tỏ rằng:
sin$\alpha$ = $y_{0}$; cos$\alpha$ = $x_{0}$; tan$\alpha$ = $\frac{y_{0}}{x_{0}}$; cot$\alpha$ = $\frac{x_{0}}{y_{0}}$
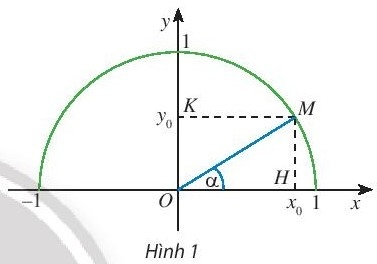
Hướng dẫn giải:
Xét tam giác OMH vuông tại H, ta có:
- sin$\alpha$ = $\frac{MH}{OM}$ = $\frac{y_{0}}{R}$ = $\frac{y_{0}}{1}$ = $y_{0}$
- cos$\alpha$ = $\frac{OH}{OM}$ = $\frac{x_{0}}{R}$ = $\frac{x_{0}}{1}$ = $x_{0}$
- tan$\alpha$ = $\frac{sin\alpha}{cos\alpha}$ = $\frac{y_{0}}{x_{0}}$
- cot$\alpha$ = $\frac{cos\alpha}{sin\alpha}$ = $\frac{x_{0}}{y_{0}}$
Thực hành 1: Tìm giá trị lượng giác góc $135^{\circ}$
Hướng dẫn giải:
Lấy điểm M trên nửa đường tròn đơn vị sao cho $\widehat{xOM}$ = $135^{\circ}$. Ta có: $\widehat{MOy}$ = $135^{\circ}$ – $90^{\circ}$ = $45^{\circ}$.
Lại có: sin$45^{\circ}$ = $\frac{\sqrt{2}}{2}$; cos$45^{\circ}$ = $\frac{\sqrt{2}}{2}$
$\Rightarrow$ Tọa độ điểm M là $\left ( – \frac{\sqrt{2}}{2}; \frac{\sqrt{2}}{2} \right)$.
Vậy theo định nghĩa ta có:
- sin$135^{\circ}$ = $\frac{\sqrt{2}}{2}$; cos$135^{\circ}$ = – $\frac{\sqrt{2}}{2}$
- tan$135^{\circ}$ = -1; cot$135^{\circ}$ = -1
2. QUAN HỆ GIỮA CÁC GIÁ TRỊ LƯỢNG GIÁC CỦA HAI GÓC BÙ NHAU
Khám phá 2: Trên nửa đường tròn đơn vị, cho dây cung NM song song với trục Ox (Hình 4). Tính tổng số đo của hai góc $\widehat{xOM}$ và $\widehat{xON}$.
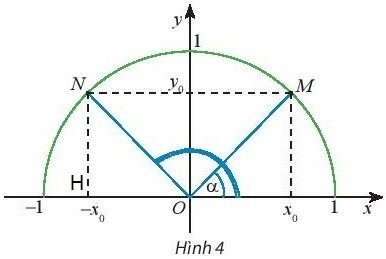
Hướng dẫn giải:
Gọi H là chân đường vuông góc hạ từ N xuống Ox.
Vì $\widehat{xOM}$ = $\widehat{HON}$ nên $\widehat{xOM}$ + $\widehat{xON}$ = $\widehat{HON}$ + $\widehat{xON}$ = $\widehat{HOx}$ = $180^{\circ}$
Thực hành 2: Tính các giá trị lượng giác: sin$120^{\circ}$; cos$150^{\circ}$, cot$135^{\circ}$
Hướng dẫn giải:
- sin$120^{\circ}$ = sin$(180^{\circ} – 60^{\circ})$ = $\frac{\sqrt{3}}{2}$
- cos$150^{\circ}$ = -cos$30^{\circ}$ = – $\frac{\sqrt{3}}{2}$
- cot$135^{\circ}$ = -cot$45^{\circ}$ = -1
Vận dụng 1: Cho biết sin$\alpha$ = $\frac{1}{2}$, tìm góc $\alpha$ ($0^{\circ} \leq \alpha \leq 180^{\circ}$) bằng cách vẽ nửa đường tròn đơn vị).
Hướng dẫn giải:
Theo định nghĩa, sin$\alpha$ = $y_{0}$ = $\frac{1}{2}$. Ta có hình vẽ:
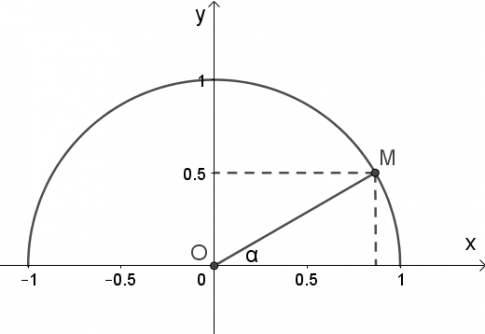
Đo $\alpha$ = $30^{\circ}$
3. GIÁ TRỊ LƯỢNG GIÁC CỦA CÁC GÓC ĐẶC BIỆT
Thực hành 3: Tính:
A = sin$150^{\circ}$ + tan$135^{\circ}$ + cot$45^{\circ}$;
B = 2cos$30^{\circ}$ – 3tan$150^{\circ}$ + cot$135^{\circ}$
Hướng dẫn giải:
A = sin$150^{\circ}$ + tan$135^{\circ}$ + cot$45^{\circ}$
= $\frac{1}{2}$ + (-1) + 1 = $\frac{1}{2}$
B = 2cos$30^{\circ}$ – 3tan$150^{\circ}$ + cot$135^{\circ}$
= 2.$\frac{\sqrt{3}}{2}$ – 3.(- $\frac{\sqrt{3}}{3}$ + (-1) = -1 + 2$sqrt{3}
Vận dụng 2: Tìm góc $\alpha$ ($0^{\circ} \leq \alpha \leq 180^{\circ}$) trong mỗi trường hợp sau:
a. sin$\alpha$ = $\frac{\sqrt{3}}{2}$;
b. cos$\alpha$ = $\frac{-\sqrt{2}}{2}$;
c. tan$\alpha$ = -1;
d. cot$\alpha$ = -$sqrt{3}$
Hướng dẫn giải:
a. $\alpha$ = $60^{\circ}$ hoặc $\alpha$ = $120^{\circ}$
b. $\alpha$ = $135^{\circ}$
c. $\alpha$ = $135^{\circ}$
d. $\alpha$ = $150^{\circ}$
4. SỬ DỤNG MÁY TÍNH CẦM TAY ĐỂ TÍNH GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC
Thực hành 4:
a. Tính cos$80^{\circ}$43’51”; tan$47^{\circ}$12’25”; cot$99^{\circ}$9’19”.
b. Tìm $\alpha$ ($0^{\circ} \leq \alpha \leq 180^{\circ}$), biết cos$\alpha$ = -0.723
Hướng dẫn giải:
a.
- cos$80^{\circ}$43’51” $\approx$ 0,161
- tan$47^{\circ}$12’25” $\approx$ 1,08
- cot$99^{\circ}$9’19” $\approx$ -0,161
b. $\alpha$ $\approx$ $136^{\circ}$18’10”
===========
Chuyên mục: Học Toán lớp 10 – Chân trời
