Lý thuyết Bài 7: Các khái niệm mở đầu
=============
Tóm tắt lý thuyết
1.1. Khái niệm vectơ
|
+ Vectơ là một đoạn thẳng có hướng, nghĩa là, trong hai điểm mút của đoạn thẳng, đã chỉ rõ điểm đâu, điểm cuối. + Độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó. |
|---|
Chú ý
+ Vectơ có điểm đầu A và điểm cuối B được kí hiệu là AB, đọc là vectơ AB
+ Để vẽ một vectơ, ta vẽ đoạn thẳng nói điềm đầu và điểm cuối của nó, rồi đánh dấu mũi tên ở điểm cuối

+ Vectơ còn được kí hiệu là \(\overrightarrow a ,\overrightarrow b ,\overrightarrow x ,\overrightarrow y ,…\)
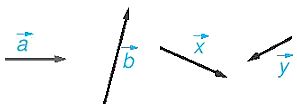
+ Độ dài của vectơ \(\overrightarrow {AB} \), \(\overrightarrow a\) tương ứng được kí hiệu là \(\left| {\overrightarrow {AB} } \right|,\left| {\overrightarrow a } \right|.\)
Ví dụ: Cho hình vuông ABCD với cạnh có độ dài bằng 1. Tính độ dài các vectơ \(\overrightarrow {AC} ,{\rm{ }}\overrightarrow {CA} ,{\rm{ }}\overrightarrow {BD} .\)
Giải
Vì cạnh của hình vuông ABCD có độ dài bằng 1 nên các đường chéo của hình vuông này có độ dài bằng \(\sqrt 2\).
Vậy \(\left| {\overrightarrow {AC} } \right| = AC = \sqrt 2 ,\left| {\overrightarrow {CA} } \right| = CA = \sqrt 2 ,\left| {\overrightarrow {B{\rm{D}}} } \right| = B{\rm{D}} = \sqrt 2 \)
1.2. Hai vectơ cùng phương, cùng hướng, bằng nhau
|
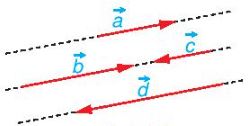
– Đường thẳng đi qua điểm đầu và điểm cuối của một vectơ được gọi là giá của vectơ đó. – Hai vectơ được gọi là cùng phương nếu chúng có giá song song hoặc trùng nhau. |
|---|
|
– Đối với hai vectơ cùng phương thì chúng cùng hướng hoặc ngược hướng. – Hai vectơ \(\overrightarrow a\) và \(\overrightarrow b\) được gọi là bằng nhau, kí hiệu \(\overrightarrow a = \overrightarrow b \), nếu chúng có cùng độ dài và cùng hướng. |
|---|

Chú ý
+ Ta cũng xét các vectơ có điểm đầu và điểm cuối trùng nhau (chăng hạn AA, 8B, MM). gọi là các vecto-không.
+ Ta quy ước vectơ-không có độ dài bằng 0, cùng hướng (do đó cùng phương) với mọi vectơ.
+ Các vecto-không có cùng độ dài và cùng hướng nên bằng nhau và được kí hiệu Chúng là \(\overrightarrow 0 \)
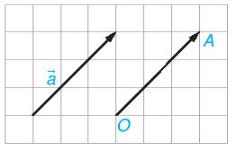
+ Với mỗi điểm O và vectơ \(\overrightarrow a \) cho trước, có duy nhất điểm A sao cho \(\overrightarrow {OA} = \overrightarrow a \)
Ví dụ: Cho hình chữ nhật ABCD. Hãy chỉ ra mối quan hệ về độ dài, phương, hướng giữa các cặp vecto: \(\overrightarrow {A{\rm{D}}} \) và \(\overrightarrow {BC} ,\overrightarrow {AB} \) và \(\overrightarrow {CD} ,\overrightarrow {AC} \) và \(\overrightarrow {BD} \). Những cặp vectơ nào trong các cặp vectơ trên là bằng nhau?
Giải
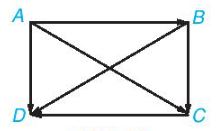
+ Hai vectơ \(\overrightarrow {A{\rm{D}}} \) và \(\overrightarrow {BC} \) có cùng độ dài và cùng hướng. Do đó, hai vectơ \(\overrightarrow {A{\rm{D}}} \) và \(\overrightarrow {BC} \) băng nhau.
+ Hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) có cùng độ dài và ngược hướng. Do đó, hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) không bằng nhau.
+ Hai vectơ \(\overrightarrow {AC} \) và \(\overrightarrow {BD} \) có cùng độ dài nhưng không cùng phương nên không cùng hướng. Do đó, hai vectơ \(\overrightarrow {CD} \) không bằng nhau.
Vậy trong các cặp vectơ đang xét, chỉ có cặp vectơ \(\overrightarrow {A{\rm{D}}} \) và \(\overrightarrow {BC} \) là bằng nhau \(\overrightarrow {A{\rm{D}}} = \overrightarrow {BC} \)
Nhận xét: Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi \(\overrightarrow {AB} ,\overrightarrow {AC} \) cùng phương.
Chú ý: Ta có thể dùng vectơ để biểu diễn các đại lượng như lực, vận tốc, gia tốc. Hướng của vectơ chỉ hướng của đại lượng, độ dài của vectơ thể hiện cho độ lớn của đại lượng và được lấy tỉ lệ với độ lớn của đại lượng.
Bài tập minh họa
Câu 1: Cho tam giác đều ABC với cạnh có độ dài bằng a. Hãy chỉ ra các vectơ có độ dài bằng a và có điểm đầu, điểm cuối là các đỉnh của tam giác ABC.
Hướng dẫn giải
Các vectơ có độ dài bằng a và có điểm đầu, điểm cuối là các đỉnh của tam giác ABC là:
\(\overrightarrow {AB} ;\;\overrightarrow {BA} ;\;\overrightarrow {AC} ;\;\overrightarrow {CA} ;\;\overrightarrow {BC} ;\;\overrightarrow {CB} \)
Chú ý khi giải:
Vectơ \(\overrightarrow {AB} \) khác vectơ \(\overrightarrow {BA} \) (khác nhau điểm đầu và điểm cuối).
Câu 2: Cho hình thang cân ABCD với hai đấy AB, CD, \(AB < CD\). Hãy chỉ ra mỗi quan hệ về đồ dài, phương, hướng giữa các cặp vectơ \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \), \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \), \(\overrightarrow {AC} \) và \(\overrightarrow {BD} \). Có cặp vectơ nào trong các cặp vectơ trên bằng nhau hay không?
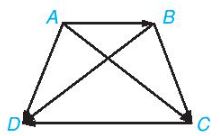
Hướng dẫn giải
Dễ thấy:
\(AD = BC\) nhưng \(AD\) và \(BC\) không song song với nhau. Do đó hai vectơ \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \) không bằng nhau.
\(CD > AB\) do đó hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) không bằng nhau.
\(AC\) và \(BD\) không song song với nhau. Do đó hai vectơ \(\overrightarrow {AC} \) và \(\overrightarrow {BD} \) không bằng nhau.
Câu 3: Xét các vectơ cùng phương trong hình cho sau. Hai vectơ \(\overrightarrow a \) và \(\overrightarrow {AB} \)được gọi là cùng hướng, còn hai vectơ \(\overrightarrow a \) và \(\overrightarrow x \) được gọi là ngược hướng. Hãy chỉ ra các vectơ cùng hướng với vectơ \(\overrightarrow a \) và các vectơ ngược hướng với vectơ \(\overrightarrow a \).
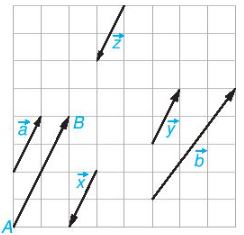
Hướng dẫn giải
Hai vectơ \(\overrightarrow a \) và \(\overrightarrow {AB} \) cùng hướng: có giá song song và cùng hướng với nhau.
Hai vectơ \(\overrightarrow a \) và \(\overrightarrow x \) ngược hướng: có giá song song và ngược hướng với nhau.
Vectơ \(\overrightarrow z \) có giá song song với giá của vectơ \(\overrightarrow a \), ngược hướng với vectơ \(\overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow z \) ngược hướng với nhau.
Vectơ \(\overrightarrow y \) có giá song song với giá của vectơ \(\overrightarrow a \), cùng hướng với vectơ \(\overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow y \) cùng hướng với nhau.
Vectơ \(\overrightarrow b \) có giá không song song với giá của vectơ \(\overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) không cùng phương với nhuau. Do vậy không xét chúng cùng hướng hay ngược hướng với nhau.
=============
– Học Toán lớp 10 – Kết nối
