TÌM TẬP HỢP ĐIỂM THỎA MÃN ĐẲNG THỨC VỀ TÍCH VÔ HƯỚNG HOẶC TÍCH ĐỘ DÀI

DẠNG TOÁN 3: TÌM TẬP HỢP ĐIỂM THỎA MÃN ĐẲNG THỨC VỀ TÍCH VÔ HƯỚNG HOẶC TÍCH ĐỘ DÀI.
1. PHƯƠNG PHÁP GIẢI
Ta sử dụng các kết quả cơ bản sau:
Cho $A$, $B$ là các điểm cố định. $M$ là điểm di động.
+ Nếu $|\overrightarrow {AM} | = k$ với $k$ là số thực dương cho trước thì tập hợp các điểm $M$ là đường tròn tâm $A$, bán kính $R = k.$
+ Nếu $\overrightarrow {MA} .\overrightarrow {MB} = 0$ thì tập hợp các điểm $M$ là đường tròn đường kính $AB.$
+ Nếu $\overrightarrow {MA} .\overrightarrow a = 0$ với $\overrightarrow a $ khác $\vec 0$ cho trước thì tập hợp các điểm $M$ là đường thẳng đi qua $A$ và vuông góc với giá của vectơ $\overrightarrow a .$

2. CÁC VÍ DỤ
Ví dụ 1 . Cho hai điểm $A$, $B$ cố định có độ dài bằng $a$, vectơ $\vec a$ khác $\vec 0$ và số thực $k$ cho trước. Tìm tập hợp điểm $M$ sao cho:
a) $\overrightarrow {MA} .\overrightarrow {MB} = \frac{{3{a^2}}}{4}.$
b) $\overrightarrow {MA} .\overrightarrow {MB} = M{A^2}.$

a) Gọi $I$ là trung điểm của $AB$ ta có:
$\overrightarrow {MA} .\overrightarrow {MB} = \frac{{3{a^2}}}{4}$ $ \Leftrightarrow (\overrightarrow {MI} + \overrightarrow {IA} )(\overrightarrow {MI} + \overrightarrow {IB} ) = \frac{{3{a^2}}}{4}.$
$ \Leftrightarrow M{I^2} – I{A^2} = \frac{{3{a^2}}}{4}$ (do $\overrightarrow {IB} = – \overrightarrow {IA} $).
$ \Leftrightarrow M{I^2} = \frac{{{a^2}}}{4} + \frac{{3{a^2}}}{4}$ $ \Leftrightarrow MI = a.$
Vậy tập hợp điểm $M$ là đường tròn tâm $I$ bán kính $R = a.$
b) Ta có $\overrightarrow {MA} .\overrightarrow {MB} = M{A^2}$ $ \Leftrightarrow \overrightarrow {MA} .\overrightarrow {MB} = {\overrightarrow {MA} ^2}.$
$ \Leftrightarrow \overrightarrow {MA} .(\overrightarrow {MA} – \overrightarrow {MB} ) = 0$ $ \Leftrightarrow \overrightarrow {MA} .\overrightarrow {BA} = 0$ $ \Leftrightarrow \overrightarrow {MA} \bot \overrightarrow {BA} .$
Vậy tập hợp điểm $M$ là đường thẳng vuông góc với đường thẳng $AB$ tại $A.$

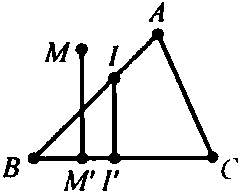
Ví dụ 2 : Cho tam giác $ABC.$ Tìm tập hợp điểm $M$ sao cho $(\overrightarrow {MA} + 2\overrightarrow {MB} + 3\overrightarrow {CB} )\overrightarrow {BC} = 0.$

Gọi $I$ là điểm xác định bởi $\overrightarrow {IA} + 2\overrightarrow {IB} = \vec 0.$
Khi đó $(\overrightarrow {MA} + 2\overrightarrow {MB} + 3\overrightarrow {CB} )\overrightarrow {BC} = 0.$
$ \Leftrightarrow \left[ {(\overrightarrow {MI} + \overrightarrow {IA} ) + 2(\overrightarrow {MI} + \overrightarrow {IB} )} \right].\overrightarrow {BC} $ $ = 3B{C^2}.$
$ \Leftrightarrow \overrightarrow {MI} .\overrightarrow {BC} = B{C^2}.$
Gọi $M’$, $I’$ lần lượt là hình chiếu của $M$, $I$ lên đường thẳng $BC.$
Theo công thức hình chiếu ta có $\overrightarrow {MI} .\overrightarrow {BC} = \overrightarrow {M’I’} .\overrightarrow {BC} $, do đó $\overrightarrow {M’I’} .\overrightarrow {BC} = B{C^2}.$
Vì $B{C^2} > 0$ nên $\overrightarrow {M’I’} $, $\overrightarrow {BC} $ cùng hướng suy ra:
$\overrightarrow {M’I’} .\overrightarrow {BC} = B{C^2}$ $ \Leftrightarrow M’I’.BC = B{C^2}$ $ \Leftrightarrow M’I’ = BC.$
Do $I$ cố định nên $I’$ cố định suy ra $M’$ cố định.
Vậy tập hợp điểm $M$ là đường thẳng đi qua $M’$ và vuông góc với $BC.$

Ví dụ 3 : Cho hình vuông $ABCD$ cạnh $a$ và số thực $k$ cho trước. Tìm tập hợp điểm $M$ sao cho $\overrightarrow {MA} .\overrightarrow {MC} + \overrightarrow {MB} .\overrightarrow {MD} = k.$

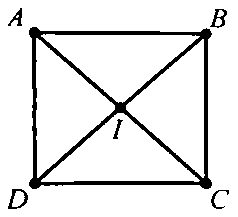
Gọi $I$ là tâm của hình vuông $ABCD.$
Ta có: $\overrightarrow {MA} .\overrightarrow {MC} $ $ = (\overrightarrow {MI} + \overrightarrow {IA} )(\overrightarrow {MI} + \overrightarrow {IC} )$ $ = M{I^2} + \overrightarrow {MI} (\overrightarrow {IC} + \overrightarrow {IA} ) + \overrightarrow {IA} .\overrightarrow {IC} $ $ = M{I^2} + \overrightarrow {IA} .\overrightarrow {IC} .$
Tương tự $\overrightarrow {MB} .\overrightarrow {MD} = M{I^2} + \overrightarrow {IB} .\overrightarrow {ID} .$
Nên $\overrightarrow {MA} .\overrightarrow {MC} + \overrightarrow {MB} .\overrightarrow {MD} = k$ $ \Leftrightarrow 2M{I^2} + \overrightarrow {IB} .\overrightarrow {ID} + \overrightarrow {IA} .\overrightarrow {IC} = k.$
$ \Leftrightarrow 2M{I^2} – I{B^2} – I{A^2} = k$ $ \Leftrightarrow M{I^2} = \frac{k}{2} + I{A^2}$ $ \Leftrightarrow M{I^2} = \frac{k}{2} + {a^2}.$
$ \Leftrightarrow MI = \sqrt {\frac{k}{2} + I{A^2}} $ $ = \sqrt {\frac{{k + {a^2}}}{2}} .$
Nếu $k < – {a^2}$: Tập hợp điểm $M$ là tập rỗng.
Nếu $k = – {a^2}$ thì $MI = 0$ $ \Leftrightarrow M \equiv I$ suy ra tập hợp điểm $M$ là điểm $I.$
Nếu $k > – {a^2}$ thì $MI = \sqrt {\frac{{k + {a^2}}}{2}} .$
Suy ra tập hợp điểm $M$ là đường tròn tâm $I$ bán kính $R = \sqrt {\frac{{k + {a^2}}}{2}} .$