1. Các định nghĩa
+ Vectơ là một đoạn thẳng có hướng. Kí hiệu vectơ có điểm đầu $A,$ điểm cuối $B$ là \(\overrightarrow {AB} \).
+ Giá của vectơ là đường thẳng chứa vectơ đó.
+ Độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối của vectơ, kí hiệu \(\left| {\overrightarrow {AB} } \right|\).
+ Vectơ – không là vectơ có điểm đầu và điểm cuối trùng nhau, kí hiệu \(\vec 0\).
+ Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
+ Hai vectơ cùng phương có thể cùng hướng hoặc ngược hướng .
+ Hai vectơ được gọi là bằng nhau nếu chúng cùng hướng và có cùng độ dài.
Chú ý:
+) Ta còn sử dụng kí hiệu \(\vec a,\,\,\vec b,\,…\) để biểu diễn vectơ.
+) Qui ước: Vectơ \(\vec 0\) cùng phương, cùng hướng với mọi vectơ.
+) Mọi vectơ \(\vec 0\) đều bằng nhau.
2. Tổng, hiệu hai véc tơ
a. Tổng của hai vectơ
+) Qui tắc ba điểm: Với ba điểm $A,B,C$ tuỳ ý, ta có: \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \).
+) Qui tắc hình bình hành: Với $ABCD$ là hình bình hành, ta có: \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \).
+) Tính chất: \(\vec a + \vec b = \vec b + \vec a\);\(\left( {\vec a + \vec b} \right) + \vec c = \vec a + \left( {\vec b + \vec c} \right)\);\(\vec a + \vec 0 = \vec a\)
b. Hiệu của hai vectơ
+) Vectơ đối của \(\vec a\) là vectơ \(\vec b\) sao cho \(\vec a + \vec b = \vec 0\). Kí hiệu vectơ đối của \(\vec a\) là \( – \vec a\).
+) Vectơ đối của \(\vec 0\) là \(\vec 0\).
+) \(\vec a – \vec b = \vec a + \left( { – \vec b} \right)\).
3. Tích của một véc tơ với một số
*) Cho vectơ \(\vec a\) và số $k \in R.$ \(k\vec a\) là một vectơ được xác định như sau:
+ \(k\vec a\) cùng hướng với \(\vec a\) nếu $k \ge 0,$ \(k\vec a\) ngược hướng với \(\vec a\) nếu $k < 0.$
+ \(\left| {k\vec a} \right| = \left| k \right|.\left| {\vec a} \right|\)
*) Tính chất
\(k\left( {\vec a + \vec b} \right) = k\vec a + k\vec b\);
\((k + l)\vec a = k\vec a + l\vec a\);
\(k\left( {l\vec a} \right) = (kl)\vec a\)
\(k\vec a = \vec 0\) $ \Leftrightarrow k = 0$ hoặc \(\vec a = \vec 0\).
*) Điều kiện để hai vectơ cùng phương
\(\vec a\) và \(\vec b\left( { \ne \vec 0} \right)\) cùng phương \( \Leftrightarrow \exists k \in \mathbb{R}:\vec b = k\vec a\)
*) Điều kiện ba điểm thẳng hàng
$A,B,C$ thẳng hàng \( \Leftrightarrow k \ne 0:\overrightarrow {AB} = k\overrightarrow {AC} \).
*) Biểu thị một vectơ theo hai vectơ không cùng phương
Cho hai vectơ không cùng phương \(\vec a,\,\vec b\) và \(\vec x\) tuỳ ý. Khi đó \(\exists !m,n \in \mathbb{R}:\vec x = m\vec a + n\vec b\)
Chú ý:
+) Hệ thức trung điểm đoạn thẳng
$M$ là trung điểm của đoạn thẳng \(AB\) \( \Leftrightarrow \overrightarrow {MA} + \overrightarrow {MB} = \vec 0\) \( \Leftrightarrow \overrightarrow {OA} + \overrightarrow {OB} = 2\overrightarrow {OM} \) ($O$ tuỳ ý).
+) Hệ thức trọng tâm tam giác
$G$ là trọng tâm $ \Delta ABC$ $\Leftrightarrow$ \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \vec 0\) \(\Leftrightarrow \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 3\overrightarrow {OG} \) ($O$ tuỳ ý).
4. Hệ trục tọa độ
a. Tọa độ điểm
Trong hệ trục tọa độ \(\left( {O;\overrightarrow i ,\overrightarrow j } \right)\), tọa độ của vectơ \(\overrightarrow {OM} \) gọi là tọa độ của điểm $M,$ kí hiệu là \(M = \left( {x;y} \right)\) hay \(M\left( {x;y} \right)\). $x$ được gọi là hoành độ, $y$ được gọi là tung độ của điểm $M.$
Tọa độ trung điểm, trọng tâm tam giác
+ Cho \(A({x_A};{y_A}),{\rm{ }}B({x_B};{y_B})\) và $M$ là trung điểm $AB.$ Tọa độ trung điểm \(M\left( {{x_M};{y_M}} \right)\) của đoạn thẳng AB là ${x_M} = \dfrac{{{x_A} + {x_B}}}{2},\,\,{y_M} = \dfrac{{{y_A} + {y_B}}}{2}$
+ Cho tam giác \(ABC\) có \(A({x_A};{y_A}),{\rm{ }}B({x_B};{y_B}),\,\,C\left( {{x_C};{y_C}} \right)\). Tọa độ trọng tâm \(G\left( {{x_G};{y_G}} \right)\) của tam giác \(ABC\) là ${x_G} = \dfrac{{{x_A} + {x_B} + {x_C}}}{3}$ và ${y_G} = \dfrac{{{y_A} + {y_B} + {y_C}}}{3}$
b. Biểu thứ tọa độ của các phép toán vectơ.
Cho $\overrightarrow u = (x;y)$ ;$\overrightarrow {u’} = (x’;y’)$ và số thực $k.$ Khi đó ta có :
1) \(\overrightarrow u = \overrightarrow {u’} \Leftrightarrow \left\{ \begin{array}{l}x = x’\\y = y’\end{array} \right.\)
2) $\overrightarrow u \pm \overrightarrow v = (x \pm x’;y \pm y’)$
3) $k.\overrightarrow u = (kx;ky)$
4) $\overrightarrow {u’} $ cùng phương $\overrightarrow u $($\overrightarrow u \ne \overrightarrow 0 $) khi và chỉ khi có số $k$ sao cho \(\left\{ \begin{array}{l}x’ = kx\\y’ = ky\end{array} \right.\)
5) Cho \(A({x_A};{y_A}),{\rm{ }}B({x_B};{y_B})\) thì \(\overrightarrow {AB} = \left( {{x_B} – {x_A};{y_B} – {y_A}} \right)\)
Bài tập trọng tâm
Bài 1:
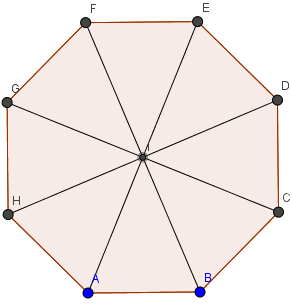
Cho bát giác đều ABCDEFGH tâm I. Các vectơ khác vectơ không, cùng phương với vectơ \(\vec{AB}\) và nhận các đỉnh của bát giác là gốc và ngọn là?

Hướng dẫn: Như bài toán đã nói rất rõ rằng tìm các vectơ cùng phương với vectơ \(\vec {AB}\).
Đầu tiên ta liệt kê các đoạn thẳng song song với AB, đó là đoạn EF, CH và GD.
Vậy ứng với các đoạn trên, ta có \(\vec {CH},\vec {HC},\vec {EF},\vec {FE},\vec {GD},\vec {DG},\vec {BA}\)
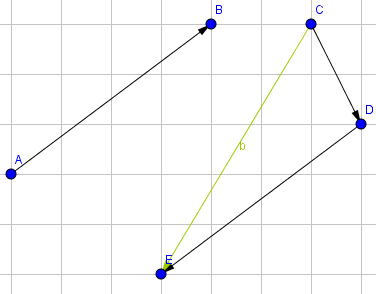
Bài 2: Hãy vẽ vectơ tổng của Vectơ \(\vec {AB}\&\vec {CD}\)và hiệu của 2 vectơ \(\vec {CD\&}\vec {AB}\) sau:
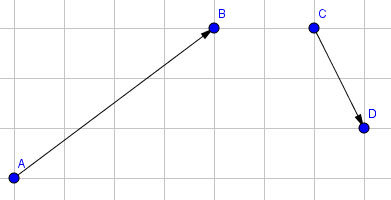
Hướng dẫn: Giả sử độ dài đơn vị tính bằng ô, ta có:
Tổng hai vectơ \(\vec {AB}\&\vec {CD}\) trên là vectơ \(\vec {a}\)
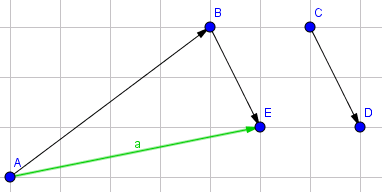
Hiệu hai vectơ \(\vec {CD\&}\vec {AB}\) trên là \(\vec {b}\)
Bài 3:
Cho hình chữ nhật có \(AB=3cm\), \(BC=4cm\). Tính \(|\vec{AB}+2\vec{AC}-\vec{AD}|\)
Hướng dẫn:
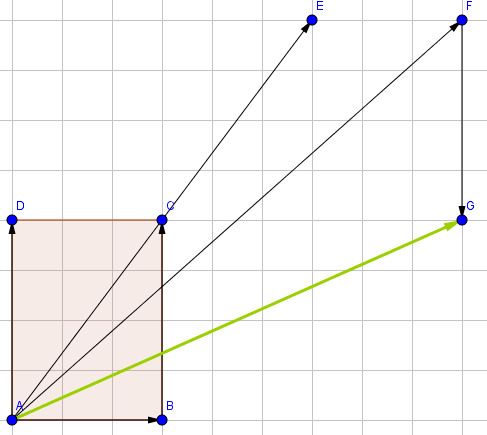
Như hình trên, chúng ta có thể viết lại như sau:
\(2\vec{AC}=\vec{AE}\)
\(-\vec{AD}=\vec{DA}=\vec{EG}\)
\(\vec{AB}=\vec{EF}\)
Vậy \(\vec{AB}+2\vec{AC}-\vec{AD}=\vec{AG}\)
Bằng Pytago, ta dễ dàng tính toán được \(|\vec{AG}|=\sqrt{97}(cm)\)
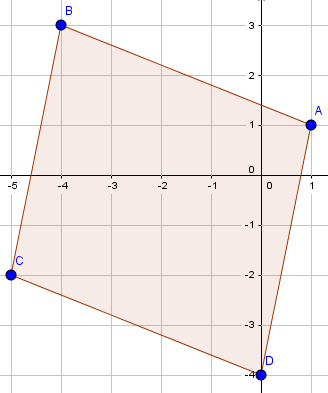
Bài 4: Trong mặt phẳng tọa độ. Cho 3 điểm \(A(1;1); B(-4;3);C(-5;-2)\).
Tìm tọa độ đỉnh D sao cho ABCD là hình bình hành
Hướng dẫn:
ABCD là hình bình hành, suy ra \(\vec{AB}=\vec{DC}\)
Mà \(\vec{AB}=(-4-1;3-1)\Leftrightarrow \vec{AB}=(-5;2)\)
Suy ra \(\left\{\begin{matrix} x_D=-5+5\\ y_D=-2-2 \end{matrix}\right.\)
Vậy \(D(0;-4)\)