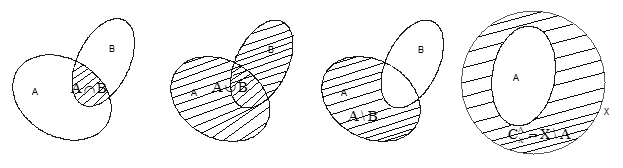
LÝ THUYẾT
1. Phép giao
$A \cap B = {\rm{\{ }}x \in A$ và \(x \in B{\rm{\} }}\) hay \(x \in A \cap B \Leftrightarrow \left\{ \begin{array}{l}x \in A\\x \in B\end{array} \right.\)
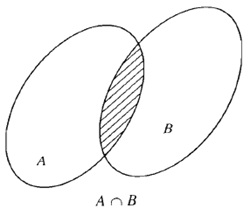
Ví dụ: Cho tập \(A = \left\{ {1;4;3} \right\},B = \left\{ {1;2} \right\}\) thì \(A \cap B = \left\{ 1 \right\}\)
2. Phép hợp
\(A \cup B = \left\{ {x|x \in A\,{\rm{hay }}x \in B} \right\}\) hay \(x \in A \cup B \Leftrightarrow \left[ \begin{array}{l}x \in A\\x \in B\end{array} \right.\)
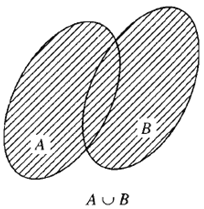
Ví dụ: Cho tập \(A = \left\{ {1;4;3} \right\},B = \left\{ {1;2} \right\}\) thì \(A \cup B = \left\{ {1;2;3;4} \right\}\)
3. Hiệu của hai tập hợp
\(A\backslash B = {\rm{\{ x}} \in {\rm{A}}\) và \(x \notin B{\rm{\} }}\) hay \(x \in A\backslash B \Leftrightarrow \left\{ \begin{array}{l}x \in A\\x \notin B\end{array} \right.\)
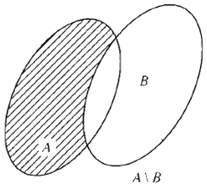
Ví dụ: Cho tập \(A = \left\{ {1;4;3} \right\},B = \left\{ {1;2} \right\}\) thì \(A\backslash B = \left\{ {3;4} \right\}\) và \(B\backslash A = \left\{ 2 \right\}\)
\(A\backslash B \subset A,B\backslash A \subset B\)
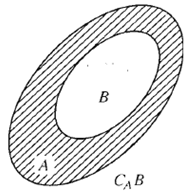
4. Phần bù
Cho tập \(A \subset X\), khi đó phần bù của \(A\) trong \(X\) là \(X\backslash A\), kí hiệu là \({C_X}A\).
Vậy \({C_X}A = X\backslash A = {\rm{\{ }}x|x \in X\) và \(x \notin A{\rm{\} }}\)
VÍ DỤ VẬN DỤNG
Ví dụ 1:
Cho tập \(A = \left\{ {1;4;3} \right\},B = \left\{ {1;3} \right\}\) thì \({C_A}B = A\backslash B = \left\{ 4 \right\}\)

Ví dụ 2:
Cho \(A = \left\{ {1;2;3;5;6} \right\};\,B = \left\{ {x \in \mathbb{Z}| – 3 \le x \le 2} \right\}\)
\(C = \left\{ {x \in \mathbb{R}|2{x^2} – 3x = 0} \right\}\)
a) Dừng phương pháp liệt kê phần tử xác định các tập hợp B và C.
b) Xác định các tập hợp sau: \(A \cap B,B \cap C,A \cap C.\)
c) Xác định các tập hợp sau: \(A \cup B,B \cup C,A \cup C.\)
d) Xác định các tập hợp sau: \(A\backslash B,B\backslash C,A\backslash C.\)
Hướng dẫn giải:
a) \(B = \left\{ { – 3; – 2; – 1;0;1;2} \right\};\,\,C = \left\{ {0;\frac{3}{2}} \right\}.\)
b) \(A \cap B = \left\{ {1;2} \right\};B \cap C = \left\{ 0 \right\};A \cap C = \emptyset .\)
c) \(A \cup B = \left\{ { – 3; – 2; – 1;0;1;2;3;4;5;6} \right\}.\)
\(B \cup C = \left\{ { – 3; – 2; – 1;0;1;2;\frac{3}{2}} \right\}\)
\(A \cup C = \left\{ {0;1;2;3;4;5;6;\frac{3}{2}} \right\}\)
d) \(A\backslash B = \left\{ {3;4;5;6} \right\};\,\,B\backslash C = \left\{ { – 3; – 2; – 1;1;2} \right\};\)
\(A\backslash C = \left\{ {1;2;3;4;5;6} \right\}.\)
Ví dụ 3:
Cho \(A = \left\{ {0;2;4;6;8;10} \right\};B = {\rm{\{ }}0;1;2;3;4;5;6\} ;C = \left\{ {4;5;6;7;8;9;10} \right\}.\)
Hãy liệt kê các phần tử của các tập hợp dưới đây?
a) \(A \cap (B \cap C);\)
b) \(A \cup (B \cup C);\)
c) \(A \cap \left( {B \cup C} \right);\)
d) \(A \cup (B \cap C).\)
e) \(\left( {A \cap B} \right) \cup C.\)
Hướng dẫn giải:
a) Ta có: \(B \cap C = \left\{ {4;5;6} \right\}\)
\( \Rightarrow A \cap \left( {B \cap C} \right) = \left\{ {4;6} \right\}.\)
b) \(B \cup C = \left\{ {0;1;2;3;4;5;6;7;8;9;10} \right\}\)
\( \Rightarrow A \cup \left( {B \cup C} \right) = \left\{ {0;1;2;3;4;5;6;7;8;9;10} \right\}.\)
c) Ta có \(B \cup C = \left\{ {0;1;2;3;4;5;6;7;8;9;10} \right\}\)
\( \Rightarrow A \cap \left( {B \cup C} \right) = \left\{ {0;2;4;6;8;10} \right\}.\)
d) Ta có: \(B \cap C = \left\{ {4;5;6} \right\}\)
\( \Rightarrow A \cup (B \cap C) = \left\{ {0;2;4;5;6;8;10} \right\}.\)
e) Ta có: \(A \cap B = \left\{ {0;2;4;6} \right\}\)
\( \Rightarrow \left( {A \cap B} \right) \cup C = \left\{ {2;4;5;6;7;8;9;10} \right\}.\)
Ví dụ 4: Liệt kê các phần tử của tập hợp \(X=\left\{ x\in \mathbb{R}\left| 2{{x}^{2}}-7x+5=0 \right. \right\}.\)
A. \(X=\left\{ 1;\frac{5}{2} \right\}\).
B. \(X=\left\{ 1 \right\}\).
C. \(X=\left\{ -1;\frac{5}{2} \right\}\).
D. \(X=\varnothing \).
Lời giải
Chọn A.
Cách 1: Giải phương trình \(2{x^2} – 7x + 5 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 1}\\ {x = \frac{5}{2}} \end{array}} \right.\). Hai nghiệm này đều thuộc \(\mathbb{R}\).
Cách 2: Nhập vào máy tính \(2{{X}^{2}}-7X+5=0\) sau đó ấn Calc lần lượt các đáp án, đáp án câu nào làm phương trình bằng 0 thì chọn đáp án đó.
Ví dụ 5: Liệt kê các phần tử của tập hợp \(X=\left\{ x\in \mathbb{N}\left| 3x-5
A. \(X=\left\{ 1;2;3 \right\}\).
B. \(X=\left\{ 1,2 \right\}\).
C. \(X=\left\{ 0;1;2 \right\}\).
D. \(X=\varnothing \).
Lời giải
Chọn C.
Cách 1: Giải bất phương trình \(3x-5<x\leftrightarrow c=”” leftrightarrow=”” n=”” p=”” u=””></x\leftrightarrow>
Cách 2: Nhận xét các phần tử ở các đáp án A, B, C lần lượt thay các phần tử ở các đáp án thế vào bất phương trình, tất cả các phần tử của đáp án nào thỏa yêu cầu bài toán thì ta sẽ chọn.
Ví dụ 6: Liệt kê các phần tử của tập hợp \(X=\left\{ x\in \mathbb{N}\left| \frac{5}{\left| 2x-1 \right|}>2 \right. \right\}.\)
A. \(X=\left\{ 0;1;2;3 \right\}\).
B. \(X=\left\{ 0;1 \right\}\).
C. \(X=\left\{ 0;1;2 \right\}\).
D. \(X=\varnothing \).
Lời giải
Chọn B.
Cách 1: Giải bất phương trình \(\left| {2x – 1} \right| < \frac{5}{2} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {2x – 1 < \frac{5}{2}}\\ {2x – 1 > – \frac{5}{2}} \end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {x < \frac{7}{4}}\\ {x > \frac{{ – 3}}{4}} \end{array}} \right..\)
Mà \(x\) là các số tự nhiên nên chọn câu B.
Cách 2: Nhận xét các phần tử ở các đáp án A, B, C lần lượt thay các phần tử ở các đáp án thế vào bất phương trình, tất cả các phần tử của đáp án nào thỏa yêu cầu bài toán thì ta sẽ chọn.
Ví dụ 7: Liệt kê các phần tử của tập hợp \(X=\left\{ x\in \mathbb{Z}\left| ({{x}^{2}}-10x+21)({{x}^{3}}-x)=0 \right. \right\}\)
A. \(X=\left\{ 0;1;2;3 \right\}\).
B. \(X=\left\{ 0;1;3;7 \right\}\).
C. \(X=\varnothing .\)
D. \(X=\left\{ -1;0;1;3;7 \right\}\).
Lời giải
Chọn D.
Cách 1: Giải phương trình \(({x^2} – 10x + 21)({x^3} – x) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {{x^2} – 10x + 21 = 0}\\ {{x^3} – x = 0} \end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {x = 3}\\ {x = 7} \end{array}} \right.}\\ {\left[ {\begin{array}{*{20}{c}} {x = 0}\\ {x = \pm 1} \end{array}} \right.} \end{array}} \right..\)
Mà \(x\) là các số nguyên nên chọn câu D.
Cách 2: Nhận xét các phần tử ở các đáp án A, B, C lần lượt thay các phần tử ở các đáp án thế vào bất phương trình, tất cả các phần tử của đáp án nào thỏa yêu cầu bài toán thì ta sẽ chọn.
