I. MỆNH ĐỀ
1. Định nghĩa
Mệnh đề là một câu khẳng định Đúng hoặc Sai .
Một mệnh đề không thể vừa đúng hoặc vừa sai
2. Mệnh đề phủ định
Cho mệnh đề \(P\). Mệnh đề “Không phải \(P\) ” gọi là mệnh đề phủ định của \(P\).
Ký hiệu là $\overline P $. Nếu P đúng thì $\overline P $ sai, nếu \(P\) sai thì $\overline P $ đúng
3. Mệnh đề kéo theo và mệnh đề đảo
Cho hai mệnh đề \(P\) và \(Q\). Mệnh đề “nếu \(P\) thì \(Q\)” gọi là mệnh đề kéo theo
Ký hiệu là \(P \Rightarrow Q\). Mệnh đề \(P \Rightarrow Q\) chỉ sai khi P đúng Q sai
Cho mệnh đề \(P \Rightarrow Q\). Khi đó mệnh đề \(Q \Rightarrow P\) gọi là mệnh đề đảo của \(Q \Rightarrow P\)
4. Mệnh đề tương đương
Cho hai mệnh đề \(P\) và \(Q\). Mệnh đề “\(P\) nếu và chỉ nếu \(Q\)” gọi là mệnh đề tương đương
Ký hiệu là \(P \Leftrightarrow Q\).
Mệnh đề \(P \Leftrightarrow Q\) đúng khi cả \(P \Rightarrow Q\) và \(Q \Rightarrow P\) cùng đúng
Chú ý: “Tương đương” còn được gọi bằng các thuật ngữ khác như “điều kiện cần và đủ”, “khi và chỉ khi”, “nếu và chỉ nếu”.
5. Mệnh đề chứa biến
Mệnh đề chứa biến là một câu khẳng định chứa biến nhận giá trị trong một tập \(X\) nào đó mà với mỗi giá trị của biến thuộc $X$ ta được một mệnh đề.
Ví dụ: \(P\left( n \right):\) “\(n\) chia hết cho \(5\)” với \(n\) là số tự nhiên
\(P\left( {x;y} \right)\) :”\(2x + y = 5\)” Với \(x,y\) là số thực
6. Các kí hiệu \(\forall \), \(\exists \) và mệnh đề phủ định của mệnh đề có chứa kí hiệu \(\forall \),\(\exists \)
Kí hiệu $\forall$ đọc là với mọi, $\exists$ đọc là tồn tại
Phủ định của mệnh đề “$\forall x \in X,P\left( x \right)$ ” là mệnh đề “$\exists x \in X,\overline {P(x)} $”
Phủ định của mệnh đề “$\exists x \in X,P\left( x \right)$ ” là mệnh đề “$\forall x \in X,\overline {P(x)} $”
II. TẬP HỢP
1. Định nghĩa
Là một nhóm các phần tử có cùng tính chất hoặc có cùng một đặc điểm nào đó. Tập hợp thường được kí hiệu bằng chữ cái in hoa như: $A,B,C, \ldots $
2. Các xác định tập hợp
Có $2$ cách để xác định tập hợp
a) Liệt kê: Viết tất cả các phần tử của tập hợp vào giữa dấu \(\left\{ {} \right\}\), các phần tử cách nhau bởi dấu \(”,”\) đối với tập hợp gồm các phần tử là chữ, hoặc \(”;”\) đối với tập hợp có các phần tử là số.
b) Nêu tính chất đặc trưng: Chỉ ra tính chất đặc trưng của các phần tử.
3. Tập hợp rỗng
Là tập hợp không chứa phần tử nào, kí hiệu là \(\emptyset \).
\(A \ne \emptyset \Leftrightarrow \exists x:x \in A\)
Tập hợp $A$ là con của tập hợp $B$ hay còn gọi tập $B$ là tập cha của tập $A.$ Kí hiệu: \(A \subset B\).
\(A \subset B \Leftrightarrow \left( {\forall x \in A \Rightarrow x \in B} \right)\)
Chú ý:
+) \(\emptyset \subset A,\forall A\)
+) ${\rm{A}} \subset {\rm{A,}}\forall {\rm{A}}$
+) $A \subset B,B \subset C \Rightarrow A \subset C$ (bắc cầu).
+) Số tập con của một tập hợp: Tập hợp $A$ gồm có $n$ phần tử thì số tập con (chứa cả \(\emptyset \) và \(A\)) của tập hợp $A$ là \(P\left( A \right) = {2^n}\).
+) Số phần tử của một tập hợp \(A\) là \(n(A)\) hoặc \(\left| A \right|\)
4. Hai tập hợp bằng nhau
\(A = B \Leftrightarrow \forall x,\left( {x \in A \Leftrightarrow x \in B} \right) \Leftrightarrow \left\{ \begin{array}{l}A \subset B\\B \subset A\end{array} \right.\)
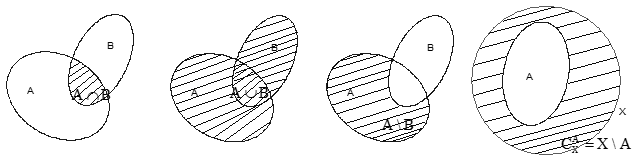
5. Các phép toán trên tập hợp
a. Phép giao : $A \cap B = \left\{ {x|x \in A} \right.$ và $\left. {x \in B} \right\}$ hay \(x \in A \cap B \Leftrightarrow \left\{ \begin{array}{l}x \in A\\x \in B\end{array} \right.\)
b. Phép hợp: $A \cup B = \left\{ {x|x \in A} \right.$ hoặc $\left. {x \in B} \right\}$ hay \(x \in A \cup B \Leftrightarrow \left[ \begin{array}{l}x \in A\\x \in B\end{array} \right.\)
c . Hiệu của hai tập hợp: \(A\backslash B = \left\{ {x\left| {x \in A} \right.} \right.\) và \(\left. {x \notin B} \right\}\) hay \(x \in A\backslash B \Leftrightarrow \left\{ \begin{array}{l}x \in A\\x \notin B\end{array} \right.\)
d . Phần bù: Cho tập \(A \subset X\), khi đó phần bù của \(A\) trong \(X\) là \(X\backslash A\), kí hiệu là \({C_X}A\).
Vậy \({C_X}A = X\backslash A = \left\{ {x\left| {x \in X} \right.} \right.\) và \(\left. {x \notin A} \right\}\)

6. Các tập hợp số
a. Các tập hợp số thường gặp
\({\mathbb{N}^*} \subset \mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R}\)
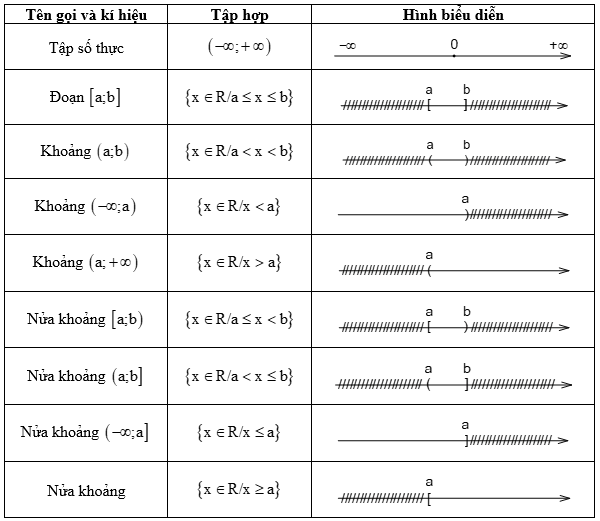
b. Các tập hợp con của \(\mathbb{R}\)
Bài tập minh họa
Bài 1:
Lập mệnh đề đảo của các định lí sau và cho biết mệnh đề này đúng hay sai. Viết mệnh đề tương đương (nếu được):
a) “Nếu a và b cùng chia hết cho c thì a + b chia hết cho c (a, b, c là những số nguyên)”.
b) “Nếu một số có tổng các chữ số chia hết cho 3 thì số đó chia hết cho 3”.
c) “Nếu tứ giác là hình vuông thì tứ giác có bốn cạnh bằng nhau”.
d) “Nếu \(\Delta ABC\) cân thì \(\Delta ABC\) có hai đường trung tuyến bằng nhau”.
Hướng dẫn giải:
a) Mệnh đề đảo: “Nếu a + b chia hết cho c thì a và b cùng chia hết cho c(a,b,c là các số nguyên)” là mệnh đề sai.
b) Mệnh đề đảo: “Nếu một số chia hết cho 3 thì số đó có tổng các chữ số chia hết cho 3” \( \to \) mệnh đề đúng.
Mệnh đề tương đương: “ Một số chia hết cho 3 khi và chỉ khi số đó có tổng các chữ số chia hết cho 3”.
c) Mệnh đề đảo: “ Nếu tứ giác có 4 cạnh bằng nhau thì tư giác đó là hình vuông” \( \to \) mệnh đề sai.
d) Mệnh đề đảo:” Nếu \(\Delta ABC\) có hai đường trung tuyến bằng nhau thì \(\Delta ABC\) là tam giác cân” \( \to \) mệnh đề đúng.
Mệnh đề tương đương: “\(\Delta ABC\) có hai đường trung tuyến bằng nhau khi và chỉ khi \(\Delta ABC\) là tam giác cân”.
Bài 2:
Cho các tập hợp \(A = \left[ { – 3;2} \right),\;B = \left( { – 2;4} \right],\;C = \left( { – \infty ;3} \right),\;D = \left[ {1; + \infty } \right).\)
Hãy xác định các tập hợp sau:
a) \(A \cap B\)
b) \(A \cup B\)
c) \(\mathbb{R}\backslash C\)
d) \(D\backslash \left( {A \cup B} \right)\)
Hướng dẫn giải:
a) \(A \cap B = ( – 2;\,2)\).
b) \(A \cup B = \left[ { – 3;\,4} \right]\).
c) \(\mathbb{R}\backslash C = \left[ {3;\, + \infty } \right)\).
d) \(D\backslash (A \cup B) = \left[ {1;\, + \infty } \right)\backslash \left[ { – 3;\,4} \right] = \left( {4;\, + \infty } \right)\).
Bài 3:
Cho tập hợp \(A = \left\{ {x \in \mathbb{R}|\,{x^2} – 2x + m – 1 = 0\,\,,\,m\, \in \mathbb{N}} \right\}\)
Tìm tất cả các giá trị của \(m\)để \(A \ne \emptyset \).
Hướng dẫn giải:
\(A \ne \emptyset \,\)khi phương trình \({x^2} – 2x + m – 1 = 0\) có nghiệm thực.
Điều nảy xảy ra khi \(\Delta ‘\, \ge \,0,\,m \in \mathbb{N}\)\( \Leftrightarrow 1 – (m – 1) \ge 0,\,m \in \mathbb{N}\)
\( \Leftrightarrow m \le 2,\,m \in \mathbb{N} \Leftrightarrow \,m = \left\{ {0\,;\,1\,;2} \right\}.\)
Vậy với \(m = \left\{ {0;\,1;2} \right\}\) thì \(A \ne \emptyset .\)
Bài 4:
a) Cho \(\sqrt 7 = 2,6457513…\) với độ chính xác là \(d = 0,003\). Hãy viết số quy tròn của số \(\sqrt 7 \)
b) Tìm hai số thực a và b để có \(\left\{ {x \in R|{x^3} – a{x^2} + bx + 12 = 0} \right.{\rm{\} }}\)=\(\left\{ { – 3;2} \right\}.\)
Hướng dẫn giải:
a) Do độ chính xác đến hàng phần nghìn nên ta quy tròn số hàng phần trăm nên Số quy tròn của\(\sqrt 7 \) là: 2,65.
b) Phương trình \({x^3} – a{x^2} + bx + 12 = 0\) có hai nghiệm là -3 và 2 nên ta có:
\(\left\{ \begin{array}{l} – 4a + 2b = – 20\\ – 9a – 3b = 15\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = – 8\end{array} \right..\)
Thử lại, giá trị a và b nhận được thỏa yêu cầu bài toán.
