Phân chia và lắp ghép khối đa diện
Việc phân chia và lắp ghép các khối đa diện thường được sử dụng để tính toán các yếu tố như thể tích, diện tích của những khối đa diện phức tạp. Có nhiều cách để phân chia một khối đa diện thành các khối đa diện khác như tứ diện, hình chóp,…
Phương pháp giải
Chọn mặt phẳng thích hợp để phân chia khối đa diện. Trong nhiều trường hợp, để chứng minh rằng có thể lắp ghép các khối đa diện (H1), (H2) … , (Hn) thành khối đa diện (H) ta chứng minh rằng có thể chia được khối đa diện (H) thành các khối đa diện (H1), (H2) … , (Hn).
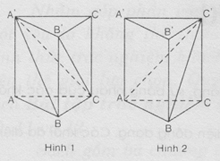
Ví dụ 1: Hình lăng trụ ABC.A’B’C’ có thế phân chia thành ba tứ diện như trong hình 1 ; phân chia thành một hình chóp tứ giác và một tứ diện như trong hình 2.

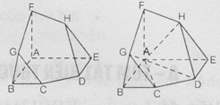
Ví dụ 2: Vì chỉ có thể tính thể tích một hình chóp nên để tính thể tích khối đa diện ABCDEHFG, ta chia khối đa diện này thành ba hình chóp: G.ABC ; H.ADE và A.CDHFG.
Ví dụ 3: Cho hình chóp tứ giác F.ABCD có đáy là hình vuông. Cạnh bên FC vuông góc với đáy và có độ dài bằng AB. Chứng minh rằng có thể dùng ba hình chóp bằng hình chóp trên để ghép lại thành một hình lập phương.
Giải
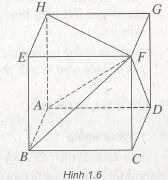
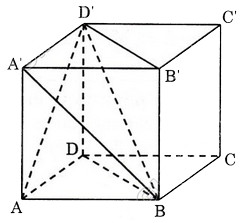
Từ hình chóp trên ta dựng hình lập phương HEFG.ABCD (h. 1.6). Ta thấy hai hình chóp
F.ABCD và F.ABEH đối xứng với nhau qua mặt phẳng (ABF), hai hình chóp F.ABCD và
F.AHGD đối xứng với nhau qua mặt phẳng (ADF). Do đó ba hình chóp F.ABCD, F.ABEH và
F.AHGD bằng nhau.
Như vậy có thể chia được hình lập phương HEFG.ABCD thành ba hình chóp bằng hình chóp
F.ABCD. Từ đó suy ra có thể ghép ba hình chóp bằng hình chóp F.ABCD để thành một hình
lập phương.
Ví dụ 4: Bài tập 3 trang 12 SGK Hình học 12
Chia một khối lập phương thành năm khối tứ diện.
Hướng dẫn giải chi tiết bài 3
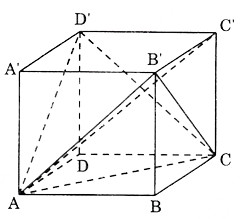
Chia khối lập phương ABCD.A’B’C’D’ thành năm khối tứ diện như sau:A’B’CD’, A’AB’D’, BACB’, C’B’CD’, DACD’.
—————-
Ví dụ 5: Bài tập 4 trang 12 SGK Hình học 12
Chia một khối lập phương thành sáu khối tứ diện bằng nhau.
Hướng dẫn giải chi tiết bài 4
Chia lăng trụ ABD.A’B’D’ thành ba tứ diện DABD’, A’ABD’, A’B’BD’. Phép đối xứng qua (ABD’) biến DABD’ thành A’ABD’, Phép đối xứng qua (BA’D’) biến A’ABD’ thành A’B’BD’ nên ba tứ diện DABA’, A’ABD’, A’B’BD’ bằng nhau
Làm tương tự đối với lăng trụ BCD.B’C’D’ ta sẽ chia được hình lập phương thành sáu tứ diện bằng nhau.
Xem video phân chia đa diện
