Khối đa diện là gì? (đọc thêm)
1. Hình đa diện (gọi tắt là đa diện) (H) là hình được tạo bởi một số hữu hạn các đa giác thỏa mãn hai điều kiện:
a) Hai đa giác phân biệt chỉ có thể hoặc không giao nhau, hoặc chỉ có một đỉnh chung, hoặc chỉ có một cạnh chung.
b) Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác.
Mỗi đa giác như thế được gọi là một mặt của hình đa diện (H). Các đỉnh, cạnh của các đa giác ấy theo thứ tự gọi là các đỉnh, cạnh của hình đa diện (H).

2. Phần không gian được giới hạn bới một hình đa diện (H) được gọi là khối đa diện (H).
3. Mỗi đa diện (H) chia các điểm còn lại của không gian thành hai miền không giao nhau: miền trong và miền ngoài của (H). Trong đó chỉ có duy nhất miền ngoài là chứa hoàn toàn một đường thẳng nào đấy.
Các điểm thuộc miền trong là các điểm trong, các điểm thuộc miền ngoài là các điểm ngoài của (H).
Khối đa diện (H) là hợp của hình đa diện (H) và miền trong của nó.
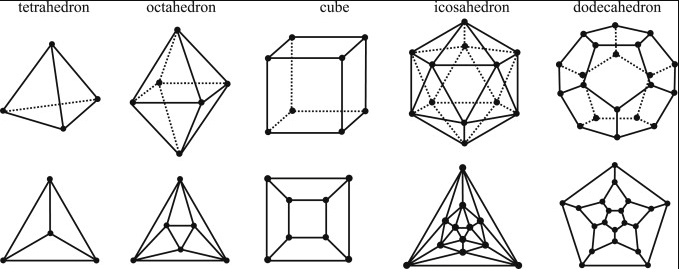
4. Phép dời hình và sự bằng nhau giữa các khối đa diện.
a) Trong không gian quy tắc đặt tương ứng mỗi điểm M với điểm M′ xác định duy nhất được gọi là một phép biến hình trong không gian.
b) Phép biến hình trong không gian được gọi là phép dời hình nếu nó bảo toàn khoảng cách giữa hai điểm tùy ý.
c) Thực hiện liên tiếp các phép dời hình sẽ được một phép dời hình.
d) Phép dời hình biến một đa diện thành một đa diện, biến các đỉnh, cạnh, mặt của đa diện này thành đỉnh, cạnh, mặt tương ứng của đa diện kia.
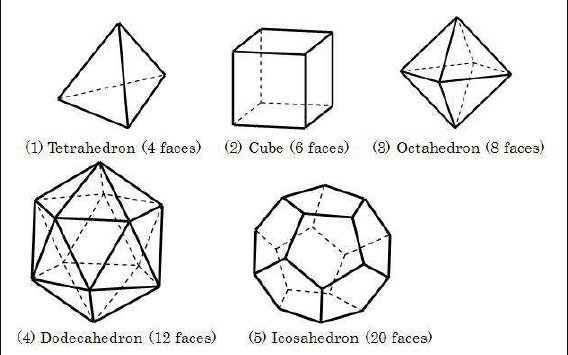
5. Nếu khối đa diện là hợp của hai khối đa diện sao cho và không có điểm trong chung thì ta nói có thể chia được khối đa diện thành hai khối đa diện và , hay có thể lắp ghép được hai khối đa diện và (H2) với nhau để được khối đa diện thành các khối tứ diện.
