Trong mặt phẳng tọa độ \(Oxy\), cho tam giác \(ABC\) vuông tại \(A\). Gọi \(H\) là hình chiếu vuông góc của \(A\)trên cạnh \(BC\); các điểm \(M\left( {6\,;\, – 1} \right)\), \(N\) lần lượt là trung điểm của \(HB\) và \(HC\); điểm \(K\left( {1\,;\,2} \right)\) là trực tâm tam giác \(AMN\). Tìm tọa độ đỉnh \(C\), biết \(A\) thuộc đường thẳng\(d:\,x + 2y + 4 = 0\) và có tung độ âm.

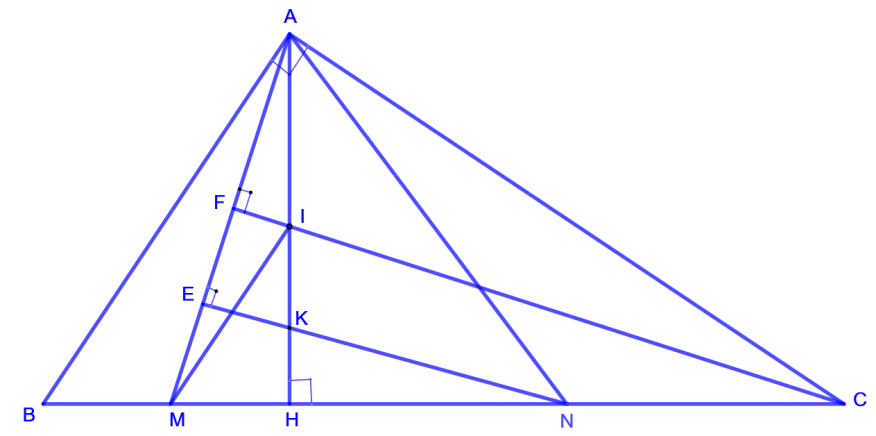
Trong mặt phẳng tọa độ \(Oxy\), cho tam giác \(ABC\) vuông tại \(A\). Gọi \(H\) là hình chiếu vuông góc của \(A\)trên cạnh \(BC\); các điểm \(M\left( {6\,;\, – 1} \right)\), \(N\) lần lượt là trung điểm của \(HB\)  và \(HC\); điểm \(K\left( {1\,;\,2} \right)\) là trực tâm tam giác \(AMN\). Tìm tọa độ đỉnh \(C\), biết \(A\) thuộc đường thẳng\(d:\,x + 2y + 4 = 0\) và có tung độ âm.

Lời giải

+ Gọi \(I\) là trung điểm của đoạn \(AH\), ta có \(MI\,//\,AB\) mà \(AB \bot AC\), suy ra \(MI \bot AC\).

Xét \(\Delta AMC\) có \(\left\{ \begin{array}{l}AI \bot MC\\MI \bot AC\end{array} \right.\) , suy ra \(I\)là trực tâm \(\Delta AMC\) \( \Rightarrow CI \bot AM\)  (1).

Theo bài ra, \(H\) là trực tâm tam giác \(AMN\) \( \Rightarrow NK \bot AM\) (2).

Từ (1) và (2), suy ra \(NK\,//\,CI\).

Xét tam giác \(IHM\) có \(NK\,//\,CI\) và \(N\)là trung điểm của \(HC\), suy ra \(K\) là trung điểm của \(HI\).

Ta có \(I\)là trung điểm của đoạn \(AH\) và \(K\) là trung điểm của đoạn \(HI\) \( \Rightarrow AK = 3KH\) (3).

+ Do \(A \in d:\,x + 2y + 4 = 0 \Rightarrow A\left( { – 4 – 2a\,;\,a} \right)\) với \(a < 0\). Khi đó \(\overrightarrow {AK}  = \left( {5 + 2a\,;\,2 – a} \right)\)

Theo (3), ta có  \(\overrightarrow {AK}  = 3\overrightarrow {KH}  \Rightarrow H\left( {\frac{{8 + 2a}}{3}\,\,;\,\frac{{8 – a}}{3}} \right)\)  và  \(\overrightarrow {MH}  = \left( {\frac{{2a – 10}}{3}\,;\,\frac{{11 – a}}{3}} \right)\).

Vì \(AK \bot MH \Rightarrow \overrightarrow {AK} .\overrightarrow {MH}  = 0\)\( \Leftrightarrow \left( {5 + 2a} \right).\frac{{2a – 10}}{3} + \left( {2 – a} \right).\frac{{11 – a}}{3} = 0\)

                                                 \( \Leftrightarrow 5{a^2} – 23a – 28 = 0 \Leftrightarrow \left[ \begin{array}{l}a =  – 1\\a = \frac{{28}}{5}\end{array} \right.\) , do  \(a < 0\) nên \(a =  – 1\).

Ta có  \(A\left( { – 2\,;\, – 1} \right)\) , \(H\left( {2\,;\,3} \right)\), \(I\) là trung điểm của đoạn \(AH \Rightarrow I\left( {0\,;\,1} \right)\).

+ Ta có \(MI \bot AC\), nên đường thẳng \(AC\) đi qua điểm \(A\left( { – 2\,;\, – 1} \right)\) và nhận véctơ \(\overrightarrow {IM}  = \left( {6\,;\, – 2} \right)\) làm một véctơ pháp tuyến. Phương trình đường thẳng \(AC:\,\,\,\,3x – y + 5 = 0\).

+ Đường thẳng \(BC\) đi qua hai điểm \(M\left( {6\,;\, – 1} \right)\) và \(H\left( {2\,;\,3} \right)\) có phương trình là \(x + y – 5 = 0\).

+ Ta có \(C = AC \cap BC\), nên tọa độ điểm \(C\) là nghiệm của hệ phương trình  \(\left\{ \begin{array}{l}3x – y + 5 = 0\\x + y – 5 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 0\\y = 5\end{array} \right.\) .

Vậy \(C\left( {0\,;\,5} \right)\).