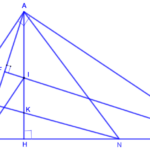
Trong mặt phẳng tọa độ \(Oxy\), cho tam giác \(ABC\) vuông tại \(A\). Gọi \(H\) là hình chiếu vuông góc của \(A\)trên cạnh \(BC\); các điểm \(M\left( {6\,;\, - 1} \right)\), \(N\) lần lượt là trung điểm của \(HB\) và \(HC\); điểm \(K\left( {1\,;\,2} \right)\) là trực tâm tam giác \(AMN\). Tìm tọa độ đỉnh \(C\), biết \(A\) thuộc đường thẳng\(d:\,x + 2y + 4 = 0\) và có tung … [Đọc thêm...] vềTrong mặt phẳng tọa độ \(Oxy\), cho tam giác \(ABC\) vuông tại \(A\). Gọi \(H\) là hình chiếu vuông góc của \(A\)trên cạnh \(BC\); các điểm \(M\left( {6\,;\, – 1} \right)\), \(N\) lần lượt là trung điểm của \(HB\) và \(HC\); điểm \(K\left( {1\,;\,2} \right)\) là trực tâm tam giác \(AMN\). Tìm tọa độ đỉnh \(C\), biết \(A\) thuộc đường thẳng\(d:\,x + 2y + 4 = 0\) và có tung độ âm.
Trong mặt phẳng tọa độ \(Oxy\), cho tam giác \(ABC\) vuông tại \(A\). Gọi \(H\) là hình chiếu vuông góc của \(A\)trên cạnh \(BC\); các điểm \(M\left( {6\,;\, – 1} \right)\), \(N\) lần lượt là trung điểm của \(HB\) và \(HC\); điểm \(K\left( {1\,;\,2} \right)\) là trực tâm tam giác \(AMN\). Tìm tọa độ đỉnh \(C\), biết \(A\) thuộc đường thẳng\(d:\,x + 2y + 4 = 0\) và có tung độ âm.
Ngày Thuộc chủ đề:Hình học OXY - Tự luận