Trả lời câu hỏi trong bài 4 Các số đặc trưng đo mức độ phân tán của mẫu số liệu – Chân trời

Trả lời câu hỏi trong bài 4 Các số đặc trưng đo mức độ phân tán của mẫu số liệu – Chân trời
============

KHỞI ĐỘNG

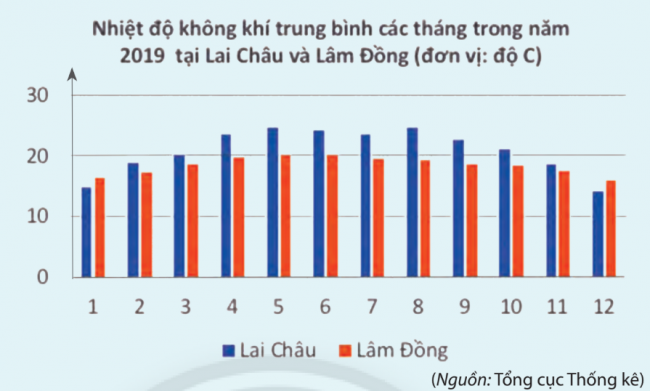
Theo bạn, địa phương nào có khí hậu ôn hòa hơn?

Hướng dẫn giải:

Lâm Đồng có khí hậu ôn hòa hơn.

1. KHOẢNG BIẾN THIÊN VÀ KHOẢNG TỨ PHÂN VỊ

Khám phá 1:  Thời gian hoàn thành bài chạy 5 km (tính theo phủ) của hai nhóm thanh niên được cho ở bảng sau:

a. Hãy tính độ chênh lệch giữa thời gian chạy của người nhanh nhất và người chậm nhất trong từng nhóm.

b. Nhóm nào có thành tích chạy đồng đều hơn?

Hướng dẫn giải:

a. Độ chênh lệch giữa thời gian chạy của người nhanh nhất và người chậm nhất trong nhóm 1 là: 47 – 17 = 30 (s)

    Độ chênh lệch giữa thời gian chạy của người nhanh nhất và người chậm nhất trong nhóm 2 là: 32 – 29 = 3 (s)

b. Nhóm 2 có thành tích chạy đồng đều hơn.

Thực hành 1:  Hãy tìm khoảng biến thiên và khoảng tứ phân vị của các mẫu số liệu sau:

a. 10; 13; 15; 2; 10; 19; 2; 5; 7                            b. 15; 19; 10; 5; 9; 10; 1; 2; 5; 15

Hướng dẫn giải:

a. Mẫu số liệu đã sắp xếp theo thứ tự không giảm là: 2; 2; 5; 7; 10; 10; 13; 15; 19.

• Khoảng biến thiên của mẫu số liệu là: R = 19 – 2 = 17.
• Cỡ mẫu n = 9 là số lẻ nên giá trị tứ phân vị thứ hai là $Q_{2}$ = 10.
• Tứ phân vị thứ nhất là trung vị của mẫu: 2; 2; 5; 7. Do đó $Q_{1}$ = $\frac{1}{2}$(2 + 5) = 3,5.
• Tứ phân vị thứ ba là trung vị của mẫu: 10; 13; 15; 19. Do đó $Q_{3}$ = $\frac{1}{2}$(13 + 15) = 14.
• Khoảng tứ phân vị của mẫu là: $\Delta_{Q}$ = 14 – 3,5 = 10,5.

b. Mẫu số liệu đã sắp xếp theo thứ tự không giảm là: 1; 2; 5; 5; 9; 10; 10; 15; 15; 19.

• Khoảng biến thiên của mẫu số liệu là: R = 19 – 1 = 18.
• Cỡ mẫu n = 10 là số chẵn nên giá trị tứ phân vị thứ hai là $Q_{2}$ = $\frac{1}{2}$(9 + 10) = 9,5.
• Tứ phân vị thứ nhất là trung vị của mẫu: 1; 2; 5; 5; 9. Do đó, $Q_{1}$ = 5.
• Tứ phân vị thứ ba là trung vị của mẫu: 10; 10; 15; 15; 19. Do đó $Q_{3}$ = 15.
• Khoảng tứ phân vị của mẫu là: $\Delta_{Q}$ = 15 – 5 = 10.

Vận dụng 1:  Dưới đây là bảng số liệu thống kê của Biểu đồ nhiệt độ trung bình các tháng trong năm 2019 của hai tỉnh Lai Châu và Lâm Đồng (được đề cập đến ở hoạt động khởi động của bài học).

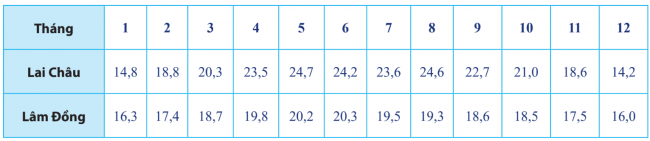
a. Hãy tìm khoảng biến thiên và khoảng tứ phân vị của nhiệt độ trung bình mỗi tháng của tỉnh Lai Châu và Lâm Đồng.

b. Hãy cho biết trong một năm, nhiệt độ ở địa phương nào ít thay đổi hơn.

Hướng dẫn giải:

a. Sắp xếp nhiệt độ trung bình mỗi tháng của tỉnh Lai Châu theo thứ tự không giảm, ta được:

14,2; 14,8; 18,6; 18,8; 20,3; 21,0; 22,7; 23,5; 23,6; 24,2; 24,6; 24,7

• Khoảng biến thiên của nhiệt độ trung bình mỗi tháng của tỉnh Lai Châu là: 24,7 – 14, 2 = 10,5
• Cỡ mẫu n = 12 là số chẵn nên giá trị tứ vị phân thứ hai là $Q_{2}$ = $\frac{1}{2}$(21,0 + 22,7) = 21,85.
• Tứ phân vị thứ nhất là trung vị của mẫu: 14,2; 14,8; 18,6; 18,8; 20,3; 21,0. Do đó $Q_{1}$ = $\frac{1}{2}$(18,6 + 18,8) = 18,7
• Tứ phân vị thứ ba là trung vị của mẫu: 22,7; 23,5; 23,6; 24,2; 24,6; 24,7. Do đó $Q_{3}$ = $\frac{1}{2}$(23,6 + 24,2) = 23,9
• Khoảng tứ phân vị của nhiệt độ trung bình mỗi tháng của tỉnh Lai Châu là: $\Delta_{Q}$ = 23,9 – 18,7 = 5,2.

Sắp xếp nhiệt độ trung bình mỗi tháng của tỉnh Lâm Đồng theo thứu tự không giảm, ta được: 

16,0; 16,3; 17,4; 17,5; 18,5; 18,6; 18,7; 19,3; 19,5; 19,8; 20,2; 20,3

• Khoảng biên thiên của nhiệt độ trung bình mỗi tháng của tỉnh Lâm Đồng là R = 20,3 – 16,0 = 4,3
• Cỡ mẫu n = 12 là số chẵn nên giá trị tứ vị phân thứ hai là $Q_{2}$ = $\frac{1}{2}$(18,6 + 18,7) = 18,65.
• Tứ phân vị thứ nhất là trung vị của mẫu: 16,0; 16,3; 17,4; 17,5; 18,5; 18,6. Do đó $Q_{1}$ = $\frac{1}{2}$(17,4 + 17,5) = 17,45.
• Tứ phân vị thứ ba là trung vị của mẫu: 18,7; 19,3; 19,5; 19,8; 20,2; 20,3. Do đó $Q_{3}$ = $\frac{1}{2}$(19,5 + 19,8) = 19,65.
• Khoảng tứ phân vị của nhiệt độ trung bình mỗi tháng của tỉnh Lâm Đồng là: $\Delta_{Q}$ = 19,65 – 17,45 = 2,2.

b. Nhận thấy khoảng biến thiên và khoảng tứ phân vị của nhiệt độ trung bình mỗi tháng của tỉnh Lâm Đồng nhỏ hơn tỉnh Lai Châu nên nhiệt độ ở Lâm Đồng ít thay đổi trong một năm hơn.

Thực hành 2:  Hãy tìm giá trị ngoại lệ của mẫu số liệu: 37; 12; 3; 9; 10; 9; 12; 3; 10.

Hướng dẫn giải:

Sắp xếp số liệu trong mẫu theo thứ tự giảm dần là: 3; 3; 9; 9; 10; 10; 12; 12; 37.

• Cỡ mẫu n = 9 là số lẻ nên giá trị tứ phân vị thứ hai là: $Q_{2}$ = 10.
• Tứ phân vị thứ nhất là trung vị của mẫu: 3; 3; 9; 9. Do đó $Q_{1}$ = $\frac{1}{2}$(3 + 9) = 6
• Tứ phân vị thứ hai là trung vị của mẫu: 10; 12; 12; 37. Do đó $Q_{3}$ = 12
• Khoảng tứ phân vị của mẫu là: $\Delta_{Q}$ = 12 – 6 = 6

Xét $Q_{3}$ + 1,5$\Delta_{Q}$ = 12 + 1,5. 6 = 21 và $Q_{1}$ – 1,5$\Delta_{Q}$ = 6 – 1,5. 6 = -3

Vậy mẫu có một giá trị ngoại lệ là 37.

2. PHƯƠNG SAI VÀ ĐỘ LỆCH CHUẨN

Khám phá 2:  Hai cung thủ A và B đã ghi lại kết quả của từng lần bắn của mình ở bảng sau:

a. Tính kết quả trung bình của mỗi cung thủ trên.

b. Cung thủ nào có kết quả các lần bắn ổn định hơn?

Hướng dẫn giải:

a. Kết quả trung bình của cung thủ A là: $\frac{1}{10}$(8 + 9 + 10 + 7 + 6+ 10 + 6 + 7 + 9 + 8) = 8

    Kết quả trung bình của cung thủ B là $\frac{1}{10}$(10 + 6 +8 + 7 + 9 + 9 + 8 + 7 + 8 + 8) = 8

b. Cung thủ B có các kết quả các lần bắn ổn định hơn.

Vận dụng 2:  Bảng dưới đây thống kê tổng số giờ nắng trong năm 2019 theo từng tháng được đo bởi hai tram quan sát khí tượng đặt ở Tuyên Quang và Cà Mau.

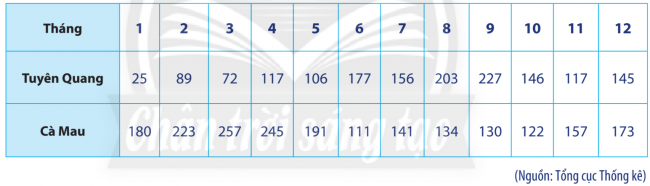
a. Hãy tính phương sai và độ lệch chuẩn của dữ liệu từng tỉnh

b. Nhận xét về sự thay đổi tổng số giờ nắng theo từng tháng ở mỗi tỉnh.

Hướng dẫn giải:

a.

• Trung bình số giờ nắng ở Tuyên Quang là: 

$\bar{x_{1}}$ = $\frac{1}{12}$(25 + 89 + 72 + 117 + 106 + 177 + 156 + 203 + 227 + 146 + 117 + 145) $\approx$ 131,7

• Trung bình số giờ nắng ở Cà Mau là:

$\bar{x_{2}}$ = $\frac{1}{12}$(180 + 223 + 257 + 245 + 191 + 111 + 141 + 134 + 130 + 122 + 157 + 173) = 172

• Phương sai của số giờ nắng ở Tuyên Quang là:

$S_{1}^{2}$ = $\frac{1}{12}$($25^{2}$ + $89^{2}$ + $72^{2}$ + $117^{2}$ + $106^{2}$ + $177^{2}$ + $156^{2}$ + $203^{2}$ + $227^{2}$ + $146^{2}$ + $117^{2}$ + $145^{2}$) – $131,7^{2}$ $\approx$ 2912,4

• Độ lệch chuẩn của số giờ nắng ở Tuyên Quang là: $S_{1}$ = $\sqrt{S_{1}^{2}}$ = $\sqrt{2912,4}$ $\approx$ 54.
• Phương sai của số giờ nắng ở Cà Mau là:

 $S_{2}^{2}$ = $\frac{1}{12}$($180^{2}$ + $223^{2}$ + $257^{2}$ + $245^{2}$ + $191^{2}$ + $111^{2}$ + $141^{2}$ + $134^{2}$ + $130^{2}$ + $122^{2}$ + $157^{2}$ + $173^{2}$) – $172^{2}$ = 2183

• Độ lệch chuẩn của số giờ nắng ở Cà Mau là: $S_{2}$ = $\sqrt{S_{2}^{2}}$ = $\sqrt{2183}$ $\approx$ 46,7.

b. Nhìn chung:

• Ở Tuyên Quang, tổng số giờ nắng có xu hướng tăng dần từ đầu năm đến giữa năm và giảm dần về cuối năm.
• Ở Cà Mau, tổng số giờ nắng giảm dần từ đầu năm đến giữa năm và tăng dần về cuối năm.

===========
Chuyên mục: Học Toán lớp 10 – Chân trời