Toán thực tế THPT 2015

Anh Bình muốn vay ngân hàng $200$ triệu đồng theo phương thức trả góp (trả tiền vào cuối tháng) với lãi suất $0,75\%$ / tháng. Hỏi hàng tháng anh Bình phải trả số tiền là bao nhiêuđể sau đúng hai năm thì trả hết nợ ngân hàng (Đơn vị tính là triệu đồng và kết quả làm tròn đến hàng phần trăm)

Ngày 06/06/2025 Thuộc chủ đề:Toán thực tế THPT 2015 Tag với:Toán 12 thực tế

ĐỀ BÀI: Anh Bình muốn vay ngân hàng $200$ triệu đồng theo phương thức trả góp (trả tiền vào cuối tháng) với lãi suất $0,75\%$ / tháng. Hỏi hàng tháng anh Bình phải trả số tiền là bao nhiêuđể sau đúng hai năm thì trả hết nợ ngân hàng (Đơn vị tính là triệu đồng và kết quả làm tròn đến hàng phần trăm) LỜI GIẢI ĐÁP ÁN 9,14 Gọi $q$ (triệu đồng) là số tiền hàng tháng anh Bình … [Đọc thêm...] vềAnh Bình muốn vay ngân hàng $200$ triệu đồng theo phương thức trả góp (trả tiền vào cuối tháng) với lãi suất $0,75\%$ / tháng. Hỏi hàng tháng anh Bình phải trả số tiền là bao nhiêuđể sau đúng hai năm thì trả hết nợ ngân hàng (Đơn vị tính là triệu đồng và kết quả làm tròn đến hàng phần trăm)

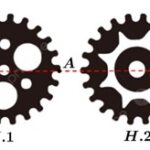
Hình vẽ dưới đây là hai bánh răng của một động cơ, chúng có cùng kích thước. Khi động cơ hoạt động, hai bánh răng quay đều cùng chiều. Biết tốc độ quay của bánh răng ở hình 2 gấp đôi tốc độ quay của bánh răng ở hình 1 và phương trình biểu thị độ cao của điểm $A$ ở bánh răng thứ nhất là $h=2R+R\sin\left(\dfrac{\pi}{5}t\right)$(trong đó $R$ là bán kính bánh răng, $t$ là thời gian tính bằng giây, $h$ là độ cao của điểm $A$). Giả sử tại thời điểm bắt đầu khởi động, hai điểm $A$ và $B$ có độ cao bằng nhau.

Ngày 06/06/2025 Thuộc chủ đề:Toán thực tế THPT 2015 Tag với:Toán 12 thực tế

ĐỀ BÀI: Hình vẽ dưới đây là hai bánh răng của một động cơ, chúng có cùng kích thước. Khi động cơ hoạt động, hai bánh răng quay đều cùng chiều. Biết tốc độ quay của bánh răng ở hình 2 gấp đôi tốc độ quay của bánh răng ở hình 1 và phương trình biểu thị độ cao của điểm $A$ ở bánh răng thứ nhất là $h=2R+R\sin\left(\dfrac{\pi}{5}t\right)$(trong đó $R$ là bán kính bánh răng, $t$ là … [Đọc thêm...] vềHình vẽ dưới đây là hai bánh răng của một động cơ, chúng có cùng kích thước. Khi động cơ hoạt động, hai bánh răng quay đều cùng chiều. Biết tốc độ quay của bánh răng ở hình 2 gấp đôi tốc độ quay của bánh răng ở hình 1 và phương trình biểu thị độ cao của điểm $A$ ở bánh răng thứ nhất là $h=2R+R\sin\left(\dfrac{\pi}{5}t\right)$(trong đó $R$ là bán kính bánh răng, $t$ là thời gian tính bằng giây, $h$ là độ cao của điểm $A$). Giả sử tại thời điểm bắt đầu khởi động, hai điểm $A$ và $B$ có độ cao bằng nhau.